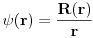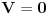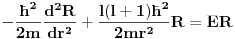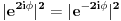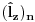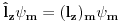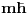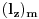[ petarm @ 21.09.2008. 14:29 ] @
|
[ petarm @ 24.09.2008. 08:40 ] @
ZAD
Sistem se nalazi u stanju opisanom fjom 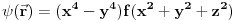 . Merimo vrednosti . Merimo vrednosti  -komponente momenta impulsa -komponente momenta impulsa 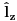 . Koje vrednosti mozemo dobiti kao rezultate pojedinacnih eksperimenata, a kolika ce biti srednja vrednost velikog broja merenja (ocekivana vrednost)? . Koje vrednosti mozemo dobiti kao rezultate pojedinacnih eksperimenata, a kolika ce biti srednja vrednost velikog broja merenja (ocekivana vrednost)? RES: Izrazim talasnu fju u sfernim koordinatama kao i operator  komponente orbitalnog momenta. I onda sa tim operatorom komponente orbitalnog momenta. I onda sa tim operatorom 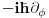 oddelujem na oddelujem na 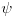 i dobijem nesto sto mnozi i dobijem nesto sto mnozi 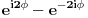 puta nesto... I odatle zakljucujem da je puta nesto... I odatle zakljucujem da je 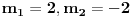 i stoga i stoga 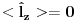 . . Jel ovo OK.? Moze li obrazlozenje ovog? [ tomkeus @ 27.09.2008. 20:01 ] @
Citat: Da. Citat: petarm: Kako pod b)? Skalarni proizvod stanja koje odgovara energiji 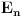 sa stanjem sa stanjem  Citat: petarm: ZAD Izrazim talasnu fju u sfernim koordinatama kao i operator  komponente orbitalnog momenta. I onda sa tim operatorom komponente orbitalnog momenta. I onda sa tim operatorom 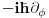 oddelujem na oddelujem na 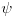 i dobijem nesto sto mnozi i dobijem nesto sto mnozi 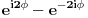 puta nesto... I odatle zakljucujem da je puta nesto... I odatle zakljucujem da je 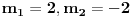 i stoga i stoga 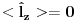 . . Jel ovo OK.? Moze li obrazlozenje ovog? Jeste. Ono što prvo moraš uraditi je da razložiš 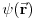 na svojstvene vektore operatora na svojstvene vektore operatora 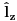 , a to su , a to su 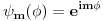 što je lagano jer što je lagano jer 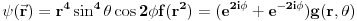 . Dakle, stanje je linearna kombinacija svojstvenih stanja za m=2 i m=-2, pri čemu uz oba stanja stoje jednaki koeficijenti, što znači da će se očekivana vrednost u ovom stanju anulirati jer . Dakle, stanje je linearna kombinacija svojstvenih stanja za m=2 i m=-2, pri čemu uz oba stanja stoje jednaki koeficijenti, što znači da će se očekivana vrednost u ovom stanju anulirati jer 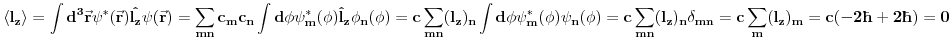 [Ovu poruku je menjao tomkeus dana 27.09.2008. u 21:20 GMT+1] [ petarm @ 27.09.2008. 20:36 ] @
[ tomkeus @ 28.09.2008. 11:20 ] @
[ petarm @ 28.09.2008. 12:31 ] @
Ok.
[ petarm @ 28.09.2008. 14:04 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|