[ Nedeljko @ 02.10.2008. 13:17 ] @
Jel zadaci nisu interesantni ili niko ne ume da ih resi?
[ Nedeljko @ 03.10.2008. 08:26 ] @
Da li ovo ikoga uopšte zanima ili da ne objavljujem rešenja?
[ petarm @ 03.10.2008. 08:54 ] @
Objavi resenja! Ocigledno trenutno nema previse zainteresovanih, ali bice sigurno za dan. dva...
[ Nedeljko @ 03.10.2008. 13:31 ] @
Možda ako se bar neko javi da je zainteresovan za rešenja.
[ petarm @ 04.10.2008. 09:37 ] @
Meni bi bilo zanimljivo da vidim resenja posto ne znam da resim ove zadatke. Ako su relativno detaljna naravno?
[ Nedeljko @ 04.10.2008. 18:41 ] @
1. Neka je
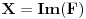
i
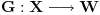
definisano sa
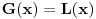
. Poznata formula
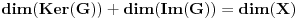
(zbir dienzija jezgra i slike jednak je dimenziji domena linearnog preslikavanja) daje
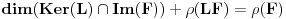
. Obzirom da je
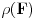
po pretpostavci konačno, konačni su i
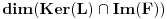
i
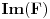
, pa je
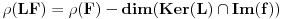
.
2. Iz konačnosti
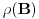
sledi konačnost
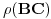
, pa je
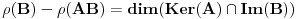
,
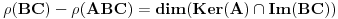
.
Obzirom da je
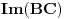
potprostor od
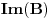
, važi
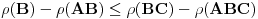
, odakle sledi tvrđenje.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.