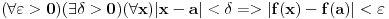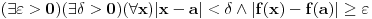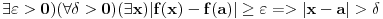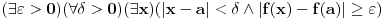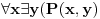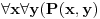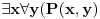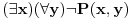Ja bi negaciju odradio ovako:



_{[Ovu poruku je menjao h4su dana 04.10.2008. u 14:45 GMT+1]}

mislim da ti nije dobro, ti si samo izmenjao kvantifikatore i p=>q zamenio sa (ne q)=>(ne p). imaj u vidu da je (p=>q)<=>(ne q=>ne p) a ti si trebao da negiras moju implikaciju a to nisi uradio kako treba pa ne smes da diras kvantifikatore dok ne utvrdis sta treba da se desi sa p i q.

Prilikom negacije prevrćemo svaki kvantifikator (a ne samo prvi). Dakle, negacija glasi:

jasno mi je, vidim i gde si stavio zagradu (nisam bio siguran da li je neki od kvantifikatora unutar zagrade. danke

U pravu si za drugi dio:negirano( p implicira q) ekvivalento je p i ne q.E sad i mene interesuje:


Neka imamo:
.

Sljedeci iskazi nisu tacni:

.
.

Sta bi bila negacija ? Ne postoji x tako da za svako y P(x,y) ?

Negacija: .

Hvala,i ja pitam gluposti.

e sad imam pitanje.... da li je neprekidna... :D od jednih cujem da jeste od jednih da nije.... jedni kazu da je prekidna u 0,a drugi kazu da u nula ne pripada domenu funkcije, ko je sad u pravu??

Funkcija 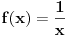je neprekidna funkcija. Nula ne pripada domenu funkcije, te u toj tacki ne ispitujemo neprekidnost.

Uostalom, imas malu diskuciju na http://www.elitesecurity.org/t427675-1#3020760