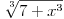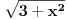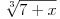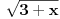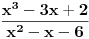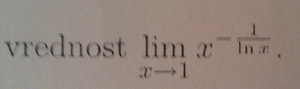[ kavens @ 05.10.2008. 15:13 ] @
|
[ peddja_stankovic @ 05.10.2008. 15:31 ] @
gore oduzmi 4 i dodaj 4 pa rastavi na 2 limesa (two in one), prvi racionalisi na razliku kubova a drugi na razliku kvadrata.
[ kavens @ 05.10.2008. 15:41 ] @
Hvala na odgovoru,ne razumem kako 2u1 ?
[ peddja_stankovic @ 05.10.2008. 16:24 ] @
[ kavens @ 05.10.2008. 16:50 ] @
Hvala
[ kavens @ 05.10.2008. 18:38 ] @
[ Nedeljko @ 05.10.2008. 19:00 ] @
Ovakvi limesi se najlakše rešavaju Lopitalovim pravilom.
[ kavens @ 05.10.2008. 19:25 ] @
Citat: Nedeljko: Ovakvi limesi se najlakše rešavaju Lopitalovim pravilom. Sa ovim se jos nisam upoznao :) [ peddja_stankovic @ 05.10.2008. 19:36 ] @
@kavens
isto ko malopre, oduzmi 2 i dodaj 2 dobijas rezultat -1/6 @Nedeljko zavisi koja je skola, srednja, visa ili fax i da li im je dozvoljeno da koriste lopitalovu teoremu [ kavens @ 05.10.2008. 20:24 ] @
@peddja_stankovic
u resenju je rezultat -1/4 [ Daniel011 @ 05.10.2008. 23:57 ] @
Tačno je rešenje -1/4. Ako si kod ovakve vrste zadataka u nedoumici koji broj treba u brojiocu da dodaš i da oduzmeš pri rastavljanju na dva limesa, možeš slobodno da dodaš i da oduzmeš n, a posle ćeš u toku rešavanja zadatka i sam videti koliko to n treba da bude i kojim brojem ga je potrebno zameniti, kako bi bilo moguće skraćivanje faktora.
[ peddja_stankovic @ 06.10.2008. 06:00 ] @
oduzimas onaj broj koji se dobija na sledeci nacin; zameni se broj kome tezi x u prvi koren, e to je carobni broj koji se oduzima i dodaje. na primer zameni se x=1 u treci koren ix x+7 pa se dobije treci koren iz 8 a to je 2
[ kavens @ 06.10.2008. 12:33 ] @
Jos jednom hvala
[ peddja_stankovic @ 06.10.2008. 13:55 ] @
ja dobih -1/6 a i mathcad -1/6. sad vi vidite na koga da se kladite
http://i262.photobucket.com/albums/ii98/pedjasta/S7301479.jpg [ Daniel011 @ 06.10.2008. 14:09 ] @
[ peddja_stankovic @ 06.10.2008. 14:18 ] @
pazi majku mu @%$#&*|\
trebalo je zoomiram sliku [ Daniel011 @ 06.10.2008. 15:49 ] @
Da, zaista se ne vidi dok se slika ne zumira.
Ljudi, koristite taj (La)TeX, nije uopšte teško naučiti ga: http://www.elitesecurity.org/t35291-Sve-La-TeX-na-ovom-forumu [ jovana1995 @ 13.11.2012. 22:30 ] @
moze pomoc oko ovog zadatka??
lim x(na 3) +2( x na 2) -2x-1/x(na 2) +2x-3 x→1 [ Sonec @ 13.11.2012. 22:32 ] @
Potrudi se da malo lepse zapises, posto ovako nije najcitljivije.
[ jovana1995 @ 13.11.2012. 22:39 ] @
jao ne znam bas ...ne razumem se najbolje...ne znam kako da upisem stepene :(
[ Sonec @ 13.11.2012. 22:43 ] @
Recimo da si mislila na ovo
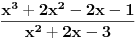 . Sta radimo kad vidimo (ako imamo problem da direktno uvrstimo . Sta radimo kad vidimo (ako imamo problem da direktno uvrstimo 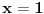 ) ovakav izraz? Pa rastavimo brojilac i imenilac. Primeti da i brojilac i imenilac se anuliraju u 1, pa prema Bezuovom stavu vazi da.... Rastavi brojilac i imenilac na cinioce, nesto ce se pokratiti i fakticki si zavrsila. ) ovakav izraz? Pa rastavimo brojilac i imenilac. Primeti da i brojilac i imenilac se anuliraju u 1, pa prema Bezuovom stavu vazi da.... Rastavi brojilac i imenilac na cinioce, nesto ce se pokratiti i fakticki si zavrsila.[ miki069 @ 13.11.2012. 22:47 ] @
1. Imenilac izjednačiš sa nulom i nađeš X1 i X2.
To će biti X1=1 i X2=-3. Onda ga napišeš u obliku proizvoda (X-1)*(X+3). 2. Brojilac podeliš sa (X-1) i biće deljiv bez ostatka (ostatak = nula). Napišeš ga u obliku proizvoda (X-1)*(polinom drugog stepena dobijen kao rezultat deljenja). 3. Skratiš razlomak sa (X-1) i u dobijeni razlomak zameniš X=1. 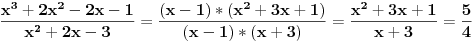 [ jovana1995 @ 13.11.2012. 22:48 ] @
lim x^3 +2x^2 -2x-1
x→1 —————————— x^2 +2x-3 nadam se da je bolje sad ? :D [ jovana1995 @ 13.11.2012. 22:51 ] @
a mozes da mi uradis zadatak...treba mi za sutra... puci ce mi glava.. bila bih ti zahvalna puno :)
[ jovana1995 @ 13.11.2012. 22:55 ] @
hvala,hvala punooo... punoooo
[ Sonec @ 13.11.2012. 22:59 ] @
[ miki069 @ 13.11.2012. 23:00 ] @
[ kovac88 @ 16.12.2012. 17:23 ] @
[ kovac88 @ 16.12.2012. 17:46 ] @
Ne kazuje mi se nazalost :(
[ kovac88 @ 16.12.2012. 18:00 ] @
Ne bi mi to palo na pamet...hvala :)
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|