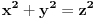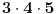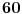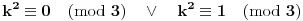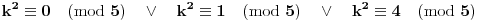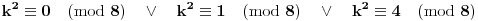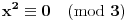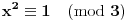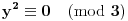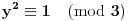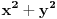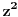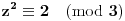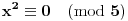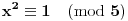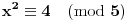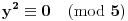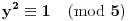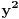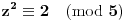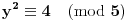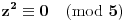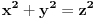
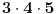
Ako dokažemo da je među brojevima , i koji zadovoljavaju zadati uslov jedan od njih uvek deljiv sa , jedan uvek deljiv sa , a jedan uvek deljiv sa , dokazali smo da je njihov proizvod uvek deljiv sa , tj sa .
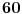
Možeš se poslužiti osobinama kvadrata prirodnog broja, po kojima je:





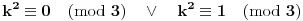
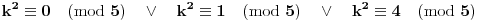
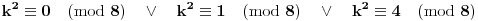
(Sve ovo se takođe može dokazati; ako bude potrebno, napisaću i taj dokaz.)

Sada posmatraš zadati izraz


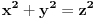
Dokaz da je jedan od brojeva , ili deljiv sa :
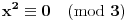
Postoje dve mogućnosti: jedna je , a druga je .
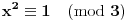
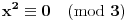
U slučaju da je , samim tim imamo jedan broj () koji je deljiv sa .
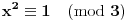
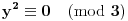
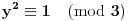
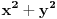
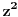
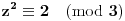
U slučaju da je , mora biti , jer ako bi bilo , tada bi , tj. bilo , što je nemoguće.
Ako je kvadrat nekog broja deljiv sa , onda je i sam taj broj deljiv sa (i ovo se jednostavno dokazuje).

Na sličan, samo na malo složeniji način, se dokazuje i za deljivost sa i sa . S tim da, ako je kvadrat nekog broja deljiv sa , tada je i taj broj deljiv sa . Međutim, da bismo dokazali da je neki broj deljiv sa , nije dovoljno dokazati da je njegov kvadrat deljiv sa (kontraprimer: broj ), nego moramo dokazati da je kvadrat tog broja deljiv sa . Zbog toga sam gore napisao osobine kvadrata za module , i .

Pokazaću još dokaz za modul , a gotovo identično se radi i za modul .

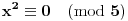
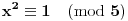
Postoje tri mogućnosti: jedna je , druga je , a treća je .
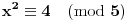
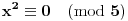
U slučaju da je , samim tim imamo jedan broj () koji je deljiv sa 5.
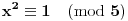
U slučaju da je , imamo tri podslučaja.
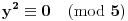
- Prvi je da je , pa opet imamo jedan broj koji je deljiv sa .
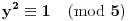
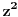
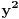
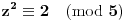
- Drugi podslučaj je da je , tada bi , koji predstavlja zbir i , bio , što odbacujemo kao nemoguć slučaj.
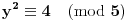
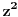
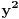
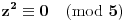
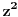
- Treći podslučaj je da je , tada bi , koji predstavlja zbir i , bio , tako da je u ovom slučaju deljivo sa .
Identičan je postupak i za slučaj da je .
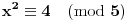