[ Shadowed @ 11.11.2003. 01:44 ] @
| Ne vidim razlog zasto ne bi mogao ali da proverim. Dakle moze li elemnt skupa biti sam taj skup? |
|
[ Shadowed @ 11.11.2003. 01:44 ] @
[ vlayceh @ 11.11.2003. 08:21 ] @
Ne, skup ne moze sadrzati samog sebe.
Teorija skupova je aksiomatski zasnovana, i na osnovu jedne od tih aksioma se izvodi dato tvrdjenje. Nazalost, zaboravio sam ime te aksiome. [ noviKorisnik @ 11.11.2003. 09:59 ] @
Ako je jedan skup definisan kao skup svih skupova, po toj definiciji mora sadržati i sebe.
[ Ivan Dimkovic @ 11.11.2003. 10:30 ] @
Citat: Ako je jedan skup definisan kao skup svih skupova, po toj definiciji mora sadržati i sebe. Da, ali time ulazis u paradoks - def: X skup svih skupova koji nemaju sebe kao podskup Ako kazemo da X pripada X, to je kontradikcija, jer je X po definiciji skup svih skupova koji ne sadrze sami sebe - a ovde upravo sadrzi samog sebe Ako kazemo da X ne pripada X, ispada da X zadovoljava definiciju, i X pripada X... sto je opet nemoguce Mislim da te zanima Russel: http://plato.stanford.edu/entries/russell-paradox/ http://www.utm.edu/research/iep/p/par-russ.htm http://www.cut-the-knot.org/selfreference/russell.shtml Ovakvih paradoksa ima dosta, problem sa skupovima je samo manifestacija osobine svih formalnih logickih sistema. [ noviKorisnik @ 11.11.2003. 12:26 ] @
Ne vidim vezu s Raselovim paradoksom, voleo bih da je vidim.
Pomenuo sam skup svih skupova, bez neke osobine za selekciju u smislu pripada li neki skup tom skupu, ili ne. Ako je nešto skup, to znači da pripada ovom skupu. Opet, ako ovakav skup jeste skup, onda je i svoj element. Istina, sve miriše na neki paradoks, ali bih voleo da vidim šta ruši postavku. [ Shadowed @ 11.11.2003. 13:29 ] @
Ovo sto je rekao noviKorisnik bi treblo da znaci da moze sadrzati.
Inace, povod sto sam to uopste i pitao jeste upravo taj paradoks. Procitao sam pre dosta vremena o njemu pa nisam bio siguran da li je uopste moguce da skup sadrzi samog sebe. Sad ostaje pitanje sta matematika "kaze" u vezi ovoga. Koliko znam matematika bi trebala da bude bez ikakvih paradoksa. [ byTer @ 11.11.2003. 13:53 ] @
Ako u toku nekog racuna dodjes da je podskup jednak skupu onda moze
[ srki @ 11.11.2003. 14:35 ] @
Citat: noviKorisnik: Ne vidim vezu s Raselovim paradoksom, voleo bih da je vidim. Ivan je samo na drugom primeru pokazao da iz definicije skupa ne sledi da takav skup postoji. Zato tvoja definicija nema nikakve veze sa problemom da li skup moze da sadrzi sam sebe. [ darkosos @ 11.11.2003. 15:04 ] @
Da, Raselov paradoks. On, i slicni, su razlog da se malo ostrije postave temelji teorije skupova, verovatno najznacajnije u Matematici.
Mozda pomogne A7. aksioma regularnosti, u ZF teoriji (Zermelo-Fraenkel) : 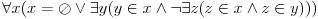 (izvor : "Hilbertovi problemi i logika" - Z. Mijajlovic, Z. Markovic i K. Dosen) Tj. skup x je ili prazan ili postoji element y koga on sadrzi i on je takav da ne postoji z sadrzan i u x i u y. Ako skup x sadrzi sebe, onda bi svi elementi skupa x bili i elementi njegovog elementa, tj. opet skupa x. Secam se da je neko pricao i o "skupnim" osobinama i o onima koje to nisu. Pa je receno da osobina "biti element samoga sebe" nije skupna jer bi tvrdjenje da takav skup postoji bilo kontradikcija. [ Ivan Dimkovic @ 11.11.2003. 15:33 ] @
Citat: Ne vidim vezu s Raselovim paradoksom, voleo bih da je vidim. Pomenuo sam skup svih skupova, bez neke osobine za selekciju u smislu pripada li neki skup tom skupu, ili ne. Ako je nešto skup, to znači da pripada ovom skupu. Opet, ako ovakav skup jeste skup, onda je i svoj element. Hmm... kako ne vazi, tvoja definicija nije dovoljna - jer vec imas paradoksalne slucajeve kakve sam ja naveo koji se krse sa definicijom. Dakle, ona vec pada ako je izaberemo da skup bude "skup skupova koji ne sadrze sami sebe" - znaci ne vazi za svaki skup "svih sadrzecih skupova", jer je u ovom konkretnom slucaju logicka kontradikcija. Citat: Tj. skup x je ili prazan ili postoji element y koga on sadrzi i on je takav da ne postoji z sadrzan i u x i u y. Ako skup x sadrzi sebe, onda bi svi elementi skupa x bili i elementi njegovog elementa, tj. opet skupa x. Secam se da je neko pricao i o "skupnim" osobinama i o onima koje to nisu. Pa je receno da osobina "biti element samoga sebe" nije skupna jer bi tvrdjenje da takav skup postoji bilo kontradikcija. Pa da, ideja je da se ogranici nacin odredjivanja pripadnosti i osobina. Mislim da je dosta radjeno na temu osobina skupova, http://www.utm.edu/research/iep/p/par-russ.htm Ali jos i dalje postoje debate oko najbolje teorije. U svakom slucaju i ova samo pokriva taj konkretni paradoks uvodjenjem jos nekih pravila :) Ali taj novi sistem ne oslobadja od svojih paradoksa :) [ Ivan Dimkovic @ 11.11.2003. 15:34 ] @
Citat: Sad ostaje pitanje sta matematika "kaze" u vezi ovoga. Koliko znam matematika bi trebala da bude bez ikakvih paradoksa. Ne, na zalost - upravo obrnuto, svaki formalni zatvoreni logicki sistem (principa matematica je jedan od njih) je osudjen bar na jedan paradoks dok ne uvedes dodatna pravila :) Mada su ljudi odavno prihvatili to kao nuzno zlo :) [ srki @ 11.11.2003. 15:44 ] @
Da napomenem da treba razlikovati paradoks i kontradikciju. Znam da znate razliku ali ipak moze da se desi da ne obratite paznju na nju. Aksimoe ne smeju da budu kontradiktorne ali paradoks moze da postoji.
[ Ivan Dimkovic @ 11.11.2003. 16:04 ] @
Da li je skup ujedno i svoj element?
Recimo, skup bubasvaba nije bubasvaba (nije svoj clan, nazovimo ovu vrstu U skupovi) Skup svih skupova sadrzi sebe (jeste svoj clan, nazovimo ovu vrstu V skupovi) U skupovi: svi skupovi koji nisu clanovi samih sebe V skupovi: svi skupovi koji jesu clanovi samih sebe Dakle, skup moze biti ili U tipa, ili V tipa, nikako i jednog i drugog u isto vreme. Niko nas ne sprecava da definisemo: Z: skup svih U skupova -- Skup svih skupva koji nisu clanovi samih sebe Pitanje: da li je skup Z skup U ili V tipa? :-) Ispada da skup Z nije ni U ni V skup :-) Kakav je to onda skup? :-) Evo jos malo paradoksa sa skupovima... 1. X je skup svih mogucih netacnih tvrdnji 2. Y je tvrdnja "Tvrdjenje Y je netacno" Da li je Y clan X ? Da bi se ovo dokazalo mora se ili dokazati da je Y podskup X, ili da Y nije podskup X - nikako oba tvrdjenja u isto vreme :) Pokusajte :) [ Shadowed @ 11.11.2003. 21:01 ] @
Pa ovde je koliko znam ona fora da Y nije iskaz jer su za definicuju iskaza uzeli da mora da bude odredivo da li je tacan ili ne (sto ovde nije slucaj - nema sanse da odredis da li je Y tacno ili ne).
[ Ivan Dimkovic @ 11.11.2003. 21:50 ] @
Citat: Pa ovde je koliko znam ona fora da Y nije iskaz jer su za definicuju iskaza uzeli da mora da bude odredivo da li je tacan ili ne (sto ovde nije slucaj - nema sanse da odredis da li je Y tacno ili ne). Tacnost nekog iskaza zavisi od pravila sistema (recimo aksioma, drugih tvrdjenja i sl). Primer sa Y skupom je logicki kontradiktoran odmah, medjutim prvi primer sa U i V tipovima skupova (kako sam ih ja nazvao) postaje paradoks tek kada se pokusa definicija Z skupa koji je skup svih U skupova. Problem je sto u svakom sistemu koji je kompletan mozes naleteti na bar jedan ovakav iskaz. Ovo je daleko veci problem nego sto izgleda na prvi pogled - onaj primer za "skup svih skupova" je samo jedna manifestacija istog problema. Za ljudski mozak (inteligenciju) ovo nije neki problem - jer covek vrlo lako uvidja da je nesto neresivo i uvodi nova pravila - dok kompjuterski program nije obdaren "izlazenjem iz sistema" :) off-topic, ali citao sam negde o nekom sistemu procene istinitosti na fuzzy logici koji se bas bavi efektnim zaobilazenjem beskonacnih rekurzija kao sto je ona sa tvrdjenjem Y :) [ darkosos @ 12.11.2003. 07:24 ] @
Hm, malo smo se zaleteli.
Sto se tice ovih primera sa skupovima, data aksioma izbacuje mogucnost da skup sadrzi sebe. Dalje, ne moze se skup formirati tako sto se napravi iskaz koji zovemo, recimo, osobina P(x), pa kazemo da je X = {x|P(x)}. Prvo, osobina P mora biti takva da se za svako x moze utvrditi da li vazi P(x) ili ne (to je vec Shadowed napomenuo). Drugo, familija formirana na ovakav nacin (tj svi koji imaju osobinu P) mora zadovoljavati aksiome teorije skupova, inace ne mozemo reci da je skup. Citat (isto kao gore): "... U takvoj situaciji javio se Ernst Zermelo 1908. godine jednim novim pristupom. Sustina njegove ideje je da skupovi koji se javljaju u matematici nisu zasnovani na intuiciji o podeli univerzuma svih mogucih objekata na dva dela (skup svih objekata koji imaju zadato svojstvo i skup svih onih koji ga nemaju), vec na predstavi o postepenoj, kumulativnoj izgradnji skupova polazeci od nekih unapred zadatih objekata - urelemenata (praelemenata), pri cemu neki skup moze kao elemente sadrzati samo skupove koji su izgradjeni pre njega. ... Ubrzo se pokazalo da urelementi nisu neophodni i da se svi skupovi koji se javljaju u matematici mogu izgraditi polazeci od praznog skupa." (bold i underline su moji) [ noviKorisnik @ 12.11.2003. 11:38 ] @
[ cedomir @ 12.11.2003. 12:20 ] @
prazan skup sadrži sam sebe :)
[ darkosos @ 12.11.2003. 16:18 ] @
[ srki @ 12.11.2003. 17:17 ] @
Citat: cedomir: prazan skup sadrži sam sebe :) Netacno! Da bi skup mogao da sadrzi sam sebe mora makar jedan od elemenata da bude skup. Evo ti npr jedan skup koji sadrzi i prazan skup kao element: {1, 5 , {}, 7, 9} [ noviKorisnik @ 13.11.2003. 07:49 ] @
Darko, nekako se vrtimo u krug.
x je skup koji sadrži skupove. Neka je y skup koji sadrži prirodne brojeve. Tada 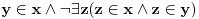 jer da postoji takav z, on bi u isto vreme morao biti i skup i prirodan broj (babe i žabe). jer da postoji takav z, on bi u isto vreme morao biti i skup i prirodan broj (babe i žabe).Mada, čini mi se da je ovo ipak moguće ako se uzme u obzir tvrdnja iz citata koji si naveo da "se svi skupovi koji se javljaju u matematici mogu izgraditi polazeci od praznog skupa". [ darkosos @ 13.11.2003. 13:40 ] @
Citat: Pa ne znam šta je sporno. Axioma zahteva mogućnost uspostavljanja hijerarhije. Ovaj tvoj primer sa skupom prirodnih brojeva se uklapa, jer si upotrebio deo axiome. Upravo je i napravljena da se ne bi brkale babe i žabe ;) [ noviKorisnik @ 13.11.2003. 15:55 ] @
Izgleda da sam zaboravio da navedem da se komentar odnosi na pitanje "Mozda eventualno da se doda da y nije prazan skup?"
Primer koji sam naveo ima neprazan y, a x i dalje zadovoljava axiom iako je definisan kao skup svih skupova i sadrži sebe. Dalje nisam pametan, iako se svuda lepo kaže da skup ne može da sadrži sebe. Potražio sam po netu pomenuti axiom regularnosti, recimo na adresi http://mathworld.wolfram.com/AxiomofFoundation.html stoji ova formulacija: 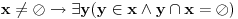 , a zanimljiva adresa je i http://planetmath.org/encyclopedia/AxiomOfFoundation.html , a zanimljiva adresa je i http://planetmath.org/encyclopedia/AxiomOfFoundation.htmlToliko, smorilo me pametovanje... [ Not now, John! @ 13.11.2003. 21:43 ] @
Ako se dobro sjećam, učio sam da svaki skup pored ostalog, sadrži prazan skup i samog sebe.
[ srki @ 13.11.2003. 22:32 ] @
Ovde se prica o elementu. Znaci da li element nekog skupa moze da bude taj skup. Ne misli se na podskup nego na element.
[ darkosos @ 14.11.2003. 06:48 ] @
@noviKorisnik
Ta formula je ekvivalentna onoj koju sam ja citirao. Ova tvoja koristi znak preseka, što se ne definiše samim axiomama. Ali je to upravo skraćenje one formule. Citat: Primer koji sam naveo ima neprazan y, a x i dalje zadovoljava axiom iako je definisan kao skup svih skupova i sadrži sebe. Dalje nisam pametan, iako se svuda lepo kaže da skup ne može da sadrži sebe. Hm, opet mi nije jasno. Al' 'ajd da ne tupimo više. Ovi linci što si dao su odlični. Malo sam procunjao, pa evo, ko hoće, mislim da je http://planetmath.org/encyclopedia/RussellsParadox.html prava stvar. Tu i kaže da je axioma regularnosti ona koja ne dozvoljava skup koji sadrži sam sebe (ipak imam dobar nos za ove stvari). A http://planetmath.org/encyclopedia/Class.html detaljnije govori o teoriji skupova. [ filmil @ 14.11.2003. 13:48 ] @
Ovaj, zna li iko šta se dešava sa Planetmath.org? Malo-malo pa nestane.
[ Nedeljko @ 17.04.2004. 02:32 ] @
Prvo, u Cermelo-Frankelovoj teoriji skupova (ZFC) jedini objekti su skupovi. Prirodni brojevi se takođe definišu kao određeni skupovi, npr. 0={}, 1={0}, 2={0,1}, 3={0,1,2}, tako da ne može biti nikakvog brkanja baba i žaba.
Primenom aksiome separacije se dokazuje da ne postoji skup svih skupova, jer bi se u protivnom (primenom aksiome separacije) iz njega izdvojio podskup onih skupova koji nisu sami sebi elementi i ako taj skup oynačimo sa A, onda bi A bio element od A ako i samo ako A nije element skupa A. Prazan skup ne pripada samom sebi jer nema elemenata. Ništa, pa ni prazan skup nije element praznog skupa. U aksiomi regularnosti stoji kvantifikator "postoji", a ne "za svaki" i ina bi se rečima mogla opisati kao "svaki neprazan skup je disjunktan sa barem jednim svojim elementom". Ako je A skup koji pripada samom sebi, onda je skup {A} neprazan i nije disjunktan sa svojim jedinim elementom A jer A pripada skupu A po pretpostavci, ali A pripada i skupu {A}, pa takav skup A ne postoji. Ne moraju se uvek prihvatiti sve aksiome ZFC sistema. Štaviše, često matematičari rade u teoriji ZF - sistem aksioma teorije skupova ZFC bez aksiome izbora (AC). Sa druge strane, često matematičari koriste i više aksioma od onih koje su nabrojane u sistemu ZFC. Tu posebno treba istaći kontinuum hipotezu (CH), generalisanu kontinuum hipotezu (GCH), aksiomu konstruktibilnosti (V=L), Martinovu aksiomu (MA), aksiomu determinisanosti (AD - samo bez aksiome izbora da bi sistem bio neprotivrečan. Obično ide uz aksiomu zavisnog izbora DC kao slabiju formu aksiome izbora), aksiomu projektivne determinisanosti (PD), konzistentnost sistema ZF (Con(ZF)) ili nekog drugog sistema aksioma, hipotezu o singularnim kardinalima (SCH), ili uz neku od hipoteza o velikim kardinalima ka što su slabo nedostižni (WINC), jako nedostižni (SINC), merljivi, Vudinovi i drugi. Tu treba pomenuti i hipoteze o kombinatornim tvrđenjima ka što su dijamant (  ), kvadrat, Suslinova hipoteza (SH) i Kurepina hipoteza (KH) i druge. Dakle, odgovor na ovo pitanje zavisi od toga u kom sistemu radimo. Da li uključujemo aksiomu regularnosti ili ne? ), kvadrat, Suslinova hipoteza (SH) i Kurepina hipoteza (KH) i druge. Dakle, odgovor na ovo pitanje zavisi od toga u kom sistemu radimo. Da li uključujemo aksiomu regularnosti ili ne?Postoje i teorije skupova u kojoj ima objekata koji nisu skupovi. Jedna od takvih je ZFA (Cermelo-Frankelova sa atomima). No, aksiome u tom slučaju menjaju svoj oblik. Moguća je i takva teorija skupova u kojoj ima skupova koji pripadaju sami sebi, i u njoj naravno ne važi aksioma regularnosti. [ zzzz @ 17.04.2004. 23:04 ] @
Čestitam Nedeljko!
Vidim da tu ima mnogo učenog,samo da priznam,ja nisam ništa shvatio. Ako možeš polako ponovo ovo izložiti za nas ostale... [ Nedeljko @ 18.04.2004. 01:06 ] @
Teorija skupova se izlaže aksiomatski. Najrasprostranjeniji sistem aksioma je ZFC. Teorija skupova se koristi i kao zasnivanje Matematike. Sistem ZFC na neki način opisuje "legalna" matematička sredstva. Ako se u dokazu koristi neko jače sredstvo, onda se mora istaći koje su dodatne hipoteze korišćene.
Aksioma separacije nam omogućava da iz bilo kog skupa izdvojimo podskup onih elemenata tog skupa koji imaju traženu osobinu izrazivu sredstvima predikatskog računa prvog reda na jeziku koji sadrži samo binarni relacijski simbol 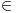 za pripadanje. Tako, ako bi A bio skup svih skupova, onda bismo mogli uočiti skup za pripadanje. Tako, ako bi A bio skup svih skupova, onda bismo mogli uočiti skup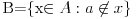 za koji bi važilo 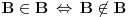 , što je kontradikcija. Dakle, Raselov paradoks u svetlu aksiomatske teorije skupova prestaje da bude paradoks i prelazi u teoremu da ne postoji skup svih skupova. , što je kontradikcija. Dakle, Raselov paradoks u svetlu aksiomatske teorije skupova prestaje da bude paradoks i prelazi u teoremu da ne postoji skup svih skupova.Prazan skup je skup bez elemenata. Ništa, pa ni prazan skup ne pripada praznom skupu. Aksioma regularnosti tvrdi da je svaki neprazan skup disjunktan sa barem jednim svojim elementom. Iz nje sledi da ne postoji skup koji bi pripadao samom sebi. Naime, ako je A skup za koji važi da 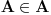 , onda bi skup {A} bio neprazan i njegov jedini element A ne bi bio disjunktan sa njim. Naime, zbog , onda bi skup {A} bio neprazan i njegov jedini element A ne bi bio disjunktan sa njim. Naime, zbog 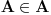 vaižlo bi vaižlo bi 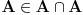 , odakle skupovi A i {A} ne bi bili disjunktni. , odakle skupovi A i {A} ne bi bili disjunktni.Skup {A} postoji z ma koji skup A po aksiomi para koja kaže da za ma koje a i b postoji skup čiji su jedini elementi a i b, tj. skup {a,b}, pa posebno kada je a=b=A dobijamo da mora da za ma koji skup A postoji skup {A}. Kao što rekoh, ZFC je podrazumevano "radno okruženje" ako se ne kaže drugačije, ali se može raditi i sa drugim sistemima aksioma. Recimo, nekada matematičari dokazuju teoreme koristeći dodatne aksiome (i tada moraju da napišu šta su dodatno koristili) dokazujući tvrđenja koja se pomoću ZFC aksioma ne mogu niti dokazati niti opovrgnuti. Te dodatne hipoteze su takođe neka tvrđenja koja ne zavise od aksioma ZFC. Time se na primer u okruženju ZFC ispituju uzajamne veze između takvih hipoteza. Jedno od takvih napoznatijih tvrđenja je kontinuum hipoteza (CH) koja glasi: "Ne postoji skup A takav da se niti skup R može 1-1 preslikati u skup A, niti da se skup A može 1-1 preslikati u skup N." Sa druge strane, često se ispituju posledice samo nekog dela aksiomatskog sistema ZFC. Obično se u tim slučajevima "žrtvuje" aksioma izbora, koja se često zamenjuje nekim slabijim oblicima, tj. tvrđenjima koja slede iz aksioma ZFC, ali uz ostale aksiome teorije skupova (bez aksiome izbora) nisu ekvivalentna aksiomi izbora, već predstavljanju njene slabije oblike. OK, kada možemo ispitivati posledice sistema ZFC bez aksiome izbora (koji se označava sa ZF), zašto ne bismo ispitivali posledice aksioma teorije skupova bez aksiome regularnosti? Tada nećemo moći da dokažemo da nijedan skup ne pripada samom sebi. Sa druge strane, za aksiomu regularnosti se obično kaže da predstavlaj aksiomu "tehničkog karaktera", tj. nijedno bitno matematičko tvrđenje ne zavisi od aksiome regularnosti, već samo marginalne zavrzlame kao što je nepostojanje skupa koji bi pripadao samom sebi. Nekada se aksioma izbora odbacuje i zamenjuje nekom od njenih slabijih oblika da bi se sistem aksioma proširio nekim važnim tvrđenjem koje protivreči sistemu aksioma ZFC. Dva najpoznatija takva tvrđenja su aksioma determinisanosti i Lebeg-merljivost svih podskupova skupa 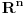 . .Nadam se da sam bio malo jasniji. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|