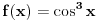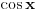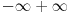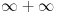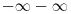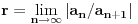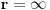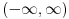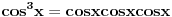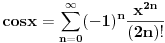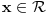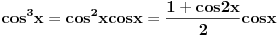Redove možeš da sabiraš i oduzimaš onda kada znaš da najviše jedan od njih divergira ili kada oba određeno divergiraju ka baskonačnosti, ali nemaš slučaj ili , već ili . Sa stepenim redovima možeš biti opušteniji, s tim da zbir razmatraš na preseku oblasti konvergencije.

Mozes li mi samo malo pojasniti ovo "Sa stepenim redovima možeš biti opušteniji, s tim da zbir razmatraš na preseku oblasti konvergencije"?
Nisam bas ucio teoriju, mrzelo me

za svaki stepeni red mora da se odredi interval konvergencije (-r,r) gde je radijus kovergencije

gde je i jos posebno da ispitas kovergenciju u krajevima intervala u -r i r. Lako se dobija da je pa ovaj red konvergira na





_{[Ovu poruku je menjao peddja_stankovic dana 25.10.2008. u 00:20 GMT+1]}

Kako je ,
Te se ustvari odmah lako uoci da red konvergira za

Probaj da izmnozis ova tri reda ako te ne mrzi? Cisto vezbe radi!

Lakse je naravno

Pa, kod stepenih redova je lako odrediti oblast konvergencije, ali u svakom slučaju treba da vodiš računa da zbir redova može da konvergira tamo gde oba reda divergiraju i tamo batali primenu takvog zbira.

hteo bih da dodam da je nekad lakse odrediti poluprecnik konvergencije preko korenskog kriterijuma umesto uporednog

po korenskom kriterijumu je r jednako 1 kroz limes superior kada n tezi beskonacno od n-tog korena opstog clana po apsolutnoj vrednosti