Imal kakvih rjesenja ?

Sto se tice prvog, to je standardan nacin resavanja.

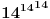
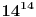
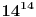
Sto se tice drugog, mogao si da kazes kako si ti radio. Treba najpre odrediti ostatje pri delenju sa 4 i 25, a onda od toga sklopiti rezultat. Rezultat je ocigledno deljiv sa 4. 14 je uzajamno prosto sa 25, pa mozes primeiti Ojlerovu teoremu. No onda treba odrediti ostatak pri delenju broja sa 20, odnosno sa 4 i sa 5. Broja je svakako deljiv sa 4, a posto je 14 uzajamno prosto sa 5, opet primenjujes Ojlerovu teoremu. 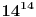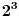Ostatak pri delenju 14 sa 4 je 2, odnosno 14 sa 5 je 3, pa je po modulu 5 kongruentno sa , odnosno sa 3. 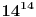Odatle sledi da je kongruentno po modulu 20 sa 8. 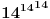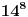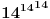Zbog toga je kongruentno po modulu 25 sa odnosno sa 6, a kako je deljivo sa 4, rezultat je 56.

Pozdrav,Nedeljko nista bez tebe :D.Hvala na odgovoru, mislio sam mozda postoji neka druga fora na koju se moze uraditi prvi a drugi sam radio ovako:

kongruentno sa 6 po modulu 10 pa sam onda posmatrao po modulu 100.

Imam i ja neke omaske. 14¹⁴ je po modulu 20 kongruentno sa 16, pa je samim tim rezultat 36. No, nema veze. Gresis u pristupu jer znaci , a ne .

Eh,ovako







slijedi
........
........
........
........




pa na osnovu posljedice kineske teoreme o ostacima

Dobro je.