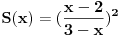Pa, to nisu stepeni redovi.

Nisu stepeni redovi, ali bi se moglo raditi konvergencija reda u zavisnosti od parametra x, pa tako dobiti oblast konvergencije (skup x-ova za koje red konvergira). Jel se na to mislilo?

Vidi kad je (x-1)/(x+1) pozitivno pa koristi Dalamberov kriterijum za konv. redova sa pozitivnim clanovima a tamo gde je (x-1)/(x+1) negativno koristi recimo Lajbnicov kriterujum za alternativne redove.

Ma kako bre nisu to stepeni redovi??
Kod mene u knjizi stoji naslov stepeni (potencijalni) redovi.

Evo kako se radi primer koji sam gore naveo:
Znaci naci sumu reda: :
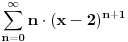
Nadje se poluprecnik konvergencije:


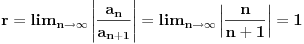
Poluprecnik konv. je 1 a centar konvergencije je 2 iz ovoga sledi da je x u intervalu izmedju 1 i 3.
Sad treba proveriti za x=1 i za x=3 da li red konvergira:

x=1:
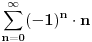
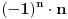
iz ovoga se vidi da opsti clan () ne tezi nuli pa red divergira
x=3:
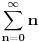
takodje opsti clan ne tezi nuli pa red divergira

Znaci red je definisan za

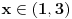
Neka je
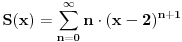
Izvrsi se smena

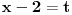
Neka je
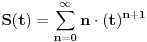
Posto je prvi clan ove sume jednak nuli tada se ova suma moze zapisati i:

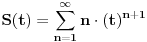
Sad se resava ovaj red:


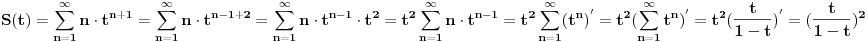
Iz ovoga sledi da je:

Pa nista, uvedi smenu (x-1)/(x+1)=t i onda ti se zadatak svodi na prethodni primer. dobijes -1<t<1 odnosno -1<(x-1)/(x+1)<1 pa ako nisam pogresio resenje je x>0 oblast konvergencije i onda nema centar konvergencije. Sto se tice sumiranja, u rezultat (t/(1-t))^2 zameni t, sredi i dobijes sto treba. Slicno ovaj drugi primer. Ono gore napisi kao [((x-1)^2)^n]*(x-1)^2 a ono dole kao [(x^2+1)^n]*(x^2+1)^3 pa ti bude t=[(x-1)^2]/(x^2+1) a ono preostalih x-ova izvuci ispred sume itd...

Da, i morao bi malo sa indeksima sume da se poigras jer nije samo Copy/Paste. Ako ne budes mogao sam, videcu kad budem imao vremena da uradim ceo zadatak



_{[Ovu poruku je menjao peddja_stankovic dana 01.11.2008. u 09:26 GMT+1]}

Definitivno nije reč o stepenom redu, ali se zadatak određivanja oblasti konvergencije jednostavnom smenom svodi na stepeni, kao što je Peđa to pokazao. To je drugo. No, pojam centra oblasti konvergencije je tu malo sporan, jer se definiše samo za stepene redove.

I ja se slazem sa Nedeljkom. Ovo je funkcionalni red



i uz funkcionalni red ide oblast konvergencije funkcionalnog reda a radijus konvergencije i interval konvergencije ide uz stepene redove



Nigde se u literaturi koju ja imam ne pominje cak ni pojam centar konvergencije mada je intuitivno jasno oo cemu se radi. Drugo je to sto se zadatak nalazi u odeljku stepenih redova jer se smenom svodi na to.

Moguce je da neki autor uvede svoje definicije. Jel to zbirka Merkle?

Autor knjige koju ja koristim je prof. sa FTN-a Mila Stojakovic.

Bas sam danas vezbao neke zadatke pa sam skontao da smenim sa t.
Nije mi jasno kako to nisam odmah skontao

Hvala, pozdrav!

Naziv poluprecnik konvergencije za kao i naziv krug konvergencije za skup . Mislim da nije lose reci red konvergira u svakoj tacki otvorenog kruga sa CENTROM u koordinatnom pocetku.