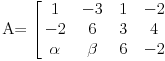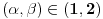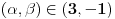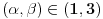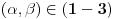[ emranonline @ 07.11.2008. 22:59 ] @
|
[ peddja_stankovic @ 08.11.2008. 07:25 ] @
Bice ti lakse ako prve dve kolone zamene mesta sa trecom i cetvrtom. To sme da se radi.
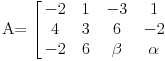 Prvu jednacinu pomnozi sa 2 saberi sa drugom i takodje prvu pomnozi sa -1 i saberi sa trecom dobijas matricu 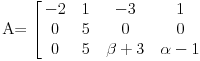 Sad drugu pomnozi sa -1 i saberi sa trecom dobije se 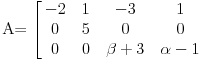 Dobili smo takozvanu trougaoni formu matrice. Kad je determinanta trougaona (ispog glavne dijagonale su sve nule), determinanta je jednaka proizvodu elemenata na glavnoj dijagolonali. Odavde se lako vidi sa je rang 2 ako je 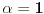 a a 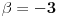 Zadnji red otpada pa je najveca poddeterminanta koja je razlicita od 0 reda 2 a to je rang matrice [Ovu poruku je menjao peddja_stankovic dana 08.11.2008. u 09:31 GMT+1] [ emranonline @ 08.11.2008. 09:03 ] @
Hvala
[ reni90 @ 22.10.2009. 16:01 ] @
da ne pravim novu temu
moze jedno pitanje kako da odredim rang prosirene matrice za matricu koja nije kvadratna rang matrice je dijagonalno od prvog clana a11 pa a22 pa a33 itd. ali kada imam transponovanu matricu gdje je broj kolona veci od vrsta npr 3x5 gdje je k kolona prosirena koju dijagonalu gledam tada? je li treba samo zadnji clan a33 zamjeniti sa a35 odnosno zadnjim clanom 5-te kolone? [ Nedeljko @ 22.10.2009. 18:27 ] @
Kakve sad dijagonale? Nisi dobro naučio rang.
[ reni90 @ 22.10.2009. 22:45 ] @
pa rang matrice dobijemo kad ispod glavne dijagonale svedemo sve elemente sa budu nule, onda je broj elemenata na dijagonali, koji su razliciti od nule. jednak rangu matrice
samo kada je treba od prosirene matrice odrediti ne znam po cemu gledam tu dijagonalu [ Nedeljko @ 23.10.2009. 07:21 ] @
Pa, i ovde možeš da koristiš glavnu dijagonalu, pa da čistiš matricu ispod nje ako ima više kolona, nego vrsta, ondnosno desno od nje ako ima više vrsta nego kolona.
[ reni90 @ 23.10.2009. 21:52 ] @
ne razumijes,
imam sistem linearnih jednadzbi i sada treba ga rijesiti Kroneker kapelijevim stavom za to trebam naci rang matrice A i rang transponovane Matrice A znam naci rang matrice A na osnovu prethodno sto sam napisao ali kako cu rang transponovane matrice ona ima jednu kolonu vise i ako je broj vrsta manji od kolona onda nijedan njen element ne lezi na toj glavnoj dijagonali ispadne prema tome da ne zavisi rang prosirene od te kolone ali zavisi eh sada treba nesto ili zmajeniti ili ne znam tacno sta uraditi da se nadje taj rang to pitam [ Nedeljko @ 23.10.2009. 23:13 ] @
Rang transponovane matrice matrice A je jednak rangu matrice A. No, tebi za Kroneker Kapelijevu teoremu ne treba rang transponovane matrice, već proširene matrice.
Koliki je rang matrice  ? ?Oduzimanjem druge vrste pomnožene sa 3 od treće vrste i zamenom mesta drugoj u četvrtoj koloni dobija se matrica  . .Dakle, rang je 2. Sa druge strane, matrica 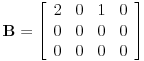 ima rang 1. Matrice A i B se razlikuju samo u poslednjoj koploni, a imaju različite rangove. Znači, rang zavisi od poslednej kolone. [ enter08 @ 24.10.2009. 16:00 ] @
Citat: Nedeljko: Rang transponovane matrice matrice A je jednak rangu matrice A. No, tebi za Kroneker Kapelijevu teoremu ne treba rang transponovane matrice, već proširene matrice. Koliki je rang matrice  ? ?Oduzimanjem druge vrste pomnožene sa 3 od treće vrste i zamenom mesta drugoj u četvrtoj koloni dobija se matrica  . .Dakle, rang je 2. Sa druge strane, matrica 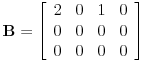 ima rang 1. Matrice A i B se razlikuju samo u poslednjoj koploni, a imaju različite rangove. Znači, rang zavisi od poslednej kolone. kako si dobio matricu B [iz A']? [ Nedeljko @ 24.10.2009. 17:02 ] @
Pa, nisam je dobio nikako, već sam konstruisao dve matrice, koje se razlikuju samo u poslednjoj koloni, da bih pokazao da rang zavisi i od te poslednje kolone. Konkretno, da bih otlonio ovu zabunu
Citat: reni90: ali kako cu rang transponovane matrice ona ima jednu kolonu vise i ako je broj vrsta manji od kolona onda nijedan njen element ne lezi na toj glavnoj dijagonali ispadne prema tome da ne zavisi rang prosirene od te kolone ali zavisi Naravno da zavisi. [ reni90 @ 24.10.2009. 20:51 ] @
ja se izvinjavam, napisao sam transponovane ali mislio samna prosirenu matricu
znaci kako odrediti rang prosirene matrice nadjemo sve nule ispod glavne dijagonale i na toj dijagonali vidimo rang glavne matrice i onda kako vidimo transponovane kada ona ima vise kolona, ne treba tu nista oduzimati ili slicno nego nekako se gleda ali ne znam kako [ Nedeljko @ 24.10.2009. 21:10 ] @
Elementarnim operacijama nad kolonama (i eventualno vrstama ako ti je lakše, ali nad kolonama obavezno) dovedi matricu na oblik, gde ispod glavne dijagonale imaš samo nule i gde nemaš nenula vrstu sa nulom na glavnoj dijagonali, prebroj nenula elemente na glavnoj dijagonali i to je to.
[ reni90 @ 24.10.2009. 21:59 ] @
ispod glavne dijagonele je uvijek nula
kada nadjem nule ispod glavn edijagonale i dodam samo jos jednu kolonu da bude prosirena opet je ispod glavne dijagonale nula prema tome znacilo bi da je rang prosirene uvijek jednag rangu obicne matrice ovi zaddaci sto su uradjeni nisu nista dodatno sabirali ili oduzimali kolone ili vrste samo su zakljucili sa matriice da je rang obicne npr 2 a prosirene 3 [ Nedeljko @ 24.10.2009. 22:14 ] @
[ Joxanaa @ 08.11.2009. 21:28 ] @
evo ja cu dati jedan primer matrice, a vi mi objasnite kakva je sad razlika izmedju obicne i prosirene matrice, tj. kako se odredjuje rang?
1 6 5 9 6 -1 3 3 -2 [ Nedeljko @ 09.11.2009. 06:57 ] @
Pa, ako je ovo proširena matrice sistema od 3 jedna;ine sa dve nepoynate, onda proširena matrica ima rang 3, a neproširena 2, pa taj sistem nije saglasan.
[ tamaraz92 @ 13.01.2010. 21:35 ] @
treba da resim sistem...pomocu kroneker kapelijeve teoreme da odredim kad je protivurecan, kad ima jedno res, a kad beskonacno mnogo, a onda pomocu kramera da nadjem ta resenja
alfa*x+y+z=1 x+alfa*y+z=1 x+y+alfa*z=1 dobila sam da je za alfa=1 rang matrice jednak rangu prosirene, rang je 1, znaci ima beskonacno mnogo res i za alfa<>1 rang matrice je 2 a rang prosine 3 znaci nema res... al ovako kad pogledam sistem vidi se da je za alfa=0 x=y=z=1/2 jel zna neko kako da rasim ovo? [ miki069 @ 13.01.2010. 23:50 ] @
Za alfa=1 je rang(A)=1 a rang(Ap)=1 i sistem ima beskonačno mnogo rešenja rešenje.
Za alfa=-2 je rang(A)=2 a rang(Ap)=3 i sistem nema rešenje. Za sve ostale alfe (raličite od 1 i od -2) je rang(A)=3 a rang(Ap)=3 i sistem ima jedinstveno rešenje. Ispravno je to što si primetila da za alfa=0 sistem ima jedinstveno rešenje. [ tamaraz92 @ 14.01.2010. 00:02 ] @
znaci rang matrice 3x3 moze da bude 3?? sad kapiram, hvala...
i imam jos jedan zad... :) x+y-z=1 2x-y-2z=3 4x+y+az=5 x+4y+z=b isto resiti sistem u zavisnosti od a i b, pomocu kronekera i kramera [ miki069 @ 14.01.2010. 00:31 ] @
Posle Gausovog metoda eliminacije sistem izgleda:
X + Y - Z = 1 -3*Y = 1 (a+4)*Z=0 2*Z=b za a<>-4 i b=0 je rang(A)=3 i rang(Ap)=3 i sistem ima jedinstveno rešenje X=4/3 , Y=-1/3, Z=0 za a<>-4 i b<>0 je rang(A)=3 i rang(Ap)=4 i sistem nema rešenje. za a=-4 (nezavisno od b) je rang(A)=3 i rang(Ap)=3 i sistem ima jedinstveno rešenje X=4/3 + b/2 , Y=-1/3, Z=b/2 Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|