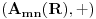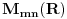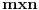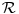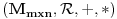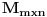[ Miladinovic @ 07.11.2008. 23:10 ] @
| Pozdrav, Trebam pokazati kojoj algebarskoj strukturi matrica Amn(R) pripada i to dokazati? Pošto da bi bila grupa mora da ima inverz, medjutim ako je determinanta matrice jednaka 0 onda naravno da matrica ne može imati inverz, a takodje ni operacija množenja nije komutivna ( sa izuzecima) da li to znači da je matrica u stvari monoid ili možda nije? |