[ Teoreticar @ 11.11.2008. 23:57 ] @
| Poznato je da ne postoji formula pomoću koje se mogu dobiti svi prosti brojevi... Ima li ovdje nekih pomaka ili pribliznih rjesenja... |
|
[ Teoreticar @ 11.11.2008. 23:57 ] @
[ Nedeljko @ 12.11.2008. 08:03 ] @
Postoji polinom stepena 25 sa 26 promenljivih i sa celim koeficijentima takav da je skup pozitivnihvrednosti tog polinoma za celobrojne vrednosti promenljivih jednak skupu prostih bojeva.
[ Teoreticar @ 12.11.2008. 10:39 ] @
Bio bi ti veoma zahvalan ako bi nam napisao taj polinom - ako si u mogućnosti, veoma me zanima.
Postojel jos neke pojedinosti u vezi toga... [ Nedeljko @ 12.11.2008. 10:55 ] @
Trenutno mi nije pri ruci knjiga "Hilbertovi problemi i logika" u kojoj je taj polinom napisan, ali cu se potruditi da ga okacim.
Ako ti ovo treba zbog kriptografije, onda ti je ovaj polinom lose resenje. [ Teoreticar @ 12.11.2008. 11:34 ] @
Ok, hvala ti mnogo...strasno bi me interesovao taj polinom.Ne treba mi za kriptografiju.
Na koji način bi se onda menjale vrednosti promenljivih u tom polinomu (cele vrednosti)? [ Nedeljko @ 12.11.2008. 17:56 ] @
Zameniš promenljive bilo kojim celim brojevima, izračunaš vrednost izraza, pa ako dobiješ pozitivnu vrednost, onda je to sigurno prost broj, a ako vrednost nije pozitivna, onda jednostavno nisi imao sreće - ne znaš ni da li je prost ni da li je složen. No, svaki prost broj se može dobiti kao pozitivna vrednost tog polinoma za neke celobrojne vrednosti promenljivih. Mislim da ću tek sutra moći da ti pošaljem polinom, ali samo da znaš da je mnogo "ružan".
[ Teoreticar @ 12.11.2008. 20:51 ] @
Ok, hvala ti mnogo,kad stignes napisi nam...
Pa cekaj, kada se taj polinom odredio...koje godine? Jer, zadnjih godina stalno se govori da ne postoji formula za dobijanje SVIH prostih brojeva. Prosvetlite me? [ Bojan Basic @ 12.11.2008. 22:20 ] @
Evo tog polinoma:
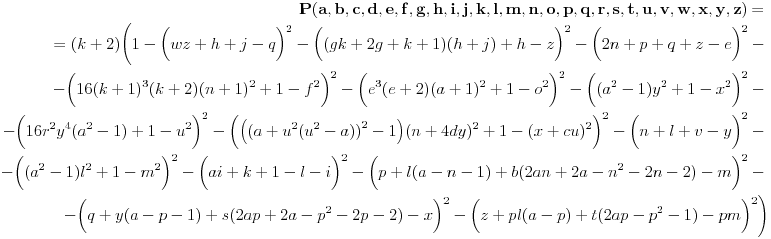 Moguće je poboljšati bilo stepen polinoma, bilo broj promenljivih. U prvom slučaju postoji polinom stepena  , ali on koristi , ali on koristi 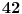 promenljive. Broj promenljivih je pak moguće svesti na promenljive. Broj promenljivih je pak moguće svesti na 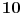 , no tada je stepen polinoma otprilike , no tada je stepen polinoma otprilike 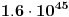 . .[Ovu poruku je menjao Bojan Basic dana 13.11.2008. u 13:49 GMT+1] [ miki069 @ 12.11.2008. 23:51 ] @
Ako ti nešta znači imam napisano programče u Delphi-ju koji za nekih 60 sekundi (na PIV računaru) izgeneriše prvih 4 000 000 prostih brojeva.
Statistika pojave je sledeća: - 1 000 prost broj je 7 919 (svaki osmi u proseku je prost), - 10 000 prost broj je 104 729 (svaki deseti u proseku), - 100 000 prost broj je 1 299 709 (svaki trinaesti u proseku), - 1000 000 prost broj je 15 485 709 (svaki petnaesti u proseku), - 4 000 000 prost broj je 67 667 969 (svaki sedamnaesti u proseku), - 10 000 000 prost broj je 179 424 691 (svaki osamnaesti u proseku). I tako sve su redji i redji... Al ih ima beskonačno mnogo... Vidi se da i tempo rasta koeficijenta razredjenosti polako pada... Da li taj koeficijent ima maximum (gornji limes konačan) kome polako teži? Ili i taj koeficijent teži beskonačnosti a njih opet ima beskonačno mnogo? Što je moguće ali je neinteresantno. Ili on već postoji a ja ga ne znam? Nemam programski odgovor jer ograničenje mi je LONGINT (mislim 2 na 64) u Delphi-ju. Ne mogu ga pustiti do beskonačnosti. Vreme nije problem.Ovaj skor je sa pisanjem rezultata u txt fajl. Moram onda malo da ga preradim. Ako ti nešta znači mogu ti dati to programče. [Ovu poruku je menjao miki069 dana 13.11.2008. u 02:15 GMT+1] [ Teoreticar @ 13.11.2008. 00:19 ] @
Hvala miki ,ali ne treba za sada...
Hvala Bojane... Ovo me malo zbunjuje ,jer polinom je faktorisan na dva izraza od kojih je jedan k+2 i ovaj u drugoj velikoj zagradi.Pa onda imamo UVEK proizvod dva cela broja ?? [ 987654321 @ 13.11.2008. 08:11 ] @
A da mozda tu ne koristi Rimanova zeta funkcija...
[ Nedeljko @ 13.11.2008. 11:04 ] @
Umesto
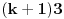 treba da stoji treba da stoji 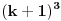 . .No, ako je polinom tacan i ovako faktorisan, to znaci da postoje dve vrednosti za  (0 i -2) za koje je vrednost polinoma pozitivna. (0 i -2) za koje je vrednost polinoma pozitivna.Postojanje ovakvog polinoma nije nikakva specificnost skupa prostih brojeva. Podkup skupa prirodnih brojeva se moze ovako predstaviti akko je rekurzivno nabrojiv. Primera radi, ovako se moze predstaviti skup svih prirodnih brojeva n, takvih da je zbir cifara broja nn!-n! deljiv sa n2+7. [ Nedeljko @ 13.11.2008. 11:06 ] @
miki069
O raspodeli niza prostih brojeva govori teorema o prostim brojevima (prime number theorem). [ Teoreticar @ 13.11.2008. 11:12 ] @
Ali za ako je k jednako -2 onda je vrijednost polinoma nula, jer je jedan faktor k+2
[ uranium @ 13.11.2008. 12:36 ] @
Citat: Teoreticar: Ovo me malo zbunjuje ,jer polinom je faktorisan na dva izraza od kojih je jedan k+2 i ovaj u drugoj velikoj zagradi.Pa onda imamo UVEK proizvod dva cela broja ?? Citat: Matijasevic's polynomial Notice that this polynomial factors! Look at the special form of the second part: it is one minus a sum of squares, so the only way for it to be positive is for each of the squared terms to be zero (this is a trick of Putnam's). ... bilo je već sličnih tema: http://www.elitesecurity.org/p810683 [ Bojan Basic @ 13.11.2008. 13:01 ] @
Citat: miki069: Vidi se da i tempo rasta koeficijenta razredjenosti polako pada... Da li taj koeficijent ima maximum (gornji limes konačan) kome polako teži? Ne znam šta podrazumevaš pod „tempom rasta koeficijenta razređenosti“, ali ovo u zagradi (svaki ... u proseku) asimptotski je 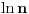 (dokazano), pa vidi da li to odgovara na tvoje pitanje. (dokazano), pa vidi da li to odgovara na tvoje pitanje.[ Nedeljko @ 13.11.2008. 13:46 ] @
Citat: Teoreticar: Ali za ako je k jednako -2 onda je vrijednost polinoma nula, jer je jedan faktor k+2 OK, 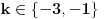 . Jeli sada bolje? . Jeli sada bolje?[ Nedeljko @ 13.11.2008. 13:49 ] @
Citat: uranium: Notice that this polynomial factors! Look at the special form of the second part: it is one minus a sum of squares, so the only way for it to be positive is for each of the squared terms to be zero (this is a trick of Putnam's). Stvarno, ako je poenta u tome da svi kvadrati budu nule, sta onda radi faktor k+2? [ Teoreticar @ 13.11.2008. 14:17 ] @
Da rezimiramo:
Skup pozitivnih vrednosti polinoma kojeg je napisao gosp. Bojan jednak je skupu prostih brojeva, polinom daje SVE proste brojeve za proizvoljne vrednosti promenljivih , gdje k može ima samo dve vrednosti i to:k=-1 v k=-3 Jeli sad sve OK? Evo još neki polinomi prvog stepena, nista posebno... [ Bojan Basic @ 13.11.2008. 14:30 ] @
Citat: Nedeljko: Stvarno, ako je poenta u tome da svi kvadrati budu nule, sta onda radi faktor k+2? Faktor 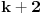 je upravo prost broj koji dobiješ kao rezultat polinoma kada promenljivima dodeliš vrednosti. Dakle, prost broj je upravo prost broj koji dobiješ kao rezultat polinoma kada promenljivima dodeliš vrednosti. Dakle, prost broj 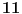 dobićeš za dobićeš za 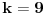 (i pogodne vrednosti ostalih slova), dok nema načina da vrednost polinoma bude pozitivna za npr. (i pogodne vrednosti ostalih slova), dok nema načina da vrednost polinoma bude pozitivna za npr. 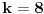 . .Citat: Ne (vidi prethodni pasus). [ uranium @ 13.11.2008. 14:36 ] @
@Nedeljko:
pogledaj screenshot u prilogu ( kako glasi formulacija teoreme ... ) [ Teoreticar @ 13.11.2008. 15:04 ] @
Ok, hvala ti Bojane, mislim da je sad OK.
Znaci ako zelim da proverim recimo da li je 83 prost ili slozen uzimam k=81. Dalje, trazim vrednosti ostalih promenjivih za koje su svi kvadrati u drugom faktoru nula sto ce rezultirati da drugi faktor ima vrednost 1. Ako je to moguce (da je vrednost drugog faktora 1) broj jeste prost ?? [ Nedeljko @ 13.11.2008. 16:07 ] @
Sad je sve jasno. Pored ostalog i to da ovaj polinom nema nikakvu prakticnu primenu.
[ Teoreticar @ 13.11.2008. 16:21 ] @
Zar ne mozemo primeniti na ispitivanje da li je neki broj prost?
Ali, ako mogu dobro videti bilo bi jako tesko ?? [ Nedeljko @ 14.11.2008. 07:33 ] @
Za to se koriste drugi algoritmi. Pre svega, testovi pseudoprimalnosti, a ako bas hoces da budes siguran da je neki broj prost, onda su neki indijci pronasli algoritam polinomijalne slozenosti za testiranje primalnosti. No, i taj algoritam je isuvise skup za prakticnu primenu, pa se pribegava (aproksimativnim) testovima (pseudo)primalnosti.
[ miki069 @ 16.11.2008. 07:08 ] @
Uklapa se ln(n) u koeficijent razudjenosti.
Sto je n veci i veci sve je blizi iznosu ln(n). Pustao sam program do milijardu prostih brojeva. Zato kasnim. Hvala Bojane. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|