jel moze tacno tekst zadatka?

Baš tako kao što sam napisao. Zadatak je uzet iz zbirke zadataka Linearna Algebra od Stojana Radenovića, primer 4.21, pod a).

imam tu zbirku i vidim resenje ali bi ja isto to dobio seljacki (a tako je i on posle odradio). Znaci, iz aviona se vidi da su a1 i a3 linearno zavisni a da je a2 nezavisan od njih. Znaci a1 i a2 bi cinili bazu ili a2 i a3. to su ta dva resenja. To sam i ranije znao. Iako postujem Radenovica, malo je zadatak konfuzno postavljen za moj ukus. Covek je predavao predmet pa valjda zna bolje od mene.

A je l' mogu da nađem baze preko dimenzije? Nađem dimenziju i toliko vektora mora biti u bazi. I onda vidim koji su linearno nezavisno, oni ne mogu da čine bazu. Svi ostali da. I to je to? Je l' bi ovo važilo za sve slučaje kada se traže baze?

Linearno nezavisni vektori čine bazu linearnog prostora, samo trebaš proveriti linernu nezavisnost data 3 vektora, mada ovde je očito koji su zavisni prvi i treći, jer je ovaj 3x prvi, ali kod složenijih primera se to pak i ne može lako videti.

1. način, tj. postpupak da pokažeš da su vekotri nezavisni je preko matrice

.

elementarnim operacijama svedeš na

.

I vidiš da je rang=2, pa imaš 2 nezavisna vektora i jedan zavisan od prvog kako je @peddja_stankovic napomenuo.

2. način jeste da predstaviš njihove linearne kombinacije




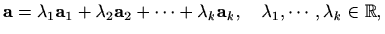
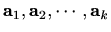
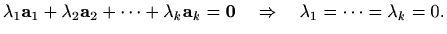
Pa su vektori linearno nezavisni ako odnosno njihov zvir jednak nuli.

Ako imas vektore iz R4 ne moras posmatrati prostor R4 da bi prema tome imao 4 bazna vektora. Moze biti rec o podprostoru tog prostora koji moze biti i dimenzije koja je manja od 4. Na primer skup vektora (x,y,z,0) cine vektorski podprostor koji je dimenzije 3 ( ima 3 vektora u bazi).

Medjutim sta je mene zbunjivalo. Ovde pise sve baze sistema vektora a1, a2 i a3. Ovde mi nedostaje o kom podprostoru je rec, pa bi baza mogla biti i neki drugi vektori preko kojih se mogu izraziti a1,a2 i a3. Eto i dalje tvrdim da je zadatak konfuzno postavljen.