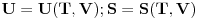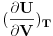[ petarm @ 21.11.2008. 23:19 ] @
|
[ Mlatko @ 22.11.2008. 03:24 ] @
Pozdrav momce.
Ako sam dobro shvatio, trazis objasnjenje zasto su U i S funkcije (samo) T i V? Pojednostavljeno, moze se reci ovako: U, tj unutrasnja energija je odredjena pritiskom, volumenom i temperaturom, dakle U=U(p,T,V). No posto su p,V i T povezani jednadzbom stanja p=p(V,T), to znaci da je U=U(p(V,T),T,V)=U(T,V), tj U je funkcija varijabli T i V. Za S vrijedi slicno, pogledas definiciju za S, npr u ravnoteznom stanju je dS=d'Q/T. Dakle, S je funkcija od T i svega onoga o cemu je ovisna funkcija Q. Kako prema 1. zakonu vrijedi d'Q = dU + pdV, to znaci da je Q ovisno o U, p i V. Posto je U ovisno o T i V (vidi gore), zatim p takodjer ovisno o T i V (vidi gore), jasno je da je Q zapravo na koncu ovisno o T i V. Iz svega recenog slijedi da je S funkcija od T i V tj S = S(T,V). Je li to bilo ono sto si htio pitati, ili sam pogresno razumio? Nego, ne mogu da ne pitam, sta ti znaci ono "ok" u nazivu teme? :) [ petarm @ 22.11.2008. 18:49 ] @
Citat: Zeza me "o" na tastaturi pa ga iz tog razloga nema uvek! Pre svega hvala ti na odgovoru! Citat: Mlatko: Pozdrav momce. Ako sam dobro shvatio, trazis objasnjenje zasto su U i S funkcije (samo) T i V? Zasto uzimam da su fje samo T i V Citat: Mlatko: Pojednostavljeno, moze se reci ovako: U, tj unutrasnja energija je odredjena pritiskom, volumenom i temperaturom, dakle U=U(p,T,V). No posto su p,V i T povezani jednadzbom stanja p=p(V,T), to znaci da je U=U(p(V,T),T,V)=U(T,V), tj U je funkcija varijabli T i V. Za S vrijedi slicno, pogledas definiciju za S, npr u ravnoteznom stanju je dS=d'Q/T. Dakle, S je funkcija od T i svega onoga o cemu je ovisna funkcija Q. Kako prema 1. zakonu vrijedi d'Q = dU + pdV, to znaci da je Q ovisno o U, p i V. Posto je U ovisno o T i V (vidi gore), zatim p takodjer ovisno o T i V (vidi gore), jasno je da je Q zapravo na koncu ovisno o T i V. Iz svega recenog slijedi da je S funkcija od T i V tj S = S(T,V). Je li to bilo ono sto si htio pitati, ili sam pogresno razumio? Hvala! Znas sta mene ustvari buni. Za 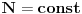 koristi se Bornov cetvorougao koristi se Bornov cetvorougaoV F T U 0 G S H P Gde mi 0 predstavlja dve ukrstene "strele" Ovaj cetvorougao je jako koristan za nalazenje prvih parcijalnih izvoda, a uzima se iz njega npr. U=U(S,V). Odnosno nije nuzno uzimati U=U(T,V) [ Mlatko @ 23.11.2008. 19:43 ] @
Citat: petarm: uzima se iz njega npr. U=U(S,V). Odnosno nije nuzno uzimati U=U(T,V) Hint: slozene funkcije. Nije nuzno uzimati U=U(T,V) jer od varijabli T i V uvijek mozes definirati neke "korisne" funkcije (npr S=S(T,V) ), prepoznati ih u definiciji funkcije U, i onda U postaje "slozena funkcija" U=U(S,V) ili U=U(S,T) ili U=U(S), ovisno kako je definirana funkcija S. (npr u funkciji U = 2T + V + V^2, gdje je U=U(T,V), mozemo definirati S = 2T+V, pa U postaje slozena funkcija s varijablama S i V, tj U=U(S,V) ) Zasto nam treba definiranje dodatnih funkcija, poput pomenute S? Zato sto promatranjem ovako definiranog S, i parcijalnih derivacija od U po S, mozemo dobiti neke nove informacije o fizikalnim procesima ili barem pojednostavljenje nekih vec dobijenih. Osim toga tako definirana funkcija S ne mora biti neka apstraktna funkcija koja bi nam eto samo pomagala kod interpretacije fizikalnih procesa, nego je cesto i konkretna mjerljiva fizikalna velicina. Zato se i definiraju termodinamicki potencijali, jer npr promatranjem njih kao funkcija, te njihovih parcijalnih derivacija, dobijamo neke informacije o termodinamickim procesima (na primjer kod procesa u kojima je p=const i S = const, definiranje funkcije H i njeno promatranje nam pomaze jer je karakteristika takvih procesa da sustav tezi stanju minimalne entalpije H), a mogu posluziti i za racunanje V,T,P i S, (u cemu pomaze Bornov cetverokut). [ petarm @ 25.11.2008. 08:36 ] @
Citat: Mlatko: Hint: slozene funkcije. Nije nuzno uzimati U=U(T,V) jer od varijabli T i V uvijek mozes definirati neke "korisne" funkcije (npr S=S(T,V) ), prepoznati ih u definiciji funkcije U, i onda U postaje "slozena funkcija" U=U(S,V) ili U=U(S,T) ili U=U(S), ovisno kako je definirana funkcija S. (npr u funkciji U = 2T + V + V^2, gdje je U=U(T,V), mozemo definirati S = 2T+V, pa U postaje slozena funkcija s varijablama S i V, tj U=U(S,V) ) Zasto nam treba definiranje dodatnih funkcija, poput pomenute S? Zato sto promatranjem ovako definiranog S, i parcijalnih derivacija od U po S, mozemo dobiti neke nove informacije o fizikalnim procesima ili barem pojednostavljenje nekih vec dobijenih. Osim toga tako definirana funkcija S ne mora biti neka apstraktna funkcija koja bi nam eto samo pomagala kod interpretacije fizikalnih procesa, nego je cesto i konkretna mjerljiva fizikalna velicina. Zato se i definiraju termodinamicki potencijali, jer npr promatranjem njih kao funkcija, te njihovih parcijalnih derivacija, dobijamo neke informacije o termodinamickim procesima (na primjer kod procesa u kojima je p=const i S = const, definiranje funkcije H i njeno promatranje nam pomaze jer je karakteristika takvih procesa da sustav tezi stanju minimalne entalpije H), a mogu posluziti i za racunanje V,T,P i S, (u cemu pomaze Bornov cetverokut). Hvala na odgovoru pre svega! Ovde to nije problem! Ali mogu dobiti da dokazem neki slozeniji izraz u kojem ce  , ,  , npr. , npr.  figurisati i da bude prilicno tesko utvrditi od cega poci; od kojih zavisnosti. Zato sam mislio da ovde okacim ne bi li mi neko preneo svoja iskustva il mozda koji trik ovde napisao sto bi mi znacilo za dalje. Naravno to ostaje i za ubuduce. Cini mi se da je dosta veliki problem u ovoj da kazem statistickoj termodinamici sto covek moze da se vrti kroz neke jednacine da dobija brojne relacije, ali ne i ono sto mu treba. Pak ako brzo otkrije sta treba da iskoristi odakle da krene zadatak se veoma brzo resava! Naravno ne bi bilo lose ni ako neko moze da preporuci neku zbirku gde je ova oblast dobro odradjena. figurisati i da bude prilicno tesko utvrditi od cega poci; od kojih zavisnosti. Zato sam mislio da ovde okacim ne bi li mi neko preneo svoja iskustva il mozda koji trik ovde napisao sto bi mi znacilo za dalje. Naravno to ostaje i za ubuduce. Cini mi se da je dosta veliki problem u ovoj da kazem statistickoj termodinamici sto covek moze da se vrti kroz neke jednacine da dobija brojne relacije, ali ne i ono sto mu treba. Pak ako brzo otkrije sta treba da iskoristi odakle da krene zadatak se veoma brzo resava! Naravno ne bi bilo lose ni ako neko moze da preporuci neku zbirku gde je ova oblast dobro odradjena.[ petarm @ 02.12.2008. 20:40 ] @
Ja mislim da bi se gornji zadatak trebao ovako resavati:
ZAD Polazeci od 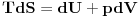 pokazati da vazi pokazati da vazi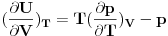 RES: Polazeci od II principa termodinamike imamo 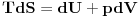 podelimo levu i desnu stranu jednacine sa  i dobijamo i dobijamo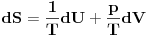 Iz 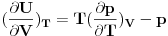 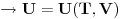 Pa je 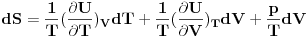 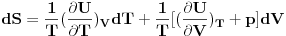 Kako je 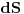 totalni diferencijal onda je totalni diferencijal onda je 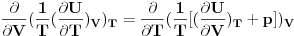 Pa je 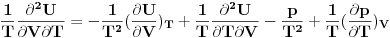 Iz pretpostavke da radimo u jednoj fazi imamo da su parcijalni izvodi neprekidni pa se dva clana potiru i ostaje 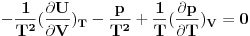 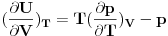 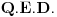 Ovim sam inace pokazao da iz izbora 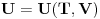 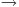 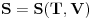 na osnovu II principa termodinamike te mislim da je ovo moje resenje iz tog razloga bolje nego da se odmah pretpostavi zavisnost entropije. Inace zadatak je iz zbirke Kubo. na osnovu II principa termodinamike te mislim da je ovo moje resenje iz tog razloga bolje nego da se odmah pretpostavi zavisnost entropije. Inace zadatak je iz zbirke Kubo. I ja sam naglasio sa se sve izvodi u jednoj fazi jer na nekom od faznih prelaza nemamo neprekidnost parcijalnih izvoda sto iz nekih razloga autori uvek podrazumevaju, a ne naglasavaju. U okviru jedne faze nema problema. [ petarm @ 05.12.2008. 20:25 ] @
Jel se slazete s ovim? Da je ovako najtacnije resiti!
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|