[ petarm @ 06.12.2008. 15:04 ] @
|
[ zozox @ 14.12.2008. 17:35 ] @
pa mozda je neka instrumetalna karakteristika
[ zozox @ 14.12.2008. 18:28 ] @
imam knjigu na pdf formatu Fundamentals of Powder Diffraction and Structural Characterization of Materials, Vitalij K. Pecharsky i Peter Y. Zavalij, pa ako te interesuje javi da ti posaljem knjigu na mail
[ zozox @ 14.12.2008. 18:31 ] @
imam knjigu na pdf formatu Fundamentals of Powder Diffraction and Structural Characterization of Materials, Vitalij K. Pecharsky i Peter Y. Zavalij, pa ako te interesuje javi da ti posaljem knjigu na mail
[ petarm @ 20.12.2008. 13:35 ] @
Posalji ako ti nije problem! Unapred hvala
[ tihana_m @ 28.12.2008. 17:47 ] @
A je apsorpcioni faktor. Bez obzira koja se metoda koristi, kristal delimicno apsorbuje i upadni i difraktovani snop zbog cega dolazi do smanjenja intenziteta.
POLARIZACIONI FAKTOR (p)-u opstem slucaju rengensko zracenje je nepolarizovno.Elektricni vektor je moguce predstaviti kao zbir dva vektora , od kojih jedan normalan na ozracenu povrsinu, a drugi paralelan njoj. Svaki od tih vektora ima amplitudu √2/2. Neka primarno, nepolarizovno zracenje pada pod uglom θ na kristal. Pri rasipanju rengenskih zraka na elektonima dolazi do promene ukupne amplitude elekticnog vektora, koja zavisi od elekronske gusine u posmatranoj ravini . Eletroni nisu podjednako efikasni pri raspanju paralelne i normalne komponente elekricnog vektora. Zbog toga je i difraktovano zracenje delimicno polarizovano. Amplituda noramlne komponente eletricnog vektora izracunava se iz izraza √2/2cos2θ. Ukupni intezitet elekricnog vektora proporcionalan je zbiru kvadrata amplituda paralelne i noramlne kompontente. Pa je polarizacioni faktor p=(1+cos2θ)/2. ( kosinus na kvadrat:-)). I ovaj fakor je jednak za sve kristalografske metode osim kad se koristi vec polarizovan primarni snop, u tom slucaju je p=(1+Kcos2θ)/1+K ( i ovde je kosinus na kvadrat samo nisam uspela to da napisem) gde je K=cos2θm ( takode je kosinus na kvadrat, a m je ovde index-u) θm je Bragov ugao difrakcije kristala monohomatora. LORENCOV FAKTOR (L)-matematicki oblik zavisi od primenjene metode. Konkretno, na Lorencov faktor sprasenog uzorka utice vise cinilaca. 1. kada ravini reflektovanja zaklapaju ugao θ sa upadnim snopom, Bragov zakon je zadovoljen i dolazi do difrakcije maksimalnog intenziteta. Medutim, jedan deo energije bice difraktovan u skoro istom pravcu cak i ako se ravni malo pomere od tacnog Bragovog ugla. Vrednost intenziteta zavisi od ugaonog intervala ±δθ u kome kristal rotira, a u kome je energija difraktovanog snopa zracenja. Intezitet difrakovanog snopa za jedan prolazak kristala kroz polazaj reflektovnja, odnosno kroz ugaoni interval ±δθ, proporcionalan je 1/sinθ. Drugim recima, intezitet ce biti veci na malim uglovima θ, a manji na velikim uglovima. 2. sirina difrakcione linije ima upravo suprotan efekat dat izrazom 1/cosθ 3. broj kristala orijentisanih tako da zaklapaju Bragov ugao ili su blizu tog ugla. broj ovako orijentisanih kristala proporcionalan je cosθ i vrlo je mali na velikim Bragovim uglovima 4. refleksije ciji je ugao 2θ oko 90 stepeni daju na Debaj-Sererovom filmu slabiji integrisani intenzitet po jedinicnoj duzini difrakcione linije nego refleksije na vecim ili manjim uglovima. Posto je duzina difrakcione linije 2πrsin2θ, gde je r poluprecnik komore, onada je relativni intezitet po jedinicnoj duzini linije proprcionalan izrazu 1/sin2θ.Ovaj faktor ponekad se naziva i geomerijski faktor. Kombinacija ovih cinilaca dobija se Lorencov faktor za Debaj-Sererovu metodu i difrakometriju praha Lorencov i polarizaciono faktor obicno se kombinuju u zajedniciki Lorenc-polarizacioni ili Lp faktor. [ petarm @ 01.01.2009. 20:28 ] @
Citat: tihana_m: A je apsorpcioni faktor. Bez obzira koja se metoda koristi, kristal delimicno apsorbuje i upadni i difraktovani snop zbog cega dolazi do smanjenja intenziteta. Kako se odredjuje apsrpcioni faktor  . Iz tablica? . Iz tablica?Citat: tihana_m: POLARIZACIONI FAKTOR (p)-u opstem slucaju rengensko zracenje je nepolarizovno.Elektricni vektor je moguce predstaviti kao zbir dva vektora , od kojih jedan normalan na ozracenu povrsinu, a drugi paralelan njoj. Svaki od tih vektora ima amplitudu √2/2. Neka primarno, nepolarizovno zracenje pada pod uglom θ na kristal. Pri rasipanju rengenskih zraka na elektonima dolazi do promene ukupne amplitude elekticnog vektora, koja zavisi od elekronske gusine u posmatranoj ravini . Eletroni nisu podjednako efikasni pri raspanju paralelne i normalne komponente elekricnog vektora. Zbog toga je i difraktovano zracenje delimicno polarizovano. Amplituda noramlne komponente eletricnog vektora izracunava se iz izraza √2/2cos2θ. Ukupni intezitet elekricnog vektora proporcionalan je zbiru kvadrata amplituda paralelne i noramlne kompontente. Pa je polarizacioni faktor p=(1+cos2θ)/2. ( kosinus na kvadrat:-)). I ovaj fakor je jednak za sve kristalografske metode osim kad se koristi vec polarizovan primarni snop, u tom slucaju je p=(1+Kcos2θ)/1+K ( i ovde je kosinus na kvadrat samo nisam uspela to da napisem) gde je K=cos2θm ( takode je kosinus na kvadrat, a m je ovde index-u) θm je Bragov ugao difrakcije kristala monohomatora. Evo da se lakse cita :) 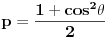 - kad je primarni snop nepolarizovan - kad je primarni snop nepolarizovan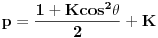 - kad je primarni snop polarizovan - kad je primarni snop polarizovanCitat: tihana_m: LORENCOV FAKTOR (L)-matematicki oblik zavisi od primenjene metode. Konkretno, na Lorencov faktor sprasenog uzorka utice vise cinilaca. 1. kada ravini reflektovanja zaklapaju ugao θ sa upadnim snopom, Bragov zakon je zadovoljen i dolazi do difrakcije maksimalnog intenziteta. Medutim, jedan deo energije bice difraktovan u skoro istom pravcu cak i ako se ravni malo pomere od tacnog Bragovog ugla. Vrednost intenziteta zavisi od ugaonog intervala ±δθ u kome kristal rotira, a u kome je energija difraktovanog snopa zracenja. Intezitet difrakovanog snopa za jedan prolazak kristala kroz polazaj reflektovnja, odnosno kroz ugaoni interval ±δθ, proporcionalan je 1/sinθ. Drugim recima, intezitet ce biti veci na malim uglovima θ, a manji na velikim uglovima. 2. sirina difrakcione linije ima upravo suprotan efekat dat izrazom 1/cosθ 3. broj kristala orijentisanih tako da zaklapaju Bragov ugao ili su blizu tog ugla. broj ovako orijentisanih kristala proporcionalan je cosθ i vrlo je mali na velikim Bragovim uglovima 4. refleksije ciji je ugao 2θ oko 90 stepeni daju na Debaj-Sererovom filmu slabiji integrisani intenzitet po jedinicnoj duzini difrakcione linije nego refleksije na vecim ili manjim uglovima. Posto je duzina difrakcione linije 2πrsin2θ, gde je r poluprecnik komore, onada je relativni intezitet po jedinicnoj duzini linije proprcionalan izrazu 1/sin2θ.Ovaj faktor ponekad se naziva i geomerijski faktor. Kombinacija ovih cinilaca dobija se Lorencov faktor za Debaj-Sererovu metodu i difrakometriju praha Lorencov i polarizaciono faktor obicno se kombinuju u zajedniciki Lorenc-polarizacioni ili Lp faktor. Cini mi se da je i za ovo iracunavanje ipak potrebno koristiti neke tablice? Citat: petarm: Intenzitet neke linije kod vezbe difrakcija na kristalnom prahu racuna se kao 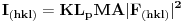 gde je  - koef. skale; - koef. skale; 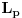 - Lorenc polarizacioni faktor; - Lorenc polarizacioni faktor;  - faktor multipliciteta; - faktor multipliciteta; 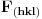 - strukturni faktor - strukturni faktorOd cela zavisi 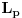 i sta je i sta je  ? ?Znas li mozda nesto vise reci o ostalim faktorima koji se pojavljuju u jednakosti. Po meni bi ovo  trebalo da sluzi za neka visestruka merenja, a trebalo da sluzi za neka visestruka merenja, a  pp da je korekcija na pojavu vise razlicitih refleksa sa iste pljosni. Hvala ti na odgovoru! pp da je korekcija na pojavu vise razlicitih refleksa sa iste pljosni. Hvala ti na odgovoru! [ tihana_m @ 04.01.2009. 12:32 ] @
1. Greska oko polarizacionog faktora ( zato sto me znam ovde kako bih to napisala, a kad napisem u Word-u ne mogu da prebacim) pa ti saljem na mail.
2. Apsorpcioni faktor- ako rengenski snop ima intenzitet I, pri prolasku kroz kristal debljine dx dolazi do promene intenziteta dI tj, dI/I=-μdx, μ-linearni koeficijent apsorpcije i negova vrednos zavisi od hemijskog sastava uzorka (tezi elementi imaju vece vrednosti) i od talasne duzine rengenskog zracenja. Za razlicite metode i razlicite vrste uzoraka A se izracunava na razlicite nacine. Moze i da se zanemari kada je μ malo. 3. M fakor multipliciteta ima ulogu samo pri radu sa sprasenim uzorcima. Moze se definisati kao broj nizova ravni istog medupljosnog rastojanja. 4.K je fakor skale 5. F (hkl) strukturni faktor-ima malo vecu filozofiju. I brdo formula. ako bude trebalo javi A sve to o cemu opisem imas u knjizi Liljana Karanovic, Dejan Poleti RENGENSKA STRUKTRNA ANALIZA POZDRAV Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|