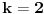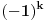[ viktor1986 @ 18.12.2008. 12:01 ] @
|
| Poz
Imam problem tj. ne poklapa mi se rezultat tacno sa resenjem iz knjige.Naime,imam integral
I=(2/pi) * integral ((x^2)*cos kx dx) a integral ide od 0 do pi
Dobio sam resenje (-4) / (k^2). E sada imam problem jer mi je u resenju napisano (-1)^k * (4/k^2). Sta je pravilno da se pise, tj. zasto se uvodi ono (-1)^k ??? Zbog toga sto se sa time simbolise red ili sta...?
Ovo mi treba za seminarski rad iz matematike pa zato pitam.
Unapred zahvalan na pomoci.
|
[ Bojan Basic @ 18.12.2008. 12:20 ] @
Citat:
viktor1986:
Sta je pravilno da se pise, tj. zasto se uvodi ono (-1)^k ??? Zbog toga sto se sa time simbolise red ili sta...?
Problem je u tome što se tvoj rezultat i rezultat iz rešenja razlikuju (npr. za
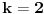
tvoj rezultat je

, a u rešenju je

). Dakle, ono
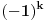
nije stvar stila, već je suštinski bitno.
[ viktor1986 @ 18.12.2008. 13:01 ] @
Citat:
Bojan Basic: Problem je u tome što se tvoj rezultat i rezultat iz rešenja razlikuju (npr. za
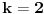
tvoj rezultat je

, a u rešenju je

). Dakle, ono
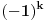
nije stvar stila, već je suštinski bitno.
Aj mozda sam nesto predvideo ali zadatak glasi da funkciju f(x)=x^2 razvijem u furijeov red na odsecku -pi, pi
Evo kako je to u knizi...
[ viktor1986 @ 18.12.2008. 13:38 ] @
Je li, da nije fazon u tome da je rezultat u zavisnosti od odsecka,tj. rezultat je -4/k^2 od 0 do pi a da je
(-1)^k * (4/k^2) na odsecku -pi do pi? Molim pomoc...
[ marko1981 @ 18.12.2008. 13:53 ] @
(-1)^k se cesto pojavljuje u Fuorier-ovim redovima i posledica je jednakosti
cos(k*pi) = (-1)^k
koja treba da ti se pojavi prilikom racunanja intergrala u koeficijentima.
(Slicno bude i za sinus)...
[ viktor1986 @ 18.12.2008. 18:41 ] @
OK hvala
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.