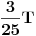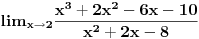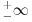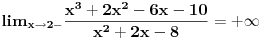Ako sam dobro shvatio, treba ti ostatak pri celobrojnom deljenju S sa T.


Ako je

S/T = 64.12 (ovo je "pravo" deljenje, ne celobrojno)

onda je

S = 64 * T + 0.12 * T

odnosno

S = 64 * T + R, gde je R ostatak

znaci, ostatak je

R = S - 64 * T

odnosno

R = 0.12 * T


Nadam se da sam dobro razumeo sta si pitao.

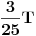
Tj. ostatak je , što znači da je neophodno da T bude deljiv sa 25. (Inače, s postavkom takva kakva je, bolji odgovor od ovoga ne može se dati.)

Ja bih ovo pokusao da resim nagadjanjem, ali cini mi se da ima vise mogucih resenja(?).
Ne mora ići nagađanjem, ali rješenja za ovaj slučaj ima beskonačno.
Najmanji par je S=1603 i T=25 zbog R=0.12*.(100R=12 ili 25R=3)
1603/25=64+3/25

Treba da resim limes:

Lim x^3+2x^2-6x-10/x^2+2x-8
x-->2

kada uprostim imenilac dobijem (x+4)(x-2) sada po metodi resavanja tog limesa treba da podelim brojilac sa (x+4) da bi se posle to skratilo, kad to delim ostane mi ostatak -18. Sta s tim da radim.

Ako ti je ovo razlomak :(x^3+2x^2-6x-10)/(x^2+2x-8) ubaci da je x=2
da vidiš kojeg je oblika limes.Ispade (8+8-12-10)/(4+4-8)=(-6)/0, a to ti je
- beskonačno.Moguće da si pogrešno ukucao zadatak, pa ako je i brojnik
nula, onda ne treba dijeliti sa (x+4) već sa (x-2) kako bi kraćenjem izbacio
ovaj neugodni faktor koji teži nuli.

Ako sam te dobro razumeo zadatak glasi:


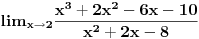
Pa trebalo bi da tezi :

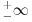
Kada se priblizavas dvojci sa "leve strane" ,neka je to broj 1.99999 ili 1.9999999999


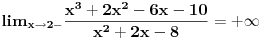
A ako se priblizavas sa "desne strane", npr 2.000001 ili 2.0000000001



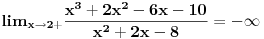
Ja se nadam da sam dobro izracunao.

Da, to je ispravno resenje. Evo jos malo detalja.

Ako "zamenis" 2 u ceo razlomak, dobices -6/0, znaci po apsolutnoj vrednosti resenje je beskonacnost.

Sto se tice znaka beskonacnosti, ona zavisi od toga da li x->2+ ili x->2- kao sto je RMAN rekao.

U imeniocu imas parabolu okrenutu na gore koja sece x-osu u -4 i u 2.

1. x->2+ (x=2.000000000000....0001)

- Na grafiku ces lako videti da je vrednost parabole iznad x-ose, pa je imenilac 0+, tj. 0.0000000...0001, odnosno, beskonacno mali POZITIVAN broj.

- Dakle, resenje je -6 / (0+) = -beskonacno (jer delimo negativan broj pozitivnim)

2. x->2- (x=1.9999999999999...9999)

- Na grafiku ces lako videti da je vrednost parabole ispod x-ose, pa je imenilac 0-, tj. -0.0000000...0001, odnosno, beskonacno mali NEGATIVAN broj.

- znaci resenje je -6 / (0-) = +beskonacno (jer delimo negativan broj negativnim).

Zadatak sam dobio za vezbu i nemam resenje. Ako delim polinom u brojiocu sa (x-2) kao sto je zzzz napisao dobijem opet ostatak -14.
Moguce da nisam prepisao sa table dobro ali sam siguran da zadatak nema formu da limes tezi 2+ ili 2- jer takve zadatke ne dobijamo. Jos cu proveriti ispravnost zadatka, u svako slucaju hvala Vam puno za pomoc.

Eh da, tek kada sam provezbao asimptote i prilazenje tackama sa leve i desne strane shvatih da ste mi resili zadatak. Hvala jos jednom.