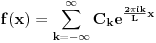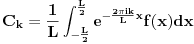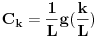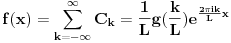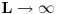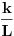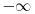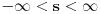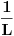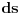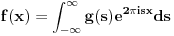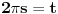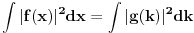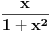[ petarm @ 05.01.2009. 14:43 ] @
|
[ Nedeljko @ 06.01.2009. 13:11 ] @
Vidi u udžbeniku analize II od Adnađevića i Kadelburga tačku "Furijeov integral" na kraju knjige. Imaš put do integrala preko reda.
[ petarm @ 17.01.2009. 10:25 ] @
Pogledao sam knjigu i evo kacim moj odgovor uz ovaj post!
[ petarm @ 27.01.2009. 12:15 ] @
Ima li odgovora na ovo?
[ Nedeljko @ 28.01.2009. 11:05 ] @
Koliko se secam, furijeova transformacija je operator definisan na prostoru integrabilnih funkcija, dakle
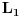 . Tada Furijeova transformacija funkcije postoji. Integrabilnost funkcije . Tada Furijeova transformacija funkcije postoji. Integrabilnost funkcije  znaci da je ta funkcija merljiva po Lebegu i da je znaci da je ta funkcija merljiva po Lebegu i da je 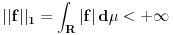 , tako da je po osnovnoj integralnoj nejednakosti , tako da je po osnovnoj integralnoj nejednakosti 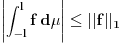 , odakle je , odakle je 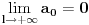 . Ako pak funkcija pruipada prostoru . Ako pak funkcija pruipada prostoru  , onda vaze Parsevalova jednakost i formula inverzije. Ne secam se bas svega najbolje. U svakom slucaju, te teoreme mozes naci u knjizi "Real and Complex Analyzis" autora Waltera Rudina. , onda vaze Parsevalova jednakost i formula inverzije. Ne secam se bas svega najbolje. U svakom slucaju, te teoreme mozes naci u knjizi "Real and Complex Analyzis" autora Waltera Rudina.[ petarm @ 29.01.2009. 12:19 ] @
[ Nedeljko @ 29.01.2009. 13:54 ] @
Svakom vektoru
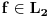 moze se pridruziti ograniceni linearni funkcional moze se pridruziti ograniceni linearni funkcional 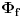 prostora prostora 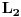 , (tj. vektor , (tj. vektor 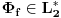 ) definisan na sledeci nacin: ) definisan na sledeci nacin: 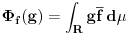 , pri cemu je samo preslikavanje , pri cemu je samo preslikavanje 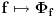 antilinearno i svakom vektoru pridruzuje vektor iste norme. Takodje, Pomenuto preslikavanje je bijektivno, pa je otuda antilinearno i svakom vektoru pridruzuje vektor iste norme. Takodje, Pomenuto preslikavanje je bijektivno, pa je otuda 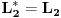 . No, ne vidim kakve veze to ima sa Parsevalovom jednakoscu. . No, ne vidim kakve veze to ima sa Parsevalovom jednakoscu.Da bi Furijeova transformacija funkcije  uopste postojala, treba da bude uopste postojala, treba da bude 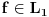 , tako da Parsevalova jednakost i formula inverzije zahtevaju da bude , tako da Parsevalova jednakost i formula inverzije zahtevaju da bude 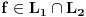 ali pogledacu u Rudinu, pa cu ti reci sve tacno. ali pogledacu u Rudinu, pa cu ti reci sve tacno.[ petarm @ 30.01.2009. 20:26 ] @
Citat: Nedeljko: Svakom vektoru 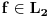 moze se pridruziti ograniceni linearni funkcional moze se pridruziti ograniceni linearni funkcional 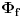 prostora prostora 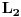 , (tj. vektor , (tj. vektor 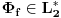 ) definisan na sledeci nacin: ) definisan na sledeci nacin: 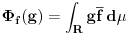 , pri cemu je samo preslikavanje , pri cemu je samo preslikavanje 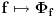 antilinearno i svakom vektoru pridruzuje vektor iste norme. Takodje, Pomenuto preslikavanje je bijektivno, pa je otuda antilinearno i svakom vektoru pridruzuje vektor iste norme. Takodje, Pomenuto preslikavanje je bijektivno, pa je otuda 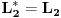 . No, ne vidim kakve veze to ima sa Parsevalovom jednakoscu. . No, ne vidim kakve veze to ima sa Parsevalovom jednakoscu.Ja to malo posmatram sa fizicarskog aspekta. U kvantnoj mehanici funkcija stanja koja daje svu informaciju o nekom kvantnom sistemu ne moze biti funkcija polozaja i impulsa zbog relacija neodredjenosti. Dakle imamo funkciju ili koordinata ili impulsa. Postulat km je da je ova funkcija iz  . Prelaz iz koordinatne u impulsnu reprezentaciju dat je preko FT. A ja volim da posmatram to na sledeci nacin: . Prelaz iz koordinatne u impulsnu reprezentaciju dat je preko FT. A ja volim da posmatram to na sledeci nacin: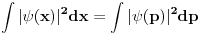 kao prelaz 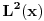 u u 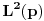 [ petarm @ 31.01.2009. 12:11 ] @
Ne vidim na sta ciljas?
[ Nedeljko @ 31.01.2009. 12:27 ] @
[ petarm @ 31.01.2009. 21:12 ] @
Ok! Dobija se da integral divergira. Za one slucajeve u KM nece ipak biti ovakvih problema jer su sve funkcije
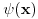 odnosno odnosno 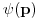 neprekidne ( neprekidne (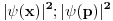 su gustine verovatnoce). Ipak ne bi bilo lose da ovo malo prodiskutujemo. Naravno ovim si mi pokazao da nije dovoljno kod ovog prelaza da kazem samo da je su gustine verovatnoce). Ipak ne bi bilo lose da ovo malo prodiskutujemo. Naravno ovim si mi pokazao da nije dovoljno kod ovog prelaza da kazem samo da je  iz iz  . Interesantno je da je ova fja i iz . Interesantno je da je ova fja i iz 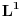 . Zanimljivo je takodje da Laplasova transformacija ove funkcije postoji . Zanimljivo je takodje da Laplasova transformacija ove funkcije postoji 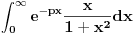 . Da li smatras da je pravilno reci ako za neku fju . Da li smatras da je pravilno reci ako za neku fju  FT npr. definisana kao FT npr. definisana kao 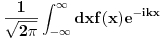 ne postoji treba mnoziti integrand sa ne postoji treba mnoziti integrand sa 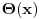 i svesti to na LT. i svesti to na LT. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|