Pođi od ove skice:

Tesko da mogu da ukapiram nacin resavanja ovih zadataka sa ovog grafika.

Još malo pomoći.
Ja ovu jednakost arccosX=aX+pi/2 zamišljam kao presječnu tačku funkcija
y=arccosx i y=ax+pi/2.Ova prva funkcija je inverzna od y=cosx.
Druga funkcija je zapravo pramen pravaca kroz tačku (0;pi/2), sa varijabilnim
koeficijentom smijera "a".Svi ovi pravci sijeku funkciju y=arccosx
barem jednom.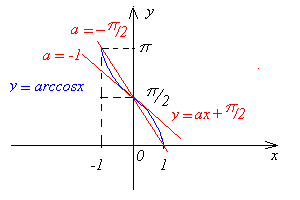

Da bi se išlo dalje treba znati:
-Vrijednost prvog izvoda funkcije y=arccosx za x=0, ili bar za y=cos x
za x=pi/2.
-Pod kojim uglom funkcija y=arccosx siječe y osu.Odatle jedna granica za "a".
-Područje definicije i konvenciju za vrijednost funkcije y=arccosx.Odatle druga
granica za "a".
-Da li je granica uključena u rješenje ili ne, tj "[" ili "(".


_{[Ovu poruku je menjao zzzz dana 24.01.2009. u 11:05 GMT+1]}