[ petarm @ 02.02.2009. 14:21 ] @
| Treba mi malo pomoci oko matematicke strogoce. Evo nesto na sta sam nabasao i moram priznati da me je zbunilo... Unapred hvala na odgovoru! |
|
[ petarm @ 02.02.2009. 14:21 ] @
[ Nedeljko @ 02.02.2009. 16:09 ] @
[ petarm @ 02.02.2009. 16:49 ] @
Ova tema pocinje s njim!
http://www.elitesecurity.org/t334007-0-Delta-distribucija [ Nedeljko @ 03.02.2009. 10:53 ] @
Kad govoris o ermitskim operatorima, onda radis u Hilbertovom prostoru. Sto se tice funkcionalnih prostora, takav je Lebegov prostor
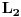 . No, proizvod . No, proizvod 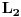 funkcije sa funkcije sa  ne mora obavezno biti ne mora obavezno biti 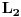 funkcija. Takodje, ovde radis u Lebegovom prostoru posecenom po relaciji "jednako skoro svuda". funkcija. Takodje, ovde radis u Lebegovom prostoru posecenom po relaciji "jednako skoro svuda".Zapravo, za merljiv prostor  i merljivu funkciju i merljivu funkciju  je proizvod funkcije je proizvod funkcije  sa ma kojom funkcijom iz sa ma kojom funkcijom iz  funkcija iz funkcija iz  akko je akko je  . Dakle, tebi u slucaju kada je . Dakle, tebi u slucaju kada je  merljiv podskup od merljiv podskup od  treba da funkcija treba da funkcija 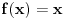 bude esencijalno ogranicena, a to je slucaj tacno onda kada je bude esencijalno ogranicena, a to je slucaj tacno onda kada je  ogranicen skup, a spektar je tacno zatvorenje skupa ogranicen skup, a spektar je tacno zatvorenje skupa  , pa je u tom slucaju spektar zaista i ogranicen. , pa je u tom slucaju spektar zaista i ogranicen.[ petarm @ 03.02.2009. 12:24 ] @
Ono sto mene jos zanima ako mozes da mi odgovoris je sledece. Dakle ta prekidnost se ogleda u tome sto mnozenjem
 sa nekom funkcijom sa nekom funkcijom 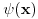 koja je iz koja je iz  mozes da dobijes funkciju koja nije iz mozes da dobijes funkciju koja nije iz  . Da li si ti to video odmah iz sv. problema: . Da li si ti to video odmah iz sv. problema: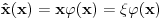 Posto se dobija  koja nije iz koja nije iz  . Odnosno da li je svaki operator s neprekidnim spektrom prekidan? . Odnosno da li je svaki operator s neprekidnim spektrom prekidan? I da li mozes da navedes primer neke neprekidne funkcije  iz iz  za koju vazi da za koju vazi da 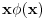 nije iz nije iz  ? ?Hvala na odgovoru! [ Nedeljko @ 03.02.2009. 13:55 ] @
 ne pripada prostoru ne pripada prostoru 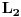 . Tu su samo merljive funkcije (dakle, obicne funkcije, ne distibucije), ciji je integral kvadrata modula konacan. . Tu su samo merljive funkcije (dakle, obicne funkcije, ne distibucije), ciji je integral kvadrata modula konacan.To sto mnozenjem funkcije koja pripada prostoru dobijas nesto sto ne pripada prostoru znaci da taj operator pre svega nije definisan u nekim tackama, bar sa tim izborom i kodomena, tj. da to uopste nije preslikavanje sa tim domenom i tim kodomenom. Funkcija 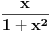 pripada prostoru pripada prostoru 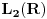 , ali funkcija , ali funkcija  ne pripada prostoru ne pripada prostoru 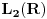 . .[ petarm @ 03.02.2009. 13:59 ] @
Citat: Nedeljko:  ne pripada prostoru ne pripada prostoru 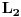 . Tu su samo merljive funkcije (dakle, obicne funkcije, ne distibucije), ciji je integral kvadrata modula konacan. . Tu su samo merljive funkcije (dakle, obicne funkcije, ne distibucije), ciji je integral kvadrata modula konacan.Citat: petarm: Ono sto mene jos zanima ako mozes da mi odgovoris je sledece. Dakle ta prekidnost se ogleda u tome sto mnozenjem  sa nekom funkcijom sa nekom funkcijom 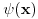 koja je iz koja je iz  mozes da dobijes funkciju koja nije iz mozes da dobijes funkciju koja nije iz  . Da li si ti to video odmah iz sv. problema: . Da li si ti to video odmah iz sv. problema: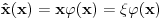 Posto se dobija  koja nije iz koja nije iz  . . To sam i rekao! Citat: Nedeljko: To sto mnozenjem funkcije koja pripada prostoru dobijas nesto sto ne pripada prostoru znaci da taj operator pre svega nije definisan u nekim tackama, bar sa tim izborom i kodomena, tj. da to uopste nije preslikavanje sa tim domenom i tim kodomenom. Funkcija 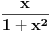 pripada prostoru pripada prostoru 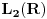 , ali funkcija , ali funkcija  ne pripada prostoru ne pripada prostoru 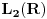 . .Hvala! [ Nedeljko @ 03.02.2009. 14:03 ] @
Mnozenjem merljive funkcije sa x ne mozes dobiti Dirakovu distribuciju, vec merljivu funkciju.
[ petarm @ 04.02.2009. 14:20 ] @
[ Nedeljko @ 04.02.2009. 16:13 ] @
Ne mozes kao sopstveni vektor dobiti nesto sto nije vektor, tj. sto ne pripada tom prostoru. Nikakva
 distribucija ne pripada Lebegovom prostoru. Dirakovu distribuciju mozes dobiti iskljucivo ako radis problem sopstvenih vrednosti operatora u prostoru Distribucija, ali to nije Hilbertov prostor, pa ne mozes govoriti o samoadjungovanosti. Moras imati kompletnu korektnu formulaciju zadatka, a ne samo neke parcice, inace dobijas matematiku poput fizike nekih ucesnika teme o teoriji relativnosti foruma za fiziku ES-a. distribucija ne pripada Lebegovom prostoru. Dirakovu distribuciju mozes dobiti iskljucivo ako radis problem sopstvenih vrednosti operatora u prostoru Distribucija, ali to nije Hilbertov prostor, pa ne mozes govoriti o samoadjungovanosti. Moras imati kompletnu korektnu formulaciju zadatka, a ne samo neke parcice, inace dobijas matematiku poput fizike nekih ucesnika teme o teoriji relativnosti foruma za fiziku ES-a.U prostoru distribucja je za ma koju beskonacno diferencijabilnu funkciju  korektno definisan linearan operator korektno definisan linearan operator  sa sa 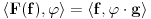 U slucaju da je U slucaju da je 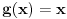 , sopstveni vektor tog operatora je Dirakova distribucija, ali prostor distribucija ne obrazuje Hilbertov prostor, pa ovaj slucaj ne odgovara formulaciji tvog zadatka u kome se pominje pojam smoadjungovanog operatora. , sopstveni vektor tog operatora je Dirakova distribucija, ali prostor distribucija ne obrazuje Hilbertov prostor, pa ovaj slucaj ne odgovara formulaciji tvog zadatka u kome se pominje pojam smoadjungovanog operatora.[ petarm @ 05.02.2009. 16:17 ] @
[ Nedeljko @ 06.02.2009. 07:52 ] @
Definisi mi taj Rigid Hilbert space.
[ petarm @ 06.02.2009. 18:52 ] @
[ Nedeljko @ 07.02.2009. 15:09 ] @
Ja tamo vidim samo neku svađu. Da li bi mogao da napišeš formalnu definiciju od RHS?
[ petarm @ 08.02.2009. 11:49 ] @
[ Nedeljko @ 09.02.2009. 10:35 ] @
Ako je
 gust Hilbertov potprostor Hilbertovog prostora gust Hilbertov potprostor Hilbertovog prostora 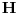 , onda je , onda je  . Pravis li razliku izmedju predhilbertovog prostora (vektorskog prostora sa skalarnim proizvodom) i Hilbertovog prostora (kompletnog predhilbertovog prostora)? . Pravis li razliku izmedju predhilbertovog prostora (vektorskog prostora sa skalarnim proizvodom) i Hilbertovog prostora (kompletnog predhilbertovog prostora)?Kompletan potprostor normiranog prostora je uvek njegov zatvoren potprostor, a zatvoren gust potprostor normiranog potprostora je ceo prostor. Cak i u slucaju da je  , sta ti je , sta ti je 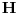 , tj. koji Hilbertov prostor? , tj. koji Hilbertov prostor?Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|