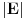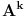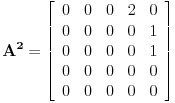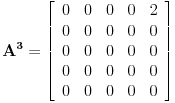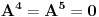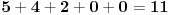[ LSDCracker @ 10.02.2009. 19:15 ] @
| Ok, ja imam jedan problem, a to je.... Kako izracunati maksimalan broj putanja na nekom grafu? Sad ne znam koliko bi vama koristilo da vam pastam kod iz c-a, al svejedno jedini problem koji pravi kod generisanja puteva jeste taj koliko zapravo putanja moze biti. Trenutno sa cim program moze da mi radi je kad je graf jedna linija na kojoj se nalazi nekoliko tacaka stim da su povezane 1-2-3-4-5 Odnosno putevi koji se nalaze na grafu su : 1-2 2-3 3-4 4-5 Graf je usmeren pa je zapravo (1->2, 2->3...) I sad maksimalan broj puteva koji se mogu generisati je lako naci... 5*4/2 I onda mi on generise sve putanje 1-2 2-3 3-4 4-5 1-3 2-4 3-5 1-4 2-5 1-5 Ali... Zelim drugaciji raspored puteva... recimo ovakav slucaj : 1-2 1-3 2-4 3-4 4-5 Onda imamo dve grane koje krecu iz keca prema 2 i 3 a onda se te dve grane spajaju u 4 a iz 4 ide u 5. Ali broj puteva zavisi od slucaja do slucaja kako sam gledajuci od slucaja do slucaja zakljucio. Nego ne mogu da nadjem nacin kako se izracunava maksimalan broj puteva na jednom grafu. Tacke koje imaju 0 grana me ne interesuju i nisu bitne za moj algoritam. Sad program je napravljen tako da generise puteve dok god ne nadje maksimalan broj puteva koji se mogu naci stim da su svi razliciti. Sad... Jel postoji nacin da se za opsti graf nadje maksimalni broj puteva koji se mogu generisati pomocu predifisanog grafa? |