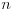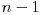Po definiciji ne mogu i to je odgovor kad te neko pita. Ja sam vidjao neke pokusaje gde se cetvrta dimenzija predstavlja bojom.

Hm, ako se na papiru (2D) moze predstaviti kocka (3D) (projekcijom), zasto se ne bi hiperkocka (primer) mogla porjektovati u 3D, zatim dobijeno u 2D (na papir/ekran/whatever)?

Zato sto ne znamo kako izgleda :)

OK, hvala. Znaci geometrijska interpretacija=nacrtati.

Evo je kocka u 4d :)

Bravo! Upravo tako, a projekcijama se bavi projektivna geometrija (nacrtna). Tako da teoretski jeste moguće napraviti projekciju 4D tela u 3D. Kako to izvesti praktično, druga je stvar. Mislim da sam svojevremeno video mašine za sečenje koje kontrolišu računari, i one bi bile najpribližnije izradi projekcija u 3D.

Ova animacija bi bila projekcija projekcije.

Idući tom logikom onda bi mogli u (1D) predstaviti sliku iz (2D), a onda dalje
iz (1D) u (0D).I buljeći u takvu tačku razaberemo u njoj neki geometrijski lik.

I zzzz i ostali su donekle u pravu.

Prostorni lik nije jednoznačno određen njegovom projekcijom u ravni, a jezik nacrtne geometrije obezbeđuje na crtežu dodatne informacije (osim projekcije) o projektovanim tačkama, da bi se prostorni lik mogao rekonstruisati.

Dodatne informacije "jezika" nacrtne geometrije su još dve projekcije t.j. ukupno tri projekcije na tri ortogonalne ravni.

Naravno, ovo sam i ja imao na umu. Kompletna informacija se može dobiti posmatranjem 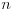projekcija dimenzije 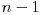. A i ovo verovatno samo za konveksna tela, inače projektivno preslikavanje nije bijektivno. Lupam, nisam još položio Nacrtnu.

Projekcija četvorodimenzionalne kocke

Dosta su ti i dve projekcije, ali možeš proći i jeftinije sa jednom projekcijom + još nešto sitno (manje od još jedne projekcije). Videti razne metode projektovanja (metodu odstojanja, centralno projektovanje itd). Recimo, kod metode odstojanja imaš još i informaciju o z-koordinati svake projektovane tačke, ako ti je papir u ravni Oxy (projekcije na z-osu se nanose na posebnu pravu).

Čovek je rekao da uči nacrtnu geometriju i projektovanje koje se upražnjava u arhitekturi, građevinarstvu, mašinstvu, elektrotehnici i sl.,
a tu su retko kad dovoljne dve projekcije, ponekad čak ni tri ne pokazuju odmah jasno predmet koji je projektovan nego je potrebna čak
i kosa projekcija upravo kao kod kocke gde sve tri ortogonalne projekcije daju jednak kvadrat. I gore prikazana projekcija četvorodimenzionalne
kocke je kosa projekcija jer bi bilo koja ortogonalna projekcija te kocke bila jednaka trodimenzionalna kocka.

U opštem slučaju je dovoljna jedna projekcija + još nešto sitno (npr. prava sa odstojanjima). Položio sam nacrtnu geometriju i znam šta su metode projektovanja.

Koliko bi ti takvih pravih trebalo za prikaz nekih jednostavnijih prodora ili senki. U praksi tako niko ne radi.

Dovoljna je jedna.

Druga stvar je koliko bi taj crtež bio jednostavan za čitanje, ali bise iz njega svakako moglo sve rekonstruisati.

Gde bi ta jedna stajala i kako?

Sa strane crteža (tj. nije deo projekcije), posebno obeležena, izigrava z-osu i na njoj su nanesene projekcije tačaka ne z-osu, naravne pod pretostavkom da je projekcija u Oxy ravni.

Dakle, na z osu su ustvari nanete kote tačaka koje su projektovane u 0xy ravan. Kote označavaju udaljenost
stvarnih tačaka od ravni 0xy. Jesam li razumeo?

Mislim da jesi. Odatle se sve može rekonstruisati, a koliko je pregledno i praktično, to je druga stvar.

Niti je praktično niti pregledno. Ovo čak nije ni planimetrijsko prikazivanje prostornih oblika kao što se,
na primer, prikazuje geografska konfiguracija terena. Ovo je samo jedna dozlaboga kilava mogućnost
koja se u praksi ne primenjuje ili izuzetno retko.Ovakav prikaz bi bio manje pregledan od tabelarnog, a
o vizuelnoj prostornoj predstavi da i ne govorimo jer je apsolutno i nema.

Pa, imaš projeciju na Oxy ravan, što jeste slično geografskim kartama (ali ne i isto zbog izohipsi). Da je gore od tabelarnog prikaza je preterivanje, a da za praksu nije idealno, slažem se.

Kako bi , na primer, prikazao rotacioni elipsoid na taj način?

_{[Ovu poruku je menjao galet@world dana 03.03.2009. u 14:58 GMT+1]}

U opštem slučaju, uvek možeš tako da predstaviš poliedar. Da projektuješ možeš sve, a kod elipsoida predstavi precizno nekoliko ključnih tačaka iz kojih se može rekonstruisati elipsoid ako se zna šta predstavljaju.

Pričam ti priču. Pa hajde pokaži!

Šta da pokažem?

Pa rotacioni elipsoid na taj tvoj jednostavniji način.

Krug sa obeleženim centrom (kao O i A), sa obeleženim "temenima" kruga (dve tačke B i C na krugu za koji je ugao BOC prav), sa z-osom na kojoj su tačke O,B i C u nultoj tački, a tačka A izvan nule i sa opisom šta znače tačke O,A,B i C.

O kom jednostavnijem načinu pričaš?

.

O ovom:

Je li ovo to "sitno":

A kakav bi bio opis ako konture tela nisu matematički definisane i kako bi Kinez pročitao taj tvoj opis ili je to neki nacionalni srpski prikaz?
Nedeljko ne pričaj koještarije. Prikaz tela mora biti jasan na svim jezicima sveta i bez tekstualnog objašnjenja.

Kod tebe se projektovanje svodi na pričanje. Što nisi nacrtao t. j. prikazao rotacioni elipsoid ovde po toj
tvojoj "sitnoj" metodi pa da vidimo prednosti te metode?
Ili, ako ti je lakše, prikaži neki torus ili neki pobednički pehar ili čašu s jednom "nogom", a mi da pogađamo šta si
prikazao. Bilo bi interesantno.

I gde sam pomenuo jednostavnost? Minimalizam je obično suprotstavljen jednostavnosti.

Kako misliš da proizvoljno telo prikažeš konačnim brojem projekcija? Ono što može je da se ograničiš na neku klasu tela, npr. poliedre i onda ti ne trebaju nikakva dodatna tekstualna objašnjenja.

Samo ti prikaži neko od predloženih tela na taj način - naravno ako umeš pa da vidimo.
Pusti priču.

Šta, sad je sporno da se poliedar može tako prikazati?

Ne eskiviraj nego prikaži neko od predloženih tela! I ne mora biti poliedar.