Jel mi moze neko objasniti kako se rade ovi oblici integrala?

∫(dx/(a+bx^2))

i

∫(dx/(ax^2+bx+c))


Hvala unapred!

Nemam vremena da opsirno odgovorim, ali evo ukratko.

Integrali funkcija oblika

f(x) = P_m(x)/P_n(x)

gde je P_m polinom m-tog stepena se resavaju na sledeci nacin:

1. ako je m>=n, prvo se polinomski podeli P_m sa P_n pa se time svede na slucaj 2.

2. ako je m<n, ovo je tvoj slucaj

- polinom u imeniocu se nasteluje/dopuni konstantom da u njemu imas zbir/razliku kvadrata.
- u zavisnosti od onoga sto ostane pored, integral se onda svede na tablicni integral kome je resenje oblika k*arctg(mx+n) ili k*ln(mx+n),
a to zavisi od toga da li podintegralnu funkciju na kraju svedes na 1/(x² + 1) ili na 1/(x² - 1)

Tvoji zadaci:

1. Ovo je vec gotovo reseno:

∫dx/(a+bx²) =
1/a * ∫dx/(1 + b/a*x²) =
1/a * ∫dx/(1 + (sqrt(b/a)*x)²) =
1/a * 1/sqrt(b/a) * ∫d(sqrt(b/a)*x)/(1 + (sqrt(b/a)*x)²) = (ovo je kao da si uveo smenu t=sqrt(b/a)*x)
1/a * 1/sqrt(b/a) * arctg (sqrt(b/a)*x) =
1/sqrt(ab) * arctg (b/a * x)

2. ∫dx/(ax² + bx + c) =
1/a * ∫dx/(x²+ b/ax + c/a) =
1/a * ∫dx/((x+b/2a)² - (b/2a)² + c/a =
1/a * ∫dt/(t² - ... )

Mozda bi mogao i da diskutujes vrednosti a, b i c, pa da u zavisnosti od toga dobijas resenje oblika k*arctg(mx) ili k*ln(mx)

etc.

Prvi sam skontao, ako bi neko mogao malo bolje ovaj drugi da objasni ?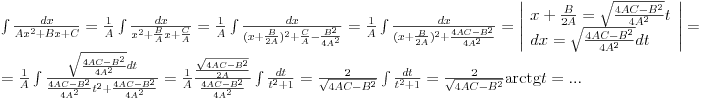

Jel sad dovoljno dobro?

Sad je dobro... Hvala puno!

Moze li neko da mi objasni kako je iz ovog 9∫1/x^2dx dobijeno -9/x+c,
laik sam za integrale, bolje receno, nemam pojma. Ceo zadatak glasi ovako,

∫((2x+3)^2/x^2)dx=
∫(4x^2+12x+9/x^2)dx=
∫(4+12x+9/x^2)dx=
4∫dx+12∫xdx+9∫1/x^2dx=
4x+12ln[x]-9/x+c

sve ostalo razumem, osim tog zadnjeg, i mozda nije za ovu temu, ali da ne postavljam novu. HVALA

Apsen je majka za ovo. Ne slušaj one koji kažu da nije dobar. Za integrale je super!

Dakle, potraži knjige i zbirke Borisa Apsena (izdaje Školska knjiga Zagreb).