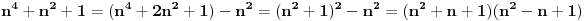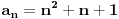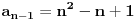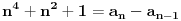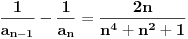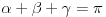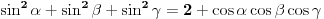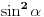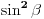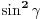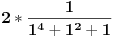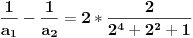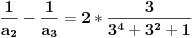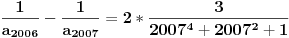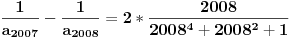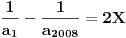zadaci-pokusala,ne ide...Hitnooo

[ Adnaaa @ 22.02.2009. 21:10 ] @

1.zadatak:

Izracunati sumu :

1/(1^4 + 1^2 + 1) + 2/(2^4 + 2^2 + 1 ) + ... + 2008/ ( 2008^4 + 2008^2 + 1 )

Ne znam jesam li pravilno napisala ali ovo 1^4 je jedan na cetvrtu.

2.zadatak :

Ako za uglove a,b,c trougla vrijedi :

sin^2 a +sin^ b + sin ^c = 2
dokazi da je trougao pravougli.

3.zadatak :
Ako su p i (p^2 + 8) prosti brojevi,dokazi da je i (p^2 + 4) prost broj.

Hitno mi je potrebna pomoc za ove zadatke.
HVALLAAAA

A evo i mog pokusaja,vise puta sam pokusala rastaviti,ali ne znam kako zavrsiti :

1/3 +1/3 * 2/7 + 1/7 *3/13 +...+

a pokusala sam i ovako rastaviti ali ne dobijem konacan rezultat

2008^4 + 2008^2 +1 = 2008(2008^3+2008 + 2008^-1)

i onda se skrati 2008 u brojniku i nazivniku i ostane :
1/ 2008^3 + 2008 +2008^-1

Je li ispravan ijedan od ovih nacina,ili da pokusam na drugi ?

[ Nedeljko @ 23.02.2009. 16:35 ] @

1. Zadatak:

Uz oznaku

važi

, odnosno

. Stoga je

. Dalje bi trebalo da znaš sama.

2. Zadatak.

Iskoristi vezu zimedju ugla, naspramne stranice i prečnika opisanog kruga (sinusna teorema). Zatim vidi kakav je odnos između prečnika opisanog kruga i najduže ivice trougla kod pravouglog, tupouglog i oštrouglog trougla.

[ Nedeljko @ 24.02.2009. 07:18 ] @

Što se tiče drugog zadatka, uz uslov

pokazuje se da je

.

Prvo se

prikazu preko kosinusa dvostrukog ugla, a

se prikaže preko kosinusa istog ugla, pa se zbir dva kosinusa pretvori u proizvod, iskoristi veza između bilo kog ugla u zbira druga dva ugla itd.

[ Adnaaa @ 26.02.2009. 21:15 ] @

Neizmjerno Vam hvala za ovo... :)

A mozete li mi reci kako da dovrsim ovaj 1.zadatak,evo pokusavam...

u ovo a(n-1)=n^2-n+1
a (n)=n^2+n+1

je li se u oba izraza uvrsti n,ili ide u prvi n-1,a u drugi n?
I kako ukopiti ovo u prvu jednacinu,postavku zadatka ?
Unaprijed zahvalna

[ Adnaaa @ 26.02.2009. 22:02 ] @

Izvinjavam se,dosla sam do rjesenja.
Posto je gore 2n/n^4+n^2+1

onda citav izraz pomnozim sa 2.Ako rjesenje oznacim sa x,onda kad pomnozim biti ce 2x.
Ovo sam pomnozila jer je u zadatku dato n/n^4+n^2+1
a prilikom rastavljanja potrebno je 2n/n^4+n^2+1.
I kada dobijem konacno rjesenje podijelim sa 2 da bi dobila x.
Konacan rezultat izadje 403407/8068144
Jesam li upravu ?

[ h4su @ 26.02.2009. 22:26 ] @

Kako je Nedeljko vec napisao iskoristis ovo :

pa imas

2=

za n=2

za n=3

...
za n=2007

za n=2008

Kad to sve saberes imas: 2+

.

_{[Ovu poruku je menjao h4su dana 27.02.2009. u 09:57 GMT+1]}