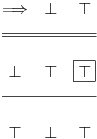
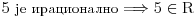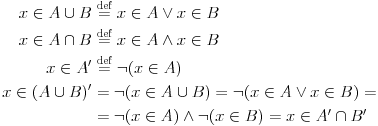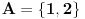[ Cabo @ 27.02.2009. 16:23 ] @
|
[ h4su @ 27.02.2009. 20:18 ] @
Pa vrlo jednostavno npr iz pretkostavke da je 1=2 sto nije tacno slijedi da je 3=3 sto je jel tacno.
1=2 1+2=2+1 [ Cabo @ 01.03.2009. 20:24 ] @
[ cozi @ 01.03.2009. 21:53 ] @
p->q je sud koji znaci ako p onda q. iskaz p ti je antecedens a iskaz q je konsekvens.
Standardni primer je: pada kisa (p) , ulice su mokre (q). Ako je istina da pada kisa, onda je istina da su i ulice mokre. Ako nije istina da kisa pada, taj iskaz tada ne govori nista o ovom drugom iskazu, ulice mogi biti i mokre i ne moraju... tj. pravilnim zakljucivanjem, na neki drugi nacin, se moze doci do ispravnog zakljucka. Dakle ako ne vazi p onda do istinosti q dolazis na neki dugi nacin. Tako je moguce da iz neistinitog iskaza sledi istinit. Iz iskaza p->q i iskaza p (tj. znati da je p istinito) moze se zakljuciti (pravilom zakljucivanja modes ponens) q. Dakle ako je iskaz q istinit istinitost iskaza p u implikaciji nije vazna za njegovu istinitost. Cinimi se da ti mislis da je iskaz q u implikaciji zakljucak iskaza p, pa ti je cudno kako iz neistinitog iskaza moze se zakljuciti istinit. U ovom (tvom) primeru, ako je 5 realan broj (a jeste) za istinitost tog iskaza nije bitno sta je prethodni iskaz. Implikacija p->q je takodje iskaz, za istinitost tog (celog iskaza) bitno je i istinitost iskaza i p i q. Implikacija nije tacna jedino ako iz tacnog iskaza sledi netacan iskaz. [ Nedeljko @ 02.03.2009. 07:24 ] @
Ja lično ne vidim smisao obrazlaganja definicija, sem kada treba proveriti njihovu korektnost.
Ako želiš iskazni veznik koji ima istinitosnu vrednost tačno akko su operandi jednaki, takav veznik već postoji i zove se ekvivalencija. Nije implikacija uperena protiv ekvivalencije, nego su oba veznika u upotrebi, svaki za svoju svrhu. [ Cabo @ 02.03.2009. 16:50 ] @
Citat: Nedeljko: Ja lično ne vidim smisao obrazlaganja definicija, sem kada treba proveriti njihovu korektnost. Upravo je poenta u smislu. Ne volim kada pričam o nečemu što ne shvatam. Za to služe primeri, a ja sam u prvoj poruci ove teme upravo tražio iste. Primeri su „meso“ Matematike, bez njih nema učenja ničega, pa ni Matematike. Nevezano sa temom, mislim da je upravo ovakav stav krivac za relativno slabo poznavanje Matematike u Srbiji. Dok ne shvatimo da bez nastave nema nauke to stanje se neće popraviti. Ja studiram ovoliko dugo između ostalog i zbog takvog stava profesora, koji teraju tu „naučnu“ priču nauštrb nastavne. Ispod časti im je da se spuštaju na nivo studenata i zaista objasne, najbolje primerima, pojam ili koncept o kome pričaju. [Ovu poruku je menjao Cabo dana 02.03.2009. u 18:02 GMT+1] [ Nedeljko @ 02.03.2009. 17:40 ] @
Citat: Cabo: Upravo je poenta u smislu. Onda nisi razumeo pojam definicije. Niko ti ne brani da sačiniš kakvu god hoćeš istinitosnu tablicu i taj veznik obeležiš nekim simbolom i nazoveš nekim imenom. Dok ne budeš shvatio fundamentalne koncepte u koje spada i pojam definicije, nemoj da se čudiš ako ti slabo ide. Ako neko nije zadovoljan ovakvim odgovorom, onda to znači da nije dobro formulisao pitanje. Ako je hteo da pita gde se implikacija koristi u matematici, onda pitanje treba tako da glasi. Ako je hteo da pita nešto treće, onda treba pitanje da postavi tako da ga drugi razumeju. [ miki069 @ 02.03.2009. 22:01 ] @
p je "3 je delilac broja 7"
q je "3 je delilac od 3*7=21". p==>q je tačno. Jel tačna implikacija (p i q) ==> r ??? Gde su: p je "Ribe žive u vodi" q je "Slonovi nisu ribe" r je "Slonovi ne žive u vodi". [ maksvel @ 02.03.2009. 22:24 ] @
Hehe, ovo potonje bi bio kao neki silogizam anti-sofizam
[ miki069 @ 02.03.2009. 22:43 ] @
Ne znam Marjane ni sad odgovor.
Profa nam je tako počeo predavanje iz Logike - pitanjem. Svi smo rekli da je tačna implikacija, al nas on onda zaskočio sa rakovima. 2 časa ništa nije predavao dok nas nije sve "ubedio" da nije tačno - zbog rakova, vodenih zmija, aligatora... Mi morali da pokleknemo. Davno je to bilo 1987 - nema demokratske većine.... Ni sad ne znam odgovor. Pozdrav [ Nedeljko @ 03.03.2009. 11:03 ] @
Ja bih taj primer sa slonovima formalizovao kroz predikatski račun.
Šema zaključivanja odgovara zatvorenoj predikatskoj formuli (rečenici) 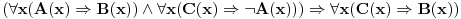 , ,Ova formula nije valjana, jer postoje modeli u kojima nije tačna. recimo, ako je domen 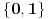 , , 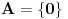 , , 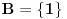 , , 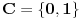 , onda u toj interpretaciji navedena formula svakako nije tačna, pa navedeno zaključivanje nije dobro. , onda u toj interpretaciji navedena formula svakako nije tačna, pa navedeno zaključivanje nije dobro.Međutim, postoje interpretacije u kojima je navedena rečenica tačna (kao ona sa slonovima) u kojoj je gornja formula tačna, bez obzira što samo logičko zaključivanje nema opravdanje u logici (nije u pitanju valjana formula, tj. shema nije u opštem slučaju ispravna). [ Cabo @ 04.03.2009. 13:52 ] @
Citat: Nedeljko: Onda nisi razumeo pojam definicije. Niko ti ne brani da sačiniš kakvu god hoćeš istinitosnu tablicu i taj veznik obeležiš nekim simbolom i nazoveš nekim imenom. Dok ne budeš shvatio fundamentalne koncepte u koje spada i pojam definicije, nemoj da se čudiš ako ti slabo ide. Ako neko nije zadovoljan ovakvim odgovorom, onda to znači da nije dobro formulisao pitanje. Ako je hteo da pita gde se implikacija koristi u matematici, onda pitanje treba tako da glasi. Ako je hteo da pita nešto treće, onda treba pitanje da postavi tako da ga drugi razumeju. Razumeo sam ja vrlo dobro pojam definicije, ali su definicije i teoreme same po sebi ništa bez primera. Koji je smisao definicije ako se ona nigde ne koristi? Primene daju smisao matematici. Ovo je i ključna tačka po kojoj se matematika koja se radi u Srbiji razlikuje od „svetske“. Mi se bavimo dubokoumnom i suvoparnom teorijom koja, bar prema onome što se može zaključiti na osnovu stanja u nastavnoj praksi, nema svrhu i smisao. U svetu nije tako, i velika pažnja se posvećuje upravo primenama matematike. Lično smatram da je to ispravan cilj nekih budućih reformi matematike kod nas. Nisi me razumeo, odgovorom h4su-a sam zadovoljan, a i sam sam naveo primer koga sam se u međuvremenu setio. [ cozi @ 04.03.2009. 16:08 ] @
Ako si zadovoljan odgovorom h4su-a onda, meni se cini, ti nista nije jasno.
Ako hoces da polozis logiku onda ne trazi nikakve primere za definicije, ne pokusavaj da razumes i sl. jednostavno nauci pravila i koristi ih, dosledno. Logika je takva; ne znam kakav primer ocekujes za sledecu definiciju: skup osnovnih simbola se obicno zadaje nabrajanjem ili individualne promenljive i indivudualne konstate su termi.... Smisao definicija u logici je izgradnja jednog formalnog sistema, odredjivanje formalnog jezika... da bi se izbegle dovsmislenosti, protivurecnosti, nepreciznosti... stoga su i definicije striktne i tako se i primenjuju... -> implikacija, je logicki veznik, za koji postoje odrednja pravila i to je to. U mom prethodnom postu imas pojasnjenja, jos jedanputa cu naglasiti ,ono sto mi se ucinilo iz prvog posta da ti nije najjasnije, konsekvens nije zakljucak iz antecedensa. q nije zakljucak iz p, niti su ekvivalentni. [ Nedeljko @ 05.03.2009. 07:53 ] @
Mislim da si malo preterao. Da, primene su zaista bitne, ali se pitanje pokretača teme nije odnosilo na problem sa primenom tablice implikacije. Da je on naveo zadatak u kome mu korak sa primenom tablice nije jasan, onda bi u odgovoru to moralo da se objasni. Da je pitao šta će mu implikacija u matematici i na to bi mogao da dobije vrlo konkretan odgovor. Međutim, treba umeti pitati ono što ti nije jasno. Ako pitaš da ti neko objasni tablicu uvedenu definicijom, onda ti pojam definicije nije jasan.
[ Cabo @ 06.03.2009. 15:13 ] @
Citat: Nedeljko: Mislim da si malo preterao. Da, primene su zaista bitne, ali se pitanje pokretača teme nije odnosilo na problem sa primenom tablice implikacije. Da je on naveo zadatak u kome mu korak sa primenom tablice nije jasan, onda bi u odgovoru to moralo da se objasni. Citat: Cabo: Može li neko da da primer logičkog iskaza koji ovo ilustruje (da netačno implicira tačno)? No comment. [ Cabo @ 06.03.2009. 15:18 ] @
Citat: cozi: Logika je takva; ne znam kakav primer ocekujes za sledecu definiciju: skup osnovnih simbola se obicno zadaje nabrajanjem ili individualne promenljive i indivudualne konstate su termi.... Čekaj, da li smo se dobro razumeli? Logika nema svrhu? Očito tebi nije jasno da svaki predmet ima svoju svrhu i da za svaku, pa i za ovu koju si ti naveo, definiciju i teoremu postoji bar nekoliko primera. [ Nedeljko @ 06.03.2009. 18:20 ] @
Citat: Cabo: No comment. Primer je bolo koje tvrđenje oblika A=>B, gde je A netačan, a B tačan iskaz. Na primer, "Mesec je na Suncu => Zemlja nije ravna", ali ti on neće pojasniti zašto je tablica takva kakva jeste. Ako neko hoće tablicu u kojoj netačno nije u relaciji sa tačno, takva tablica već postoji i odgovarajući veznik se zove ekvivalencija. No, to ne znači da je implikacija u pravu, a da je ekvivalencija pogrešna, već da se radi o različitim veznicima, koji samim tim imaju različite upotrebe. Da je pitanje glasilo "Kada se upotrebljava implikacija?", mogao bi se dati konkretan odgovor. Citat: Cabo: Čekaj, da li smo se dobro razumeli? Logika nema svrhu? Očito tebi nije jasno da svaki predmet ima svoju svrhu i da za svaku, pa i za ovu koju si ti naveo, definiciju i teoremu postoji bar nekoliko primera. Hajde, reci ko je rekao da logika nema svrhu. Da, formalna je pa šta, kao što je i cela matematika formalna, ali to ne znači da su neprimenljive. Kada se razumeju njihove suštine, onda se zna i kako se primenjuju. [ maksvel @ 06.03.2009. 18:28 ] @
Ja se sećam da je profa u srednjoj školi za implikaciju dao "objašnjenje" za N -> T = T tipa "Dobro je kada se od neistine dođe do istine"
BTW, evo jedan interesantan link koji sam našao u međuvremenu: http://www.jcu.edu/philosophy/gensler/fe/fe-0--01.htm [ Nedeljko @ 06.03.2009. 18:44 ] @
Profa ti je stvarno faca. Zanimljivo je, a ima i dubinu.
[ h4su @ 06.03.2009. 19:10 ] @
Kako sam ja shvatio cabo je u jednom momentu dosao do dileme kako iz netacnog moze ispravnim zakljucivanjem doci do tacnog i dobio je odgovor na to pitanje.Sta je definicija, implikacija, ekvivlencija i sl. nije tema danasnje emisije bar ja nisam tako shvatio.
Citat: cozi: Ako hoces da polozis logiku onda ne trazi nikakve primere za definicije, ne pokusavaj da razumes i sl. jednostavno nauci pravila i koristi ih, dosledno. Cozi je nesto pricao o bubanju napamet. [ cozi @ 06.03.2009. 19:32 ] @
Citat: Cabo: Čekaj, da li smo se dobro razumeli? Logika nema svrhu? Očito tebi nije jasno da svaki predmet ima svoju svrhu i da za svaku, pa i za ovu koju si ti naveo, definiciju i teoremu postoji bar nekoliko primera. Ne, nisam rekao da nema svrhu, samo sam naglasio formalni karakter logike i njenu striktnost. Kakva je svrha logike? O tome ne bih ni raspravljao, logika je nastala kao deo Aristotelovog filozofskog sistema, pa bez posznavanja celog sistema ne znam kako bi raspravljali o tome. Cinimi se da je u savremena logika izjednacava svrhu sa primenom, ne znam o tome, previse pa ne bi ni o tome... U pravu si, nije mi jasno da svaki predmet ima svrhu, to je vec metafizicka rasprava, postoje i filozofi koji ne smatraju da je to slucaj, postoje i oni koji ne smatraju. U svakom slucaju to se ne moze znati, samo mozes verovati... (Nadam se da nisi mislio na skolski predmet) U formalnim teorijama definicija je pravilo kojim se u formalni jezik uvodi novi simbol. I postoje 2 uslova za def. u logici, da su otklonjive i nekreativne. Tako ne vidim svrhu obrazlaganja def. Teoreme nisam pominjao. A skup teorema se obicno zadaje induktivnim definicijama... Postoji primer i za definiciju: iskaz a=a vazi apriori, primer je b=b, jel ti sta jasnije iz primera? Ne moze se sve egzemplarno uciti. Nisam govorio o bubanju napamet ali istinitosne tablice ne mogu se drugacije nauciti, kao ni pravila uvodjenja ili oslobadjanja i sl. Da mislim da treba da se buba ne bih dva puta obrazlagao implikaciju... [ Cabo @ 07.03.2009. 17:52 ] @
U knjizi „Matematička logika“ od Slobodana Vujoševića sam našao sledeću teoremu:
 Dakle, osobina da „netačno povlači proizvoljno“ se dokazuje. Citat: cozi: Ne, nisam rekao da nema svrhu, samo sam naglasio formalni karakter logike i njenu striktnost. Kakva je svrha logike? O tome ne bih ni raspravljao, logika je nastala kao deo Aristotelovog filozofskog sistema, pa bez posznavanja celog sistema ne znam kako bi raspravljali o tome. Cinimi se da je u savremena logika izjednacava svrhu sa primenom, ne znam o tome, previse pa ne bi ni o tome... Jedna svrha Logike koja mi se nameće ovako „na prvu loptu“, recimo, je da opiše Matematiku na formalno prihvatljiv i neprotivurečan način, u stepenu u kojem je to moguće učiniti. Citat: cozi: U pravu si, nije mi jasno da svaki predmet ima svrhu, to je vec metafizicka rasprava, postoje i filozofi koji ne smatraju da je to slucaj, postoje i oni koji ne smatraju. U svakom slucaju to se ne moze znati, samo mozes verovati... (Nadam se da nisi mislio na skolski predmet) Mislio sam i na fakultetske, i na školske predmete, a ta moja konstatacija bi se mogla proširiti i na nauku uopšte. Ako nešto nema svrhu, zašto se uopšte baviti time? Citat: cozi: U formalnim teorijama definicija je pravilo kojim se u formalni jezik uvodi novi simbol. I postoje 2 uslova za def. u logici, da su otklonjive i nekreativne. Nije mi jasan onaj deo o „otklonjivosti i nekreativnosti“. Jesu li to neki formalni izrazi ili neformalne vrednosne ocene? Citat: cozi: Postoji primer i za definiciju: iskaz a=a vazi apriori, primer je b=b, jel ti sta jasnije iz primera? Jeste, ali je definicija sama po sebi trivijalna, pa ovaj konkretni primer tvog stava o upotrebi primera u shvatanju smisla definicije nije ilustrativan. Citat: cozi: Ne moze se sve egzemplarno uciti. Može, i upravo je učenje preko primera pravi način da se bilo šta stvarno nauči. To se radi iz Metodike, Pedagogije... Citat: cozi: Nisam govorio o bubanju napamet ali istinitosne tablice ne mogu se drugacije nauciti, kao ni pravila uvodjenja ili oslobadjanja i sl. Da mislim da treba da se buba ne bih dva puta obrazlagao implikaciju... Mehaničkim bubanjem se dobijaju generacije koje ili imaju „kečeve“ iz Matematike ili „nemaju pojma“ kad krenu da rade a treba da praktično primene znanje iz Matematike, jer ne shvataju suštinu. Mora biti i primera, tako se radi svuda u svetu, a naročito po Bolonjskoj deklaraciji. [ cozi @ 07.03.2009. 20:18 ] @
Po drugi put, teoreme nisam spominjao, govorio sam o definicijama, a ti si postavio dokaz teoreme.
Implikacija je logicki veznika, a ne "osobina" ili teorema, i ne dokazuje se nego je osnovni simbol u formalnom jeziku, teoriji, a skup osnovnih simbola se zadaje nabrajanjem. Otklonjivost je definisana na sledeci nacin: novouvedeni termin mora biti otklonjiv iz svakog iskaza ili formule teorije u kojoj se pojavljuje; nekreativnost: definicijom ne sme se dobiti tvrdjenje koje se bez nje ne bi moglo dobiti. Dakle nije rec o bilo kakvoj proizvoljnosti, pridavanju bilo kakvih, pa i vrednosnih ocena. Definicija koju sam naveo je jedna od definicija koju Frege koristi u tekstu O smislu i nominatumu, jednom od osnovnih tekstova za proucavanje teorije znacenja, discipline koja se smatra bliskom ili jednim od delova logike. Ali ako ti kazes da je trivijalna... Ne znam zasto si siguran toliko da se sve moze nauciti kroz primere, imao sam na fakultetu kurs iz metodologije, a i citao, slusao sam predavanja iz metodike nastave i pedagogije i nigde nisam nasao takvu eksplicitnu tvrdnju da se sve moze nauciti kroz primere, naprotiv. Ako pogledas ponovo citat, poslednji koji si me citirao, videces da i sam ne mislim da treba sve bubati, ali takodje ne vidim drugi nacin da se nauci, recimo, tablica mnozenja. [ Nedeljko @ 07.03.2009. 20:39 ] @
@Cabo
Očigledno ne razumeš fundamentalne matematičke koncepte. U Vujoševićevom udžbeniku se ta formula dokazuje u formalnom sistemu, gde implikacija nije definisana preko tablica, a tablice su kudikamo starije od tog formalnog sistema i pravljene su prema tablicama, tj. tako da skup teorema bude jednak skupu tautologija definisanom preko tablica. Da, u formalnim sistemima imaš na raspolaganju samo aksiome i pravila izvođenja i nikakve tablice. Matematičke logika je odavno prevazišla svoju početnu svrhu formalnog zasnivanja matematike. Danas se metode matematičke logike koriste u rešavanju problema koji pripadaju ostatku matematike. Jedan od starjiih primera je deseti Hilbertov problem, koji je čisto algebarski, a koji je prvi put rešen metodama matematičke logike (korišćenjem modelske potpunosti teorije realno zatvorenih polja). [ Nedeljko @ 07.03.2009. 20:54 ] @
Citat: Cabo: Može, i upravo je učenje preko primera pravi način da se bilo šta stvarno nauči. To se radi iz Metodike,Pedagogije... Slabo primenljivo na teoriju relativnosti, kvantnu mehaniku, neeuklidske geometrije i neklasične logike. Tamo stečene predstave samo smetaju, pa je formalan pristup neophodan. [ Cabo @ 08.03.2009. 18:31 ] @
Zahvalan sam h4su-u i cozi-ju (njegov prvi odgovor) na jedinim korisnim odgovorima.
Bilo mi je potrebno objašnjenje kako može iz netačnog da sledi tačno. To nisam mogao da shvatim, jer se tome protivi „zdrav razum“. Zahvaljujući njihovim primerima, zatim onom koji sam sam konstruisao, a najzad i dokazu teoreme iz knjige g. Vujoševića, sada mi je to malo jasnije. Svi ostali komentari su potpuno suvišni. [Ovu poruku je menjao Cabo dana 08.03.2009. u 19:49 GMT+1] [ Nedeljko @ 09.03.2009. 10:35 ] @
Opet nisi razumeo sučtinu. Smisao tablice implikacije nije da iz netačnog iskaza može da sledi tačan sikaz, već da iz netačnog iskaza uvek sledi svaki iskaz, pa i onaj koji je tačan.
[ h4su @ 09.03.2009. 13:34 ] @
To je valjda jasno, ali covjek je pitao kako to moze, da vidi na primjeru
[ Nedeljko @ 09.03.2009. 13:46 ] @
Mislim da Cabo-u mnogo toga nije jasno, ali ako ne želi da nauči, nego tera inat, to je njegova stvar.
Suština klasične implikacije je da iz iskaza "konj je ptica" sledi da je Mars planeta. Ako se prihvati drugo shvatanje implikacije, zasnovano na mogućnosti izvođenja jednog iskaza iz drugog (uz bitno korišćenje pretpostavke), onda dobijamo drugi veznik, a to je relevantna imlikacija, kod koje u opštem slučaju formula A=>(B=>A) niej teorema. Dakle, ovo što si naveo je primer slučaja kada su i klasična i relevantna implikacija zadovoljene, premisa je netačna, a konsekvens tačan. No, to nije bilo pitanje iz prvog posta. [ h4su @ 09.03.2009. 14:08 ] @
Dobro da zakljucimo onda ovako ako ne grijesim, kod iskaza p implicira q, q moze a i ne mora imati veze sa p pa odatle je vise nego ocigledno da q moze biti i tacan i netacan iskaz, da ostavimo sad po strani kad je tacan iskaz p implicira q.
[ marinowski @ 09.03.2009. 14:43 ] @
Igorisaću sve što je rečeno, baziraću se samo na početnom pitanju.
Sećam se prvih časova matematike u devetom razredu (mi smo bili poslednja generadija 9. i 10. razreda, tzv. Šuvarova škola), profesorica pita: da li neko ima primer za implikaciju? Ja se javim i kažem: ako pada kiša, ulice su mokre: ako pada kiša, ulice su mokre -> tačno ako pada kiša, ulice nisu mokre -> netačno ako ne pada kiša, ulice su mokre -> tačno (moguće da je neko zalivao, ili je kiša padala ranije) ako ne pada kiša, ulice nisu mokre -> tačno. Još jedan primer koji sam naveo je bio: ako učim onda znam. Zaključak izvedite sami. Ovo su samo tzv. primeri iz svakodnevnog života, nije to najbitnije, bitnije je šta nam implikacija donosi. [ zzzz @ 09.03.2009. 16:07 ] @
Cabo:
Spremam Logiku, pa me interesuje kako se pravda to da pri implikaciji iz netačnog može da sledi tačno: Ništa ne objašnjavam već pokušavam pitati sam sebe, a i ostale, kako bih razumio smisao ovog pojma. 1)Šta znači zapravo ova riječ? -Implikacirati znači obuhvatati, sadržavati u sebi.Riječ potiče iz latinskog jezika. 2)Zašto je je ovaj simbol (relacija, logički veznik između uzroka i posljedice) uveden kao standardni? -Da bi na kraći način opisali neke logičke iskaze, matematičkim jezikom. 3)Da li se svi iskazi koje opisujemo ovom relacijom mogu opisati bez nje, koristeći neke druge relacije? Da, na složeniji način, ali je ponekad teško(?).(Ne, osim verbalno (?).) 4)Može li neko navesti neke primjere logičkih iskaza opisanihi implikacijom i bez nje tj. korištenjem više drugih relacija, (ili verbalno ako ne ide drukčije). -a)... -b)... -c)... ----------- (za mene bi poznavanje ovog bio polazni temelj za uočavanje mjesta upotrebe simbola implikacije sa zadovoljavajućim stepenom sigurnosti.) [ cozi @ 09.03.2009. 19:53 ] @
Implikacija je veznik; relacija je nesto drugo, pojam vezan za skupove i predikatsku logiku...
1,2 ne znam, tj. cini mi se da pitas i odgovaras "iz zivota". 3,4 : Koliko je meni poznato, u iskaznoj logici je moguce (a u predikatskoj ne) s obzirom na funkcionalnu potpunopst iskazne logike, tj. postoje baze veznika, funkcionalno potpun skup veznika koji ne sadrzi implikaciju. Recimo { ¬, V} je funkcionalno potpun skup veznika (postoje i drugi koji ne sadrze implikaciju) : (A->B) <-> ¬AvB Sto ce reci: Ako pada kisa onda su ulice mokre, je logicko ekvivalento, (ili)Ne pada kisa ili su ulice mokre. ili malo slozenija formula... (A->B)->B <-> AvB ako( (vazi) ako pada kisa onda su ulice mokre )onda su ulice mokre , je logicki ekvivalentno, (ili) pada kisa ili su ulice mokre. [ Nedeljko @ 11.03.2009. 10:53 ] @
Citat: marinowski: Igorisaću sve što je rečeno, baziraću se samo na početnom pitanju. Sećam se prvih časova matematike u devetom razredu (mi smo bili poslednja generadija 9. i 10. razreda, tzv. Šuvarova škola), profesorica pita: da li neko ima primer za implikaciju? Ja se javim i kažem: ako pada kiša, ulice su mokre: ako pada kiša, ulice su mokre -> tačno ako pada kiša, ulice nisu mokre -> netačno ako ne pada kiša, ulice su mokre -> tačno (moguće da je neko zalivao, ili je kiša padala ranije) ako ne pada kiša, ulice nisu mokre -> tačno. Još jedan primer koji sam naveo je bio: ako učim onda znam. Zaključak izvedite sami. Ovo su samo tzv. primeri iz svakodnevnog života, nije to najbitnije, bitnije je šta nam implikacija donosi. Za odredjivanje istinitosnih vrednosti ovih iskaza je neophodno znati da li kiša pada i da li su ulice mokre. Ono što je svakako isključeno je da ulice mgu biti suve onda kada pada kiša i sve ostalo ću reći na osnovu . Tako da je iskaz "ako pada kiša, ulice su mokre" uvek tačan. Sa druge strane, iskaz "ako pada kiša, ulice nisu mokre" je netačan ako kiša pada (jer su onda ulice svakako mokre), a tačan u suprotnom. Iskaz "ako ne pada kiša, ulice su mokre" je netačan ako su ulice suve (jer onda svakako ne pada kiša), a tačan u suprotnom. Iskaz "ako ne pada kiša, ulice nisu mokre" je netačan ako kiša ne pada, a ulice su ipak mokre (iz nekog drugog razloga), a tačan u suprotnom. [ zzzz @ 11.03.2009. 23:15 ] @
Ima li još neki primjer osim kiše i mokre ulice?Naprimjer neka padaju
pečene kokoši, a ljudi dole su siti pa neće da ih jedu.Kako bi to išlo? [ holononi @ 13.04.2009. 12:45 ] @
Ne znam kako sa kokoškama ali u jednoj knjizi sam pronašao dokaz da je
(A U B)' = A' ∩ B' U dokazu se koriste De Morganovi zakoni. Ali u knjizi nema dokaza De Morganovih zakona! Šta sad ? [ Nedeljko @ 13.04.2009. 13:22 ] @
Pa, ovo jeste jedan od De Morganovih zakona za skupove. Ako si mislio na De Morganove zakone za iskaznu logiku, oni su tautologije. Možda autor pretpostavlja da čitalac to zna. Recimo, dokazivanje tautologija može biti ranije obrađeno.
[ holononi @ 13.04.2009. 15:05 ] @
Citat: Možda autor pretpostavlja da čitalac to zna. Recimo, dokazivanje tautologija može biti ranije obrađeno. Proverio sam u nekim srednješkolskim udžbenicima. Ni tamo nema dokaza De Morganovih zakona. Koliko znam u matematici se samo aksiome ne dokazuju. (A U B)' = A' ∩ B' Kako dokazati bez De Morganovih zakona ? [ Nedeljko @ 13.04.2009. 15:12 ] @
Matematika se ne mora izlagati aksiomatski. Štaviše, u školama se i ne radi tako.
U gimnazijskim knjigama se obrađuju tautologije, pa samim tim i De Morganovi zakoni kao specijalan slučaj, bez obzira da li se pominju ili ne. [ holononi @ 13.04.2009. 16:23 ] @
Citat: gimnazijskim knjigama se obrađuju tautologije, pa samim tim i De Morganovi zakoni Da, ali nema dokaza ni u knjizi za I ni u knjizi za IV razred gde se navode. Koliko se ja razumem, De Morganovi zakoni nisu aksiome, pa valjda negde treba učenicima dati dokaz. I dalje čekam (A U B)' = A' ∩ B' bez De Morganovih zakona ? [ Nedeljko @ 14.04.2009. 09:19 ] @
U knjizi ti je dat ti je metod za dokazivanje tautologija. Ako ne umeš da dokažeš De Morganove zakone, onda nisi razumeo deo o dokazivanju tautologija. Niko ne može da ti raspiše svih beskonačno mnogo tautologija, ali ti može dati opšti algoritam za ispitivanje da li je data iskazna formula tautologija. Nije poenta u tome da đak nabubeca konačno mnogo tautologija iz knjige, već da nauči opšti slučaj.
[ zzzz @ 14.04.2009. 10:45 ] @
I dalje čekam
(A U B)' = A' ∩ B' bez De Morganovih zakona ? Ako su kao aksiomi data dva operatora ("NE" i naprimjer "I") onda su svi ostali operatori izvedivi iz njih.Dakle samo izvođenje, korištenjem samo datih aksioma, je i dokaz. Evo tog dokaza pomoću geometrijskog prikaza. 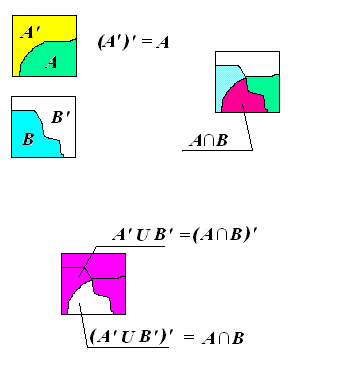 [ holononi @ 14.04.2009. 13:56 ] @
Citat: Evo tog dokaza pomoću geometrijskog prikaza. Veoma lepo i ubedljivo. Mislim da bi se srednješkolcima dosta olakšalo ovakvim skicama. Ali ja sam glupav, hoću DOKAZ a ne da mi se crta ko debilu. [ Nedeljko @ 15.04.2009. 13:54 ] @
Znak jednakosti bi trebalo zameniti znakom ekvivalencije.
[ holononi @ 15.04.2009. 18:31 ] @
Citat: Lokanje u bircuzu @Lokanje u bircuzu Napredujemo, treba krenuti po definicijama i posmatrati proizvoljan element. Problem u tvom dokazu je što se u pretposlednjem koraku pozivaš na De Morganove zakone, a tražen je dokaz bez primene de Morganovih zakona. Ali nemojte se sekirati, ima i univerzitetskih profesora koji bi trebalo a ne bi mogli to da dokažu. [ zzzz @ 15.04.2009. 19:05 ] @
holononi.Ajde probaj sam napraviti analitički dokaz.Evo malo uputa:
-Napraviti sve moguće tablice istine za dvije binarne varijable.Imaš 16 različitih funkcija. -Napraviti isto za jednu varijablu.Ima 4 različite funkcije. Diskusija i izbor minimalnoog broja funkcija pomoću kojih možeš izraziti ostale. [ holononi @ 15.04.2009. 21:17 ] @
Ovi skupovi imaju 67856936459634956634985693465634659636534956439856983659389709798070723239563894563658364563458634563405863450630 elemenata !
Kako da nacrtam toliku tablicu ? [ Nedeljko @ 16.04.2009. 08:08 ] @
Citat: holononi: @Lokanje u bircuzu Napredujemo, treba krenuti po definicijama i posmatrati proizvoljan element. Problem u tvom dokazu je što se u pretposlednjem koraku pozivaš na De Morganove zakone, a tražen je dokaz bez primene de Morganovih zakona. Ali nemojte se sekirati, ima i univerzitetskih profesora koji bi trebalo a ne bi mogli to da dokažu. Šta ti zapravo hoćeš? Ako ne radiš matiš kroz aksiomatsku teoriju skupova, onda se logika podrazumeva. OK, ne mora neko da zna za De Morganove zakone da bi ovo ukapirao, već treba da zna postupak dokazivanja skupovnih identiteta, odnosno postupak dokazivanja tautologija i nikada ne mora da sazna kako se ti zakoni zovu. Ako hoćeš nešto što suštinski ne koristi De Morganove zakone, moraš formulisati neklasičnu logiku u kojoj ti zakoni ne važe, pa posmatrati problem u njoj. Međutim, tamo ni De Morganovi zakoni za skupove neće važiti, jer je to isto. [ Nedeljko @ 16.04.2009. 08:13 ] @
[ holononi @ 16.04.2009. 08:49 ] @
Citat: već treba da zna postupak dokazivanja skupovnih identiteta ... i eto rešenja. [ Nedeljko @ 16.04.2009. 11:11 ] @
[ Cabo @ 16.04.2009. 15:06 ] @
Citat: holononi: @Lokanje u bircuzu To je u odgovor na izraz „Lokacija:“. Što se tiče teme, pridružiću se Nedeljku u pitanju „šta ti zapravo hoćeš?“ Zašto bismo uopšte zanemarivali De Morganove zakone? [ holononi @ 16.04.2009. 16:14 ] @
Citat: Zašto bismo uopšte zanemarivali De Morganove zakone Neću ja ništa da zanemarim. Dokazi mogu da se izvedu na razne načine. A eto, ja zap'o za dokaz bez primene De Morganovih zakona. Šta je tu neobično? [Ovu poruku je menjao holononi dana 16.04.2009. u 17:25 GMT+1] [ Nedeljko @ 16.04.2009. 16:23 ] @
Problem je u formulaciji "izvesti bez ovoga i onoga". Ja uvek mogu za dlaku da promenim De Morganove zakone i dodam nešto iz čega oni odmah slede i da dokažem teoremu preko toga. To je poenta ovoga
Citat: Nedeljko: Pa, onda je ovo što je Cabo napisao OK. Druga je stvar što iskaz "ne koristiti De Morganove zakone" nema previše smisla. Moraš da koristiš ili njih ili nešto iz čega oni slede. Na primer: 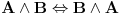 , ,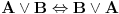 , ,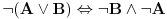 , ,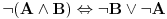 . .[ petarm @ 17.04.2009. 01:40 ] @
Citat: Nedeljko: Slabo primenljivo na teoriju relativnosti, kvantnu mehaniku, neeuklidske geometrije i neklasične logike. Tamo stečene predstave samo smetaju, pa je formalan pristup neophodan. Netacno za teoriju relativnosti i KM. U fizici postoji i nesto sto se zove eksp. I taj eksp. nam daje te predstave! A formalan pristup je ipak u sprezi sa ovim predstavama! [ zzzz @ 17.04.2009. 11:14 ] @
holononi : "Neću ja ništa da zanemarim. Dokazi mogu da se izvedu na razne načine. A eto, ja zap'o za dokaz bez primene De Morganovih zakona. Šta je tu neobično?"
Na donjoj slici su prikazane sve moguće funkcije dviju binarnih varijabli. Među njima uočimo i za nas najinteresantnije funkcije.To su "Ili" funkcija i "I" funkcija.Veza među njima korištenjem još i negacije "Ne" se jednostavno izvodi, i to što je izvedeno je De Morganov zakon.  [ Nedeljko @ 17.04.2009. 11:56 ] @
Citat: petarm: Netacno za teoriju relativnosti i KM. U fizici postoji i nesto sto se zove eksp. I taj eksp. nam daje te predstave! A formalan pristup je ipak u sprezi sa ovim predstavama! Ali izlaganje nije induktivno, već deduktivno. Govorim o pedagoškom pristupu. Eksperimenti su OK, kao i njihov formalan opis. Onaj pristup izlaganju koji postavljač teme pominje nije primenljiv na TR. Vidi na temi za TR na forumu za fiziku zbog čega. [ holononi @ 17.04.2009. 14:02 ] @
@zzzz
Dobro, dokazuješ De Morgan-ove zakone. Apsoluno ne sumnjam u njih. Problem je u sledećem: Definišemo pojmove unije, preseka, razlike i komplementa skupova. Kako sada dokazati da je komplement unije jednak preseku komplemanta datih skupova a da se koriste isključivo uvedene definicije i aksiome neke od teorije skupova? U odgovoru koji je ponudio @Cabo sve funkcioniše do pretposlednjeg koraka. Tada se iz teorije skupova "preskače" u iskazni račun. Naravno, ako su prethodno dokazani De Morganovi zakoni i pokazano da oni važe i na skupovima onda takav postupak i nije problem. Medjutim, u srednješkolskim knjigama to nije eksplicitno učinjeno. Zato sam pokrenuo pitanje kako izvesti dokaz bez primene De Morganovih zakona. Problem je kako taj pretposlednji korak zadržati u okviru teorije skupova? Odgovor je sadržan u rešenju koje je ponudio @zzzz u svom postu od 14.04.2009. Samo što to sada treba matematički formalizovati. [ Nedeljko @ 18.04.2009. 11:01 ] @
[ holononi @ 18.04.2009. 12:49 ] @
@Nedeljko
Ovo je u redu. Takav je otprilike redosled izlaganja na fakultetima. Prvo iskazni račun, zatim predikatski račun i tek potom teorija skupova. Ako idemo tim redom onda imamo rešenje. Medjutim, kako sam problem postavio u kontekst srednje škole gde takav redosled nije ispoštovan problem se javlja u tome što se De Morganovi zakoni za uniju odnosno presek skupova daju a da učenik nije prethodno usvoji osnovne stavove iskaznog i predikatskog računa (govorim o formalnom vidjenju a realno učenik možda ima znanja koja daleko prevazilaze traženo). Zatim se u "dokazima" De Morganovih zakona za skupove jednostavno "preskoči" na De Morganove zakone u iskaznom računu i to je "dokaz" a da nigde nije uspostavljena ekvaivalencija takvih dokaza. Jedan način rešenja ovog problema je jednostavno u tome da se obrazlži svaki korak Ω - univerzalan skup, A podskup Ω, B podskup Ω. A U B = {x: x ε A ili x ε B} A ∩ B = {x: x ε A i x ε B} A \ B = {x: x ε A i x ¬ε B} A' = {x: x ε Ω i x ¬ε A} Dokazati (A ∩ B)' = A' U B' (1) x ε (A ∩ B)' ≈ (koristimo definiciju komplementa) (2) x ε (Ω \ (A ∩ B)) ≈ (definicija razlike) (3) (x ε Ω) i (x ¬ε (A ∩ B)) ≈ (kako se x ne nalazi u preseku skupova tada nije bar u jednom od njih) Tako da ovde učenik ostaje fokusiran na skupove i ne mora ni da je čuo za De Morganove zakone (4) (x ε Ω) i ((x ¬ε A) ili (x ¬ε B)) ≈ (distributivnost) (5) ((x ε Ω) i (x ¬ε A)) ili ((x ε Ω) i (x ¬ε B)) ≈ (razlika skupova) (6) (x ε (Ω \ A)) ili (x ε (Ω \ B)) ≈ (a ovo je komplement) (7) (x ε A') ili (x ε B') ≈ (definicija unije) (8) x ε (A' U B') [ Cabo @ 18.04.2009. 16:38 ] @
Jedno pitanje: zašto srednjoškolci (svi osim onih iz Matematičke gimnazije, za njih je to donekle razumljivo) moraju da dokazuju tvrđenja?
[ holononi @ 18.04.2009. 17:47 ] @
U knjizi za I razred srednje škole (i opšteg smera gimnazije) broj teorema po glavama
1. Logika i skupovi 5 2. Relani brojevi 7 3. Proporcionalnost 1 4. Uvod u geometriju 12 5. Podudarnost 69 (da 69) 6. Racionalni algebarski izrazi 11 7. Homotetija i sličnost 15 8. Trigonometrija pravouglog trougla 1 Ukupno 121 teorema! No coment. [ Nedeljko @ 18.04.2009. 18:34 ] @
U teoriji skupova ne postoji pojam univerzalnog skupa, jer taj pojam vodi u protivrečnost. Komplement skupa se uvek posmatra u odnosu na neki fiksiran nadskup.
Problem u školama sa iskaznim računom je što niko ne kaže čemu to služi i nigde se ne primenjuje. Suština je da je svaka instanca tautologije tačno tvrđenje i onda nema problema sa Cabo-vim dokazom. Đaci treba da dokazuju tvrđenja, jer na taj način vežbaju rezonovanje. Rezonovanje im je neophodno, kako za izradu zadataka, tako i za kasniju primenu znanja, jer će retko realan problem da ima tačnu formulaciju nekog stava, već je potrebno nešto povezati. [ holononi @ 18.04.2009. 20:51 ] @
Citat: Suština je da je svaka instanca tautologije tačno tvrđenje i onda nema problema sa Cabo-vim dokazom. Ima jer djaci u prvom tromesečju prvog razreda nisu stekli znanja o tautologijama, iskaznom računu, predikatskom računu (osim što su možda čuli za takav "staf"). Bez odgovarajućeg predznanja njihovi "dokazi" su samo puko rendiranje simbola u tekstualne nizove nalik onima koje je nastavnik ispisao na tabli. Djaci će na kraju tromesečja dobiti ocene koje će uticati na njihov konačan uspeh, pa i život a da im nikad nije data prava i fer prilika. Jer koliko vidima, brz si na obaraču pa ćeš odmah skočiti (a i ja bih reagovao) kad bi neko pokušao da dokaže De Morganove zakone pomoću de Morganovih zakona. Citat: U teoriji skupova ne postoji pojam univerzalnog skupa, jer taj pojam vodi u protivrečnost. Potpuno si u pravu ako misliš na "skup svih skupova". Medjutim univerzalni skup koji uvodim nije tako definisan. Pažljivo pročitaj pa ćeš videti da Ω nije "skup svih skupova" inače da jeste ne bih morao da navodim da su A i B podskupovi Ω. [ Cabo @ 22.04.2009. 14:45 ] @
Citat: Nedeljko: Đaci treba da dokazuju tvrđenja, jer na taj način vežbaju rezonovanje. Rezonovanje im je neophodno, kako za izradu zadataka, tako i za kasniju primenu znanja, jer će retko realan problem da ima tačnu formulaciju nekog stava, već je potrebno nešto povezati. Ja ne smatram da je izvodivo, a ni potrebno, opterećivati ionako preteško gradivo matematike potrebom dokazivanja stavova. To ni od moje generacije gimnazijalaca nije traženo, već su profesori radili mimo nakaradnog programa. Iz sadašnje perspektive mi se diže kosa na glavi kada vidim da se taj „srednjoškolski“ program u sitnim stvarima razlikuje od fakultetskog programa, recimo Analize I. To se u tekućim reformama mora menjati i pojednostaviti! Javna je tajna da je sadašnje stanje takvo da profesori u srednjim školama ili masovno dele „kečeve“ ili odstupaju od programa, pojednostavljujući gradivo. Po mom uverenju, u „običnim“ srednjim školama i gimnazijama se mora insistirati na primenama, a ne na teoretisanju. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|