[ kingakul @ 05.03.2009. 08:41 ] @
Da li neko zna da resi ovu diferencijalnu jednacinu?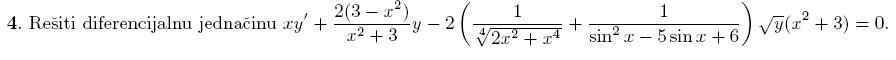 Izvor: http://file.sf.bg.ac.rs/nastav...tike_1/DrugiKolokvijum06M1.pdf |
|
[ kingakul @ 05.03.2009. 08:41 ] @
[ Nedeljko @ 05.03.2009. 10:35 ] @
[ kingakul @ 05.03.2009. 11:41 ] @
OK svodi se na Bernulijevu, ali se dobije integral koji ne moze da se resi (prvi sa iracionalnom funkcijom).
 Zar je moguce da se ovako nesto dogodi na roku iz Matematike 1? [ igorpet @ 05.03.2009. 17:38 ] @
[ kingakul @ 05.03.2009. 23:58 ] @
Svaka cast obojici!
Mislio sam da ne pokusavam da resim kada sam video da Wolframov Integrator izbacuje hipergeometrijsku f-ju. Kako to da ne izbacuje ovakvo resenje preko elementarnih f-ja? [ Nedeljko @ 06.03.2009. 09:38 ] @
Tako lepo što ovaj ispit ne polaže volframov integrator, nego student Saobraćajnog fakulteta, koji je imao nešto slično na vežbama.
[ igorpet @ 06.03.2009. 09:38 ] @
Citat: kingakul: Svaka cast obojici! Mislio sam da ne pokusavam da resim kada sam video da Wolframov Integrator izbacuje hipergeometrijsku f-ju. Kako to da ne izbacuje ovakvo resenje preko elementarnih f-ja? Pa to je problem sa matematickim programima (ili online resavacima), jos nisu dostigli "znanje" jednog malo boljeg matematicara, barem za sada, i ne mozes se u potpunosti osloniti na njih. Imaju oni dosta problema sa integralima, jer prepoznaju samo sablonske tipove integrala i cim u bazi nema tog sablona programi ga ne mogu resiti preko elementarnih f-ja. [ kingakul @ 06.03.2009. 12:19 ] @
Evo u cemu je caka. Kada se unese stepen kao realan broj:
http://integrals.wolfram.com/index.jsp?expr=(1-(x%2B1)^0.5)%2F(1%2B(x%2B1)^(1%2F3))&random=false i kada se unese kao razlomak: http://integrals.wolfram.com/index.jsp?expr=(1-(x%2B1)^(1%2F2))%2F(1%2B(x%2B1)^(1%2F3))&random=false [ Nedeljko @ 06.03.2009. 18:46 ] @
Citat: igorpet: Pa to je problem sa matematickim programima (ili online resavacima), jos nisu dostigli "znanje" jednog malo boljeg matematicara, barem za sada, i ne mozes se u potpunosti osloniti na njih. Imaju oni dosta problema sa integralima, jer prepoznaju samo sablonske tipove integrala i cim u bazi nema tog sablona programi ga ne mogu resiti preko elementarnih f-ja. Mislim da volframov integrator odavno ne radi tako, ali nemoj očekivati da rešenje koje izbaci uvek ima oblik koji si ti hteo. [ igorpet @ 06.03.2009. 19:54 ] @
Citat: Nedeljko: Mislim da volframov integrator odavno ne radi tako, ali nemoj očekivati da rešenje koje izbaci uvek ima oblik koji si ti hteo. Ja mislim suprotno, tj. da svi matematicki programi (ili skoro svi) npr. integrale resavaju na osnovu predefinisanih sablona sa minimalnim koriscenjem vestacke ineligencije. Mislim da programi do resenja dolaze algoritmima koji su potpuno drugaciji od nacina na koji mi resavamo zadatke, i da je glavi deo u progamu u stvari parsiranje unesenog teksta (zadatka) i da nakon toga ide trazenje resenja u bazu, i ako u bazi nadje odgovarajuci tip (mislim da ovde koriste nesto od "pametnih" algoritama za prepoznavanje) prikaze se resenje u onom obliku kako je navedeno u bazi. (i ne zaboravimo cinjenicu da je npr. samo opticko prepoznavanje teksta na racunaru pravi programski izazov i da tek od skora postoje odgovarajuci algoritmi sa zadovoljavajucim procentom uspesno prepoznatih karaktera). Ovo iznosim jer sam pre 1-2 god. radio na pitanju kreiranja (programiranja) elektronskih zbirki zadataka koje bi imala detaljna resenja. Uspeo sam da relativno elegantno odradim prikaz poznatog resenja ali je malo veci izazov bio da korisnik sam definise zadatak i da program prikaze postupak resenja. Naravno, ja sam daleko i po mogucnostima i po znanju iza velikih programerskih kuca koji se bave ovim pitanjima, ali pokusao sam da pronadjem neka gotova resenja pa da ih malo proucim, ali nisam uspeo da pronadjem nesto tako (sem jednog izuzetka). Svi matematicki programi su izbacivali samo resenje a ne i postupak (ili barem neki od medjukoraka). Zato mislim da oni koriste nesto poput ovoga:  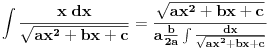 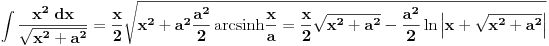 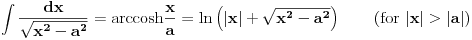  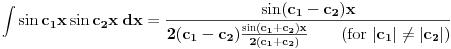 i resenja su onakva kakva su data u bazi, i zato se ne mogu korigovati. Ako bi koristili neki drugi princip, mislim da bi mogli da prikazu neki medjukorak u resavanju. I mislim da online Volframov integrator sluzi i da pomogne ali i da skuplja zadatke cijih resenja nema u bazi i verujem da neresene tipove analizira i resava tim ljudi i ubacije u naredne verzije programa i zato su programi ovog tipa sve bolji i bolji, ali u smislu povecanje baze a ne i u sistemskom pristupu resavanja problema. Naravno, ne tvrdim da je to bas ovako kako navodim, ali moja saznanja su ovakva. I otiso sam malo u offfff, ali cisto da malo pojasnim zasto se ne mozema bas uvek pouzdati u programe. [ Nedeljko @ 06.03.2009. 20:32 ] @
Ček, polako. Niz predefinisanih pravila shvatam kao algoritam, a to je jedini način na koji računar može da radi. Veštačka inteligencija se takođe zasniva na nekim algoritmima.
Ja sam mislio da ti misliš da računar prepoznaje konačan broj tipova integrala (racionalne funkcije trigonometrijskih itd.), ali svakako da računar ne rešava te integrale metodama kojima se mi služimo, već koristi opštije algoritme, kojima možeš da ubaciš praktično bilo koji izraz na određenom jeziku i da dobiješ nekakav rezultat. Da, skup elementarnih funkcija nije zatvoren za operator integracije, ali neki širi skupovi jesu. Koriste se one teorije pomoću kojih se inače dokazuje da integrali nekih elementarnih funkcija nisu elementarne funkcije. [ igorpet @ 06.03.2009. 21:34 ] @
Samo sam hteo da kazem da ne postoje (barem koliko sam ja uspeo da saznam) toliko sofisticirani programski algoritmi koji bi uspeli da rese svaki integral preko elementarnih f-ja iako takvo resenje postoji i ne mogu da prikazu postupak resavanja zato sto oni i nemaju postupak resavanja jer zadatak uporedjuju sa raspolozivom bazom i resenje daju na osnovu sablona datih u bazi (kao neka tabelarna resenja koja sam naveo u prethodnoj poruci).
I mislim da računar prepoznaje konačan broj tipova (podtipova) integrala (naravno uz pravilno prepoznavanje koeficijenata uz nepoznate). [ Bojan Basic @ 06.03.2009. 22:11 ] @
Samo bih napomenuo da postoji softver koji može proceniti da li se integral zadate funkcije može prikazati preko elementarnih funkcija. Ipak, on nije kompletan, u smislu da za neke funkcije jednostavno nije u stanju da proceni izrazivost integrala preko elementarnih funkcija — ali, naravno, ukoliko izbaci negativan odgovor na to pitanje, onda odgovor i jeste negativan (ukoliko u samom programu ne postoji greška). Zove se Axiom, i možda će nekom koristiti (čak je i besplatan).
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|