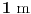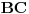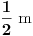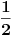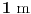
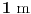
Prvi potcilj je da napravimo trougaonu mrežu od tačke do neke tačke blizu tački (blizu znači manje od ). Ovo nije teško uraditi: opišemo kružnice i poluprečnika (ili manje, nije bitno, samo da fiksiramo jednu vrednost) oko tačaka i , redom. Zatim odaberemo proizvoljnu tačku na kružnici i, počev od nje, nađemo još pet tačaka koje s uočenom čine temena pravilnog šestougla upisanog u . 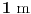Onda crtamo kružnice poluprečnika s centrom u svakoj od ovih novih tačaka, pa opet šestouglove tako što će polazno teme sada biti tačka , i tako se širimo sve dok ne dobijemo presek s kružnicom . Neka je taj presek tačka , i neka je sredina duži (ovo možemo naći, jer je sve u dometu lenjira i šestara). Dalje, povucimo izlomljenu liniju od tačke do tačke (jasno, po nacrtanoj mreži). Sada nam je potcilj da iz tačke nacrtamo izlomljenu liniju čije je svako parče paralelno odgovarajućem parčetu izlomljene linije od do (tj. idemo „unatrag“), i dva puta kraće od njega. 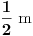Jasno, ta izlomljena linija ne mora ići po iscrtanoj mreži, mada hoće po drugoj, dva puta finijoj, a liniju crtamo na sledeći način: oko tačke opišemo kružnicu poluprečnika (tj. polovina maločas fiksirane vrednosti), povučemo kroz tačku pravu paralelnu prvom parčetu izlomljene linije od do , i u preseku te prave s upravo nacrtanom kružnicom (izbor preseka je uslovljen smerom koji nam treba) dobijamo tačku od koje ćemo dalje praviti šestouglove. Za naredne parčiće izlomljene linije koju konstruišemo nije nam potrebna konstrukcija paralelnosti (srećom, jer tu slobodu više ne bismo imali), već samo pratimo „poteze“ s linije koju preslikavamo. Konačno, neka je kraj ove izlomljene linije tačka . No, primetimo da su, po konstrukciji, dve izlomljene linije s kojima smo radili homotetične iz tačke , s koeficijentom homotetije ! 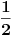Drugim rečima, tačka je sredina duži , čime je zadatak rešen: dovoljno je polovljenjem (koje izvodimo na opisan način) naći na duži dovoljno tačaka blizu jednih drugima, i pospajati ih lenjirom.

Hvala.