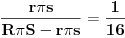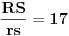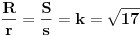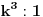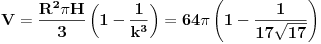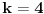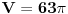[ serpikons @ 27.03.2009. 15:02 ] @
| Molim za pomoc za resavanje sledeceg zadatka: Kupa visine 12 i poluprecnika osnove 4 presecena je sa ravni paralelnoj osnovi. Time je omotac kupe podeljen na dva dela cije se povrsine odnose kao 1:16. Izracunati zapreminu tako nastale zarubljene kupe. Hvala najlepse! |