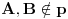[ sabandijilla @ 29.03.2009. 12:53 ] @
|
[ galet@world @ 30.03.2009. 09:27 ] @
Možda bi ovo moglo biti rešenje.
Nisam napisao komentar, ali ako treba napisaću. Samo da kažem da je kružnica k bilo koja kružnica koja ima centar na simetrali tetive AB i da dodiruje pravu p. Ostalo je vidljivo sa slike. [ galet@world @ 31.03.2009. 12:10 ] @
Data je prava p i normala na tu pravu. Negde na normali se nalazi tačka A.
Treba naći položaj tačke B koja je jednako udaljena od tačke A i od prave p [ Farenhajt @ 31.03.2009. 12:25 ] @
Citat: galet@world: Data je prava p i normala na tu pravu. Negde na normali se nalazi tačka A. Treba naći položaj tačke B koja je jednako udaljena od tačke A i od prave p Pa, počnimo od središta duži između tačke A i podnožja normale... A završimo parabolom čija je žiža A, a izvodnica prava p. Međutim, koliko znam, parabola se ne može konstruisati šestarom i lenjirom. [ galet@world @ 31.03.2009. 12:53 ] @
Citat: Farenhajt: ...Međutim, koliko znam, parabola se ne može konstruisati šestarom i lenjirom. Ne moraš da konstruišeš parabolu. Nema potrebe. Uzmi najjednostavniji slučaj i konstruiši kvadrat sa stranicom koja ima dužinu koliko je rastojanje od tačke A do preseka normale sa pravom p Tačka B je na uglu kvadrata koji je dijagonalno naspram tog preseka, ali to je specijalan slučaj - treba naći tačku B u opštem slučaju. [ Goran Milovanovic @ 31.03.2009. 13:08 ] @
Farenhajt je i dao resenje u opstem slucaju. Jedino sto je malo
terminoloski neprecizan. Naime, prava p je direktrisa (vodilja). Ako posmatramo zadatak u 3D onda bi navedenu parabolu mogli smatrati izvodnicom (generatrisom) povrsi cije sve tacke zadovoljavaju uslove zadatka. [ galet@world @ 31.03.2009. 14:26 ] @
Sve je to što kažeš sasvim u redu, ali ostaje i dalje pitanje kako konstruisati neku - bilo koju tačku koja zadovoljava postavljeni uslov - naravno to se može uraditi vrlo jednostavno pomoću lenjira i šestara. Dakle, ako je pomoću lenjira i šestara moguće konstruisati bilo koju tačku parabole ostaje pitanje: da li u tom slučaju možemo reći da parabolu možemo ili ne možemo konstruisati kao što kaže Farenhajt, jer u principu je on možda u pravu jer ne možemo konstruisati kontinualnu parabolu kao što možemo, na primer, kružnicu. [ Farenhajt @ 31.03.2009. 14:58 ] @
Izvinjavam se na terminološkom propustu (davno je bilo...)
Galet, parabola je geometrijsko mesto s neprebrojivo mnogo tačaka, te je svakako ne možeš konstruisati "tačku po tačku" (što bi bio prebrojiv, mada takođe beskonačan postupak) šestarom i lenjirom. A u konstruktivnim zadacima, kad se kaže "konstruisati tačku", uvek se misli na "konstruisati geometrijsko mesto SVIH tačaka koje zadovoljavaju uslove konstrukcije". Uzgred, Gorane, u 3D bi se dobio paraboloid - kakvog tipa? Ne izgleda mi kao rotacioni. [ Goran Milovanovic @ 31.03.2009. 16:37 ] @
Kada bi se posmatrala ravan umesto prave p, bio bi rotacioni, a ovako, verovatno neki hiperbolicki.
[ galet@world @ 31.03.2009. 19:52 ] @
Zadatak je jednostavan i rešen u principu, ali može da se ulepša. (Ako neko želi) Kako konstruisati neku tačku parabole lenjirom i šestarom, ako nije dozvoljeno da se konstruišu i koriste linije paralelne sa pravom p. [ Farenhajt @ 01.04.2009. 04:47 ] @
Citat: galet@world: Zadatak je jednostavan i rešen u principu, ali može da se ulepša. (Ako neko želi) Kako konstruisati neku tačku parabole lenjirom i šestarom, ako nije dozvoljeno da se konstruišu i koriste linije paralelne sa pravom p. Ni to nije neki problem. Odabereš proizvoljnu tačku 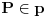 , a onda konstruišeš pravu , a onda konstruišeš pravu  takvu da je takvu da je 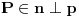 . Tražena tačka . Tražena tačka  biće presek prave biće presek prave  i simetrale duži i simetrale duži 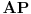 (gde je (gde je  data žiža). data žiža).[ galet@world @ 01.04.2009. 14:23 ] @
Citat: Farenhajt: Ni to nije neki problem. Odlično! Rešio si nivo 2 ili level 2. Pređimo na level 3. Sledeće ograničenje je da se ne sme konstruisati niti koristiti nikakva dodatna normala na pravu p Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|