Ti svake godine sve ranije počinješ s pripremama za takmičenje, bar ako sudimo po tvojim porukama na ovom forumu.

Označimo sa navedenu sumu izvoda, i neka je . Uočimo da tada važi . Dakle, funkcija je opadajuća, a iz dobijamo da je sve vreme pozitivna. Jasno, i znak funkcije je isti.

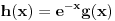
Hvala! Ova fora sa je baš dobra. Uz pomoć toga, sad sam ga riješio na još tri načina. Neće mene jedan zadatak zafrkavati Hvala još jednom.

A sa pripremama počinjem ranije, jer za ranije pomjeraju i takmičenja. A ovo mi je i zadnja prilika da ugrabim neku medalju. Ovdje je pravo rasulo što se tiče takmičenja. Ispitnom centru (ustanova koja je dosad organizovala takmičenja) je ove godine dunulo da organizuje takmičenja samo za 3. razrede srednje škole. Posle toga je Društvo matematičara i fizičara odlučilo da organizuje posebno takm. za sve razrede. I sad jedni učenici idu na jedno, drugi na drugo, neki na oba (ali se "slučajno" desilo da se oba takmičenja održavaju u isti dan), i na osnovu kojeg će se formirati ekipa za BMO i IMO, niko pojma nema...