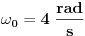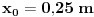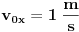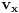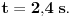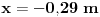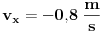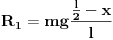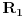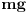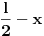[ R A V E N @ 03.04.2009. 09:36 ] @
|
[ zzzz @ 03.04.2009. 11:08 ] @
Oscilovanje duž x ose možeš posmatrati i kao rotaciju kuglice u x-y ravni
oko z ose, i umjesto da posmatraš kretanje sa nivoa ravni gledaj to odozgo. -Napraviti skicu i unijeti date vrijednosti. Pa sad možeš iz projekcije obodne brzine, kao i projekcije radijusa rotacije (amplituda) napraviti dvije jednačine.Iz njih izračunaš radijus i taj trenutni ugao.(Ovdje treba pripaziti kako je usmjerena komponenta obodne brzine).Sad je lako dalje nastaviti rotaciju i naći ugao nakon 2.4 s. [ R A V E N @ 03.04.2009. 15:26 ] @
Pogledati ću to malo kasnije.Sada imam jedno pitanje koje me zbunjuje:
U dvije različite knjige našao sam dva različita izraza za položaj tačke pri oscilacijama koji se razlikuju samo u funkciji koja je korištena - jednom sinus a drugi put kosinus: 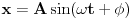 i i 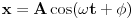 . .Nagađam da je ovaj sa sinusom glavni izraz,a ovaj sa kosinusom njegova specijani slučaj koji se dobiva kada se faza pomjeri za 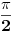 unaprijed.Zašto se to radi? unaprijed.Zašto se to radi?Slično imamo i kod talasa: 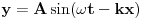 i i 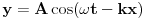 . .[ Milan Milosevic @ 03.04.2009. 21:13 ] @
Zavisi od slucaja do slucaja. Pod normalnim okolnostima se uzima sinusna funkcija jer daje resenje nula za t=0, kada nema pocetne fazi i maksimalnu brzinu posle cestice koja prolazi kroz ravnotezni polozaj.
Zadatak cinimi se se resava tako sto postavis sistem jednacina xo=AsinWt vo=ACosWt odavde nades ampitudu, a eliminises vreme i zamenis posle za dato vreme u te dve jednacine t dobijenu ampiltudu A. Zadnje dve jednacine ti se odnose na ravne talase. [Ovu poruku je menjao Milan Milosevic dana 03.04.2009. u 22:24 GMT+1] [ zzzz @ 03.04.2009. 22:34 ] @
U dvije različite knjige našao sam dva različita izraza za položaj tačke pri oscilacijama koji se razlikuju samo u funkciji koja je korištena - jednom sinus a drugi put kosinus:
To ovisi od izbora koordinatnog sistema.U matematici je po konvenciji pozitivan prirast ugla suprotan kretanju kazaljke na satu, a počinje od poz smjera x ose. U mehanici se često smjer kazaljke na satu označava kao pozitivan, a ugao počinje od y ose. Može se koristiti i jedno i drugo samo treba skicom naznačiti šta je odabrano. 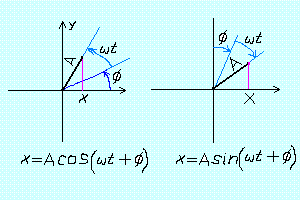 [ R A V E N @ 05.04.2009. 19:41 ] @
Hvala.To mi nisu znali reći ni na američkom forumu...ili im se nije dalo.
Što se tiče druga dva od preostala tri zadatka,njih nisam htio da postavim dok ne iscrpim svoje moći,ali ih je,by lucky strike,već neko drugi postavio na Opruge i oscilovanje (hitno mi treba).Čak su i priložene slike identične onima u mojoj knjizi,koju očigledno koriste negdje i u Sarajevu(samo što mi imamo predavanja ponedeljkom kada i predajemo zadaće i dobivamo tri umjesto pet zadataka).Prilično sam siguran da kod nas ovo skoro niko ne zna riješiti potpuno samostalno,tj. da ne pita makar nekoga za sugestiju ili uputu ili već se konsultuje sa riješenim primjerom koji tretira sličan ili identičan problem. Prilično sumnjam da je korisnik07 dosada riješavao zadaće samostalno ako je u pitanju ta ista knjiga,osim možda nekih zadataka iz molekularno-kinetičke teorije i tu i tamo koji iz translatorne i rotacione kinematike. Treći zadatak je poseban slučaj prvog,samo sada tijelo visi,jednom na dvije serijski vezane opruge,a drugi put opruge su vezane paralelno. Ja sam mislio da sam tačno riješio prvi zadatak sa odgovorom da su periodi oscilovanja jednaki,jer su smjerovi sila u oba slučaja isti,pa ako se u oba slučaja tijelo otkloni za  ,sile se,odnosno koeficijenti ,sile se,odnosno koeficijenti  jednostavno saberu. jednostavno saberu.Interesuje me samo da li ste se već susreli u toku školovanja/rada sa ovakvim specijaliziranim slučajevima(paralelne i serijske opruge i daska na valjcima) ili ste ih riješili sada odmah na osnovu opšteg znanja? [Ovu poruku je menjao R A V E N dana 05.04.2009. u 21:26 GMT+1] [ Milan Milosevic @ 05.04.2009. 21:27 ] @
[ R A V E N @ 05.04.2009. 21:33 ] @
Linearne harmonijske oscilacije.
 [ R A V E N @ 05.04.2009. 22:48 ] @
Samo da budem siguran,ovo je identično paralelnoj vezi iz pokazanog zadatka?:
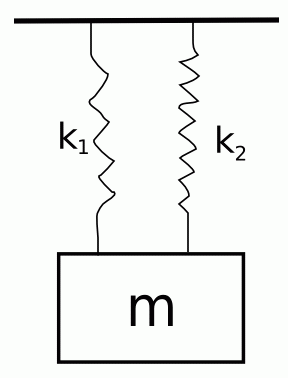 [ zzzz @ 05.04.2009. 22:59 ] @
Da.
Konstanta opruge je omjer sile i progiba pa se ove dvije opruge mogu zamjeniti jednom "jačom" koja ima konstantu jednaku sumi ove dvije. [ R A V E N @ 06.04.2009. 00:22 ] @
[ zzzz @ 06.04.2009. 00:36 ] @
Nije dobro tako razmišljati.
Statika traži da suma sila bude jednaka 0, ali i suma momenata takođe. Zgodnim izborom tačke oko koje računamo momenat eliminišem drugu reakciju i obadvije sile trenja jer su im krakovi 0 i ne prave nikakav momenat. To je tačka dodira na desnom valjku. (Možemo mi odabrati bilo koju tačku, ali u interesu nam je jednostavnost.) Ostaje samo momenat lijeve reakcije i momenat težine grede.Odatle je R1. [ R A V E N @ 06.04.2009. 00:53 ] @
Back to the roots.
To bi bilo to.Hvala još jednom. [ R A V E N @ 06.04.2009. 18:24 ] @
Moram opet da ovo podignem da bih raščistio sa nekim stvarima.
1.)zzzz: Ubrzanje je drugi izvod puta po vremenu pa ispada da je x"=-kx, a to znači da tražimo x=f(t) kojoj je drugi izvod jednak toj funkciji, a suprotnog predznaka. Mi zapravo imamo ovdje 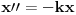 , a ne , a ne 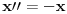 ? ?2.)zzzz: Takav slučaj je kod sin(t) i cos(t) Ovo znamo iz iskustva,dakle to vrijedi samo kod ove dvije funkcije? 3.)zzzz:Ako napraviš prvi i drugi izvod opšteg rješenja i usporediš sa svojim, moći ćeš naći koliko je "omega" i "fi" a onda i T=1/omega. Je li misliš ovako:pošto smo već zaključili da je naša funkcije kosinus(ili sinus),njen opšti oblik je 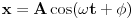 .Uradimo drugi izvod ovog izraza po .Uradimo drugi izvod ovog izraza po  i dobijemo i dobijemo 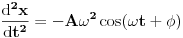 .Ovo izjednačimo s našim izrazom .Ovo izjednačimo s našim izrazom 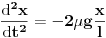 ...slijepa ulica.Kako naći ...slijepa ulica.Kako naći  ? ?[ zzzz @ 06.04.2009. 19:23 ] @
Mi zapravo imamo ovdje x"=-kx
Tako je.Pisao sam pojednostavljeno radi očiglednosti. Ovo znamo iz iskustva,dakle to vrijedi samo kod ove dvije funkcije? Moguće je, ali je onda sigurno mnogo komplikovana.Treba pitati Nedeljka ili Bojana. Ovo izjednačimo s našim izrazom x"=-(2 ni g/l)x ...slijepa ulica.Kako naći omega? U ovaj izraz ubaci opšti oblik za x i x" koji si izračunao.A onda krati lijevo i desno. Ostaće nešto. Ujedno da ispravim sebe: omega T=2 pi , a ne 1. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|