[ eminna @ 06.04.2009. 20:32 ] @
| treba mi objasnjenje ako neko moze pomoc da mi objasni kako se grupisu polinomi pa se rastave ??? i ako moze primjer?? imam test al ne kontam... hvala |
|
[ eminna @ 06.04.2009. 20:32 ] @
[ holononi @ 09.04.2009. 20:36 ] @
Nema univerzalnog rešenja. Poenta je da provežbaš što više zadataka iz knjige koju koristite u školi. Pa šta upamtiš.
Ono što obavezno moraš znati je a^2 - b^2 = (a - b)(a + b) a^3 - b^3 = (a - b)(a^2 + ab + b^2) a^4 = (a^2)^2 AX^2 + BX + C = 0 => X1,2 = ( -B +- Sqrt( B^2 - 4AC ) ) / (2A) Kao i trikovi sa dodavanjem i oduzimanjem potrebnih članova x^4 + x^2 + 1 = x^4 + x^2 + 1 + 0 = (dodamo ništa, pa ništa ni ne menjamo) x^4 + x^2 + 1 + (x^ 2 - x^2) = ( pa opet ništa ne dodamo jer je (x^ 2 - x^2) = 0 ) x^4 + x^2 + 1 + x^ 2 - x^2 = x^2(x^2 + 1) + x^2 + 1 - x^2 = x^2(x^2 + 1) + 1(x^2 + 1) - x^2 = (x^2 + 1)(x^2 + 1) - x^2 = (x^2 + 1)^2 - x^2 = (posle puno vežbe primetićeš da je ovo a^2 - b^2, gde je a = (x^2 + 1) i b = x) [(x^2 + 1) - x][(x^2 + 1) + x] = (x^2 + 1 - x)(x^2 + 1 + x) = (x^2 - x + 1)(x^2 + x + 1) Ima raznih takvih trikova a nezgodno je što naši školski programi zahtevaju da se rešenje prepozna unapred. Zato je potrebno puno rada. [ Nedeljko @ 10.04.2009. 08:00 ] @
Rastavljanje polinoma na činioce je nejasan pojam ako se ne zna šta su prosti faktori. Poznato je da se svaki kompleksan polinom može rastaviti na kompleksne faktore stepena jedan. No, to bi onda radio numerički (mada za konkretnu svrhu obično postoje i druga rešenja). Slično važi i za rastavljanje realnih polinoma na proizvod realnih polinoma, s tim što su onda prosti faktori realni polinomi stepena jedan i realni polinomi stepena dva sa negativnom diskriminantom.
Za rastavljanje raiaonalnog polinoma na proizvod racionalnih polinoma postoji Kronekerov algoritam. [ holononi @ 10.04.2009. 09:08 ] @
Citat: Rastavljanje polinoma na činioce je nejasan pojam... Ja sam pošao od pretpostavke da je u pitanju osmak koji priprema testove za upis u srednju školu. [ Nedeljko @ 10.04.2009. 09:30 ] @
[ holononi @ 10.04.2009. 10:36 ] @
Citat: Voleo bih da vidim rešenja. Baš kao što sam dao primer u mom odgovoru: x^4 + 1 = x^4 + 2x^2 - 2x^2 + 1 = x^4 + 2x^2 + 1 - 2x^2 = (x^2 + 1)^2 - 2x^2 = [(x^2 + 1) - x√2][(x^2 + 1) + x√2] = (x^2 - x√2 + 1)(x^2 + x√2 + 1) x^4 + 4 = 4(x^4/4 + 1) = 4(a^4 + 1), gde je a^4 = x^4/4 (1) U osnovnoj školi se ne rade kompleksni brojevi. (2) Ne dovodi se u pitanje inteligencja kao što naš nakaradni školski sistem (od osnovne do fakulteta i posle) nabija na nos učenicima. Ove primere ili popamtite ili niste zapamtili. Zato sam preporučio što više vežbanja. Trebaju vam samo u školi i nikad više u životu, osim ako ste po profesiji usko vezani za matematiku. (3) Kako Kronekerov algoritam za faktorizaciju polinoma podrazumeva poznavanje (i ne samo poznavanje) interpolacionih polinoma, to bi takvo rešenje bilo nerazumljivo svima osim studentima matematike (boljim). Naravno, ako je pitanje postavio student koji poseduje šira znanja ja se izvinjavam. [ Nedeljko @ 10.04.2009. 10:49 ] @
Polinom
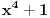 je nerastavljiv nad poljem racionalnih brojeva, ima dva prosta faktora nad poljem realnih brojeva, odnosno četiri nad poljem komleksnih brojeva. je nerastavljiv nad poljem racionalnih brojeva, ima dva prosta faktora nad poljem realnih brojeva, odnosno četiri nad poljem komleksnih brojeva.Ne radi se ovde niokakvoj inteligenciji, već o jednoznačnosti rešenja zadatka. Ako se u osnovnoj školi ne uče kompleksni brojevi, uče se racionalni i realni, pa rešenje nije jednoznačno određeno. A što se tiče inteligencije, pa mora se nekako napraviti razlika između četvorke i petice. Sistem ocenjivanja nije binaran - prošao si ili nisi, već se pravi i neka gradacija. Kada sam ja išao u školu, zvanične definicije ocena su bile: 2 - razumevanje gradiva. 3 - reprodukcija naučenog. 4 - primenjivanje naučenog. 5 - izvlačenje zaključaka. Dakle, u slučaju Talesove teoreme, za 2 si trebao da je ukapiraš, za 3 da umeš da je formulišeš nekako, može i svojim rečima, ali da se na kraju vidi šta se pod kojim uslovom (ako nastavnik preseče prave neparalelnim pravama, Talesova teorema se ne može primeniti) kako odnosi, za 4 da znaš da rešiš zadatak koji se rešava primenom te teoreme (npr. da pomoću senke štapa odrediš visinu Keopsove piramide), a za 5 da rešavaš zadatke sa zvezdicom. [ Nedeljko @ 10.04.2009. 10:57 ] @
Citat: holononi: (3) Kako Kronekerov algoritam za faktorizaciju polinoma podrazumeva poznavanje (i ne samo poznavanje) interpolacionih polinoma, to bi takvo rešenje bilo nerazumljivo svima osim studentima matematike (boljim). Ja sam interpolacioni polinom učio u IV razredu gimnazije iz numeričke matematike. Daleko od toga da to reba da zna samo student matematike. To bi morao da zna i svaki sudent tehnike. Sa druge strane, konstrukcija interpolacionog polinoma je šablon koji se može ugraditi u Kronekerov algoritam. No, slažem se da nije neophodan za đake. Njega sam pomenuo samo zbog izjave da nema univerzalnog rešenja, bez ikakve ograde. Možda ovu temu čita još neko koga baš to zanima, pa mu ovakva informacija može koristiti, takoda smatram da iskazi treba da budu formalno korektni, a ako bi nešto zbunilo postavljača teme, da onda to treba jednostavno preskočiti, tj. prećutati, a nikako davati izjave koje nisu formalno korektne. [ holononi @ 10.04.2009. 13:37 ] @
Citat: Daleko od toga da to reba da zna samo student matematike. Mnogi studenti otaljaju ispite a da im ni mrva nakon toga ne ostave, bilo da su vešti u prepisivanju ili su im se zalomila pitanja koja im odgovaraju. U svakom slučaju i nakon dobro položenog ispita treba očuvati formu da bi se stečeno znanje zaista moglo primeniti u praksi. Citat: To bi morao da zna i svaki sudent tehnike. Kad već pominjemo studente tehnike, pre nekoliko godina sam upoznao studentkinju koja je upravo išla na ispit iz matematike 2 na jednom našem tehničkom fakultetu. I dok smo tako ćaskali u autobusu pogledao sam u knjigu da vidim šta rade. Na prvi mah pitanja su mi se učinila ozbiljnim jer je i meni trebalo nekoliko minuta da ih bez olovke rešim. Oni ne rade pismeni kao što se radi na Prirodno Matematičkom fakultetu (koliko ja znam na svim odsecima), već imaju test na zaokruživanje. a testovi su dati u knjizi. Knjiga ima prijavu za ispit. Knjiga mora da se pokaže profesorici da je ona potpiše i onda može da se koristi na ispitu. Naravno, apsolutno ne sumnjam da ima studenata tehnike koji barataju gradivom koje su odslušali iz matematike. Na kraju da dodam: Odgovori koje sam ponudio sasvim su primereni jednom osmaku koji prati dodatnu nastavu iz matematike, jer je imao prilike da nauči i šta su to racionalni i šta su iracionalni brojevi kao i dokaz da je koren iz dva iracionalan broj i slično. Rastavljanje x^4 + 1 u realnom domenu je dovoljno studentu da položi sve ispite zaključno sa Analizom 2, samo se treba setiti kako se to radi. Nešto više će mu trebati tek kad dodje do Kompleksne Analize. Gotovo da nema matematičkog problema koji se ne može još doterati da rešenje bude bolje. Uostalom, pogledajte u šta se izrodila ova diskusija potekla iz elementarnog pitanja. Medjutim, svi zadaci iz matematike, od kolevke pa do groba, su namešteni. Ti zadaci se rešavaju u odredjenom kontekstu, što nastavnik zna i šepuri se kako je pametan pa učenik stiče utisak da je nešto skrivio jer nikako da ukapira odakle njemu (x^2 - 1) = (x - 1)(x + 1) a to je nešto što jednostavno mora znati "napamet". I tako učenik ne sme da uči "napamet" a nastavnik stalno od njega traži da sve zna "napamet". Na fakultetu je priča ista samo je malo obimnije gradivo. To su jednostavno manipulacije. Kako učenici nigde ne uče posebno algoritam za rastavljanje polinoma, već se sve obavlja "na mišiće" najčešće metodama "proba i greška" to ostaje da samo puno rade i da se naviknu da probavaju dok ne naštimaju rezultat. Ah, da Citat: Kada sam ja išao u školu, zvanične definicije ocena su bile: Nekad bilo, sad se pripovjeda. [ Nedeljko @ 10.04.2009. 13:52 ] @
Rekao sam da bi svaki student tehnike morao da zna da izračuna interpolacioni polinom i stojim iza toga. To što mnogi otaljavaju ispite je protiv argument, koliko je i protivargument da na univerzitetu ima korupcije.
Odgovor da je polinom 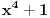 nerastavljiv je isto toliko i primeren i tačan koliko i odgovor da je nerastavljiv je isto toliko i primeren i tačan koliko i odgovor da je 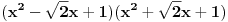 njegova faktorizacija. Dakle, imaš dva suštinski različita, podjednako tačna, odgovora na isto pitanje. To samo znači da sa pitanjem nešto nije u redu. njegova faktorizacija. Dakle, imaš dva suštinski različita, podjednako tačna, odgovora na isto pitanje. To samo znači da sa pitanjem nešto nije u redu.Koliko god ja i ti znali iracionalne, kompleksne i ko zna kakve druge brojeve, polinom 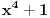 se ne može rastaviti nad poljem racinalnih brojeva. Jednostavno, ne može. To nije pitanje mog ili tvog poznavanja nekih skupova brojeva, niti nečije umešnosti, već jednostavno ne može. Nad poljem realnih brojeva može. No, to su dva potpuno različita zadatka i to treba znati da ne bi dolazilo do zabuna. se ne može rastaviti nad poljem racinalnih brojeva. Jednostavno, ne može. To nije pitanje mog ili tvog poznavanja nekih skupova brojeva, niti nečije umešnosti, već jednostavno ne može. Nad poljem realnih brojeva može. No, to su dva potpuno različita zadatka i to treba znati da ne bi dolazilo do zabuna.[ R A V E N @ 10.04.2009. 15:41 ] @
Citat: Nedeljko: 2 - razumevanje gradiva. 3 - reprodukcija naučenog. 4 - primenjivanje naučenog. 5 - izvlačenje zaključaka. Haha,ovo me podsjetilo na profesora geografije iz gimnazije,naime geografiju su svi smatrali predmetom za nabijanje prosjeka i kada mnogi nisu bili zadovoljni dobijenom ocjenom i napravili prigovor,on je odgovorio: "Šta se bunite,i to je dobro.Evo kako stvari stoje: 2 - vi znate za 2 3 - ja znam za 3 4 - knjiga zna za 4 5 - Bog zna za 5." [Ovu poruku je menjao R A V E N dana 10.04.2009. u 16:54 GMT+1] [ Nedeljko @ 10.04.2009. 16:04 ] @
Znao sam brdo đaka koji su po tim kriterijumi zasluživali 5, a tvoj profa cepe iz prostog razloga što su ocene namenjene isključivo đacima, a ne profesorima, knjigama i bogovima.
[ holononi @ 10.04.2009. 17:36 ] @
Pošto baš insistiraš, još jednom sam pročitao postavljeno pitanje @eminna. Nigde ne vidim ograničenje na racionalne brojeve. Kako nema glupih pitanja a nema ni dodatnih objašnjenja pošao sam od najjednostavnije pretpostavke da je reč o učeniku koji priprema testove za upis u srednju školu. Kakvi zadaci se javljaju na tim testovima? Zadaci sa integralnim jednačinama? Banahovi prostori? Sigma algebre? Ma daj malo da sidjemo na zemlju. Odgovorimo na najjednostavnije pitanje pa ako asker nije zadovoljan, pitaće još. Kako se @eminna ne oglašava to znači ili je pronašla rešenje, ili je zadovoljna nekim od odgovora ili je problem odložila za kasnije radi drugih obaveza.
Iz izraza "grupisu polinomi pa se rastave" zaključio sam da je reč o osobi koja nije prošla neku dublju obuku u vezi polinoma jer bi student fakulteta rekao "grupisu ČLANOVI polinomi". Sledi da je @eminna osoba koja slabo poznaje tu oblast, pa je verovatno reč o nekome ko je ili katastrofalno loš student ili početnik odnosno osnovac ili u najboljem slučaju prvi srednje. Bilo kako bilo, zaključio sam da je u odgovoru @eminna potreban elementaran pristup. U osnovnoj školi se rade zadaci sa realnim brojevima. Da bih to proverio evo uzimam jednu zbirku rešenih zadataka namenjenu naprednijim učenicima VIII razreda. Knjigu su potpisala 4 autora od kojih jedan doktor nauka a jedan od recenzenata je moj profesor geometrije. Pa ako oni nisu u pravu nisam ni ja. Pronašao sam poglavlje "Rastavljanje polinoma na činioce" što odgovara postavljenom pitanju. Tu pronalazim tri tipa zadataka: - Rastavljanje izdvajanjem zajedničkog činioca, - Rastavljanje razlike kvadrata, - Rastavljanje kvadratnog trinoma. To otprilike odgovara sugestiji o rešvanju takvih zadataka koju sam izneo u prvom odgovoru na polazno pitanje. Takodje evo i jednog zadatka iz knjige: Rastaviti na činioce: √21 - 3 čije rešenje takodje pronalazim u knjizi: √3(√7 - √3) I tako, ni √3 ni √7 nisu bili racionalni brojevi dok sam išao u školu, pa valjda ni danas nisu. Sledi učenicima osnovne škole se daju zadaci sa iracionalnim brojevima. Medjutim nigde u knjizi ne nalazim zadatke sa kompleksnim brojevima, iako ima primera koji bi za potpuno rastavljanje zahtevali kompleksna rešenja. Na primer: x^3 + 2x^4 + 4x^2 + 2 + x sa rešenjem: (2x^2 + x + 2)(x^2 + 1) Nema kompleksnih rešenja, ne zato što to moj profesor ne zna da reši, već zato što to nije predvidjeno gradivom za osnovnu školu. Podrazumeva se da rešenje treba da bude realno jer su učenici fokusirani na realne brojeve. A kompleksna rešenje će naučiti u trećem srednje i onda rešenje navedeno u knjizi za VIII razred neće biti za 5 već za 3. [ Nedeljko @ 11.04.2009. 08:48 ] @
Citat: holononi: Pošto baš insistiraš, još jednom sam pročitao postavljeno pitanje @eminna. Nigde ne vidim ograničenje na racionalne brojeve. Nema ni ograničavanja na realne brojeve. A pitanje nad koji skupom mogućih koeficijenata se vrši rastavljanje nije glupo, već eliminiše dvosmislenosti. Nije to matematička perverzija koju su izmislili dokoni matematičari, već esencijalni deo formulacije i rešenja. Bez toga ni broj faktora nije jednoznačno određen. Citat: holononi: Kako nema glupih pitanja a nema ni dodatnih objašnjenja pošao sam od najjednostavnije pretpostavke da je reč o učeniku koji priprema testove za upis u srednju školu. A ja sam pošao od još jednostavnije pretpostavke da postavljač pitanja najbolje zna šta mu treba. Citat: holononi: Takodje evo i jednog zadatka iz knjige: Rastaviti na činioce: √21 - 3 čije rešenje takodje pronalazim u knjizi: √3(√7 - √3) Ne vidim zašto rešenje ne bi moglo da bude 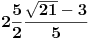 ili ili 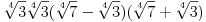 . Šta se tu prihvata kao skup mogućih činilaca? Ako to nigde ne piše, knjiga je divna i nije čudo što đaci ne mogu iz takvih knjiga ništa da nauče sa razumevanjem. Ima li takvih zadataka u američkom, nemačkom, ruskom ili francuskom obrazovnom sistemu ili su takvi zadaci domaći "biser"? . Šta se tu prihvata kao skup mogućih činilaca? Ako to nigde ne piše, knjiga je divna i nije čudo što đaci ne mogu iz takvih knjiga ništa da nauče sa razumevanjem. Ima li takvih zadataka u američkom, nemačkom, ruskom ili francuskom obrazovnom sistemu ili su takvi zadaci domaći "biser"?[ zzzz @ 11.04.2009. 09:47 ] @
Slažem se sa @holononi u potpunosti.
I ne samo to nego mislim da se takvoj djeci sa mnogo šupljina u predznanju mora prići sa najjednostavnijim zadacima. Naprimjer: -Razlika kvadrata a^2+b^2=(a-b)(a+b) 1)Insistirati da se to zapamti napamet. 2)Nacrtati geometrijsku slikicu, od većeg kvadrata isjeći manji, pa pokazati da se može napraviti pravougaonik od tog ostatka.Dati priliku da dijete skuži kolike su stranice tog pravougaonika, i poveže to sa zapamćenom jednačinom. 3)Naučiti dijete da množi (a+b) sa (a-b). 4)Zadati da samostalno riješi nešto ovako: M^2-N^2=? i slični zadaci. Ovo je dovoljno posla za jedan dan, s tim da sve treba ponoviti bar na kratko u narednih nekoliko dana. Naravno da ovo ne vrijedi za napredne đake kojih obično nema više od 3 u razredu. [ Kolins Balaban @ 11.04.2009. 10:57 ] @
i ja se slazem sa kolegom @holononi. kad se kaze rastaviti neki polinom na faktore, onda se i podrazumjeva da ti faktori budu sto jednostavniji, i da rjesenje bude prosto. nedeljkova rjesenja su tacna, ali nisu nimalo prosta, niti su jedina, niti ih moze skuziti neko, ko postavlja ovako jednostavan zadatak. nedeljko, kao neko ko se bavi matematikom, a mozda i predaje djacima, iz same postavke problema treba zakljuciti kakvo rjesenje treba ponuditi, i o kakvoj se osobi radi i sa kakvim znanjem iz matematike. mislim da se previse threadova na ovom podforumu previse zaspamalo, ulazeci previse u sutinu i kojekakve rasprave, koje ni najmanje ne pomazu onom ko postavi problem. nedeljko i @holononi mogu svoje tjerati dokle su zivi, ali to ni najmanje nece pomoci nekome ko ne zna rastaviti polinom na faktore, samo ce ga jos vise zbuniti.
[ Goran Rakić @ 11.04.2009. 11:04 ] @
Kako da rastaviš nešto na proste faktore ako ne znaš šta su prosti faktori? Šta znači "da rešenje bude prosto"? U školi između ostalog treba naučiti i formalno i koncizno izražavanje.
[ Kolins Balaban @ 11.04.2009. 11:10 ] @
vrlo jednostavan odgovor ;) ovo rjesenje nije prosto:
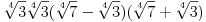 (nisam nigdje spomenuo proste faktre, nego prosto rjesenje) mislim da znas o cemu ja pricam. kad dobijes neko rjesenje koje, da tako kazem, "nije fino" onda se zapitas da li je ono i tacno. obicno se rjesenja stimaju da budu fina, okrugli brojevi itd itd... s ovom temom sam zavrsio, posto dalja rasprava nece pomoci nikome. (nisam nigdje spomenuo proste faktre, nego prosto rjesenje) mislim da znas o cemu ja pricam. kad dobijes neko rjesenje koje, da tako kazem, "nije fino" onda se zapitas da li je ono i tacno. obicno se rjesenja stimaju da budu fina, okrugli brojevi itd itd... s ovom temom sam zavrsio, posto dalja rasprava nece pomoci nikome.[ Goran Rakić @ 11.04.2009. 11:22 ] @
Ako ne razumeš postavku zadatka, već tražiš "fine brojeve", pašćeš kao kruška na sledećem testu:
Citat: Argumentovano procenjivanje nam je potrebno i kad kupujemo polikolor za krečenje stana i kad bankama ukidamo određenu vrstu kredita da bi inflacija ostala na zacrtanom nivou. Sa druge strane, ukoliko na osnovu podataka sa kojima raspolažemo nije moguće napraviti dobru procenu, onda to treba reći jasno i glasno. Nažalost, ta se sposobnost kod đaka inhibira sve vreme školovanja. Kapacitet te besmislenosti se najbolje vidi na zadacima kao što je ovaj: "U stadu ima 125 ovaca i 5 pasa ovčara. Koliko godina ima čobanin?" Istraživanja pokazuju da na ovo pitanje čak tri četvrtine učenika nižih razreda daje brojčani odgovor! Transkript koji je načinjen tokom jednog ovakvog ispitivanja otkriva određenu vrstu pogrešne slike o svrsi matematike koju, očigledno, ima većina dece: "125+5=130... to je previše, 125-5=120 je opet previše... ali 125/5=25. To ima smisla! Ja mislim da čobanin ima 25 godina!" Izvor: B92 Nauka. [ holononi @ 11.04.2009. 16:07 ] @
Citat: Ne vidim zašto rešenje ne bi moglo da bude Pa kad već demonstriramo silu  PS Hteo sam da rastopim i trojku, ali mi je ekran mali. [Ovu poruku je menjao holononi dana 11.04.2009. u 21:04 GMT+1] [ Nedeljko @ 11.04.2009. 18:02 ] @
Citat: Kolins Balaban: vrlo jednostavan odgovor ;) ovo rjesenje nije prosto: 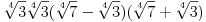 (nisam nigdje spomenuo proste faktre, nego prosto rjesenje) mislim da znas o cemu ja pricam. kad dobijes neko rjesenje koje, da tako kazem, "nije fino" onda se zapitas da li je ono i tacno. obicno se rjesenja stimaju da budu fina, okrugli brojevi itd itd... s ovom temom sam zavrsio, posto dalja rasprava nece pomoci nikome. (nisam nigdje spomenuo proste faktre, nego prosto rjesenje) mislim da znas o cemu ja pricam. kad dobijes neko rjesenje koje, da tako kazem, "nije fino" onda se zapitas da li je ono i tacno. obicno se rjesenja stimaju da budu fina, okrugli brojevi itd itd... s ovom temom sam zavrsio, posto dalja rasprava nece pomoci nikome.A zašto je 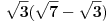 prostije od prostije od 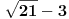 ? ?Citat: zzzz: I ne samo to nego mislim da se takvoj djeci sa mnogo šupljina u predznanju mora prići sa najjednostavnijim zadacima. Naprimjer: -Razlika kvadrata a^2+b^2=(a-b)(a+b) 1)Insistirati da se to zapamti napamet. 2)Nacrtati geometrijsku slikicu, od većeg kvadrata isjeći manji, pa pokazati da se može napraviti pravougaonik od tog ostatka.Dati priliku da dijete skuži kolike su stranice tog pravougaonika, i poveže to sa zapamćenom jednačinom. 3)Naučiti dijete da množi (a+b) sa (a-b). 4)Zadati da samostalno riješi nešto ovako: M^2-N^2=? i slični zadaci. Ovo je dovoljno posla za jedan dan, s tim da sve treba ponoviti bar na kratko u narednih nekoliko dana. Ovo je skroz OK, ali nema veze sa onim o čemu pričamo. Najteži su oni zadaci kod kojih treba gledati u pasulj šta neko od tebe očekuje. Imao sam na fakultetu problema na ispitu sa jednim takvim nedorečenim asistentom. Zada zadatak iz parcijalnih jednačina koji se lako rešava primenom kompleksne analize, a onda kaže "Nemojte koristiti KA, osim nešto malo, elementarno.". I onda sam ja trebao da pogađam šta je on zamislio, jer nije hteo da kaže. Pitao sam, može li ovo, može li ono, trt mrt, da bi se na kraju ispostavilo da se smeju koristiti Koši-Rimanovi uslovi. Pre toga je na ispitu iz DJ zadao zadatak za koje prirodne brojeve  postoji diferencijalna jednačina oblika postoji diferencijalna jednačina oblika  takva da važi neki uslov vezan za rešenja. Nije hteo da kaže kojoj klasi funkcija treba da pripada funkcija takva da važi neki uslov vezan za rešenja. Nije hteo da kaže kojoj klasi funkcija treba da pripada funkcija  , a rešenje je bitno zavisilo od toga da li je to klasa neprekidnih ili Lipšicovih funkcija. Posle ispita se ispostavilo da je mislio na Lipšicove. , a rešenje je bitno zavisilo od toga da li je to klasa neprekidnih ili Lipšicovih funkcija. Posle ispita se ispostavilo da je mislio na Lipšicove.Ovakvim pristupom đaci mogu samo da nauče da je nešto "ono što nastavnik radi onako" i onda se čudimo zašto matematiku ne razumeju i na kraju ne umeju da je primene u praksi, jer se matematika predaje na način na koji se ne može razumeti. PISA testovi sve pokazuju. [ holononi @ 11.04.2009. 20:31 ] @
Citat: A zašto je √3(√7 - √3) prostije od √21 - 3 ? Ne kažem da je prostije, samo je rastavljeno na činioce. Uostalom šta je prostije (a^2 - b^2) ili (a - b)(a + b)? Inače tema je "Rastavljanje polinoma na faktore", pa kad pogledamo u Wikipedia enciklopediju Citat: Factoring is the decomposition of an object (for example, a number, a polynomial, or a matrix) into a product of other objects, or factors, which when multiplied together give the original. vidi se da navedeno rešenje odgovara datoj definiciji, neki objekat je razložen u proizvod drugih objekata čijim množenjem opet daju original. A pogledaj ovo razlaganje na proste činioce: 18 = 2 * 3^2, da ne pišem opštu formulu. Citat: I onda sam ja trebao da pogađam šta je on zamislio, jer nije hteo da kaže. Naravno da nije hteo da ti kaže, naš sistem školovanja ne služi učenicima-studentima već filmskim zvezdama da budu još veće filmske zvezde. Tako je na svim nivoima [ Nedeljko @ 11.04.2009. 21:04 ] @
A kako bi rastavio broj 2 na činioce? Vidiš, i proizvod koji se sastoji od samo jednog činioca je proizvod, pa je u tom kontekstu i
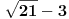 jedna faktorizacija tog broja. Ako se zadatak sastoji samo u tome da se nađe barem jedna faktorizacija nečega, onda uvek postoji trivijalno rešenje - taj objekat u proizvodu daje sebe. jedna faktorizacija tog broja. Ako se zadatak sastoji samo u tome da se nađe barem jedna faktorizacija nečega, onda uvek postoji trivijalno rešenje - taj objekat u proizvodu daje sebe.Prirodni brojevi se tipično rastavljaju na proste činioce da bi se znalo sa čim su deljivi, sa čim uzajamno prosti itd. Dakle, zahtev da činioci budu prosti proističe iz primene. Ako je primena takva da zahteva neke druge uslove, rešavaće se ti drugi uslovi, a ovakva "matematika" koja nema kontekst i koja se može "shvatiti" samo uz konzumiranje teških droga vodi gubljenju razlike između matematike i numerologije. [ petarm @ 11.04.2009. 21:38 ] @
Svidja mi se ova rasprava. Koliko se ja secam rastavljanje polinoma na proizvod prostih cionilaca se radi u 7 razredu! Pitanje je kako objasniti detetu koje je 7 razred sta znaci prosti cinilac? Mozda treba izbaciti ovo prosti. To moze decu samo da zbuni. Jel ce razmisljati mozda kako je dodjavola
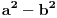 slozenije od slozenije od 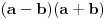 ? ? 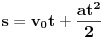 Uopsteno ovo je za nepoznatu  kvadratna jna, ali se moze namestiti na neku jednostavnu koja se moze resiti izdvajanjem zajednickog cinioca ispred zagrade i grupisanjem clanova. Npr. lupam kvadratna jna, ali se moze namestiti na neku jednostavnu koja se moze resiti izdvajanjem zajednickog cinioca ispred zagrade i grupisanjem clanova. Npr. lupam 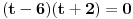 ; ;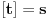 i odbaciti resenje t=-2s jer nema fizickog smisla i ostaviti resenje i odbaciti resenje t=-2s jer nema fizickog smisla i ostaviti resenje 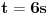 . . [ holononi @ 11.04.2009. 21:57 ] @
Citat: A kako bi rastavio broj 2 na činioce? 2 = Pi * cos(Pi/4) * cos(Pi/8) * cos(Pi/16) * cos(Pi/32) * ... * cos(Pi/2^n) * ... [ Kolins Balaban @ 11.04.2009. 22:35 ] @
ne mogu da se ne javim. postoje dva problema. prvi je, kako neki polinom rastaviti na cinioce, a drugi problem je, zasto to rastavljamo i zasto nam to treba. kad ce nam trebati da broj 2 rastavimo na cinioce? mozes pomnoziti n puta n-ti korjen iz dva, i eto rastava. sto ce nam to? odgovor je jednostavan. da nekom studentu ili uceniku zagorcamo zivot ;)
[ holononi @ 12.04.2009. 09:50 ] @
Citat: zasto to rastavljamo i zasto nam to treba Treba onima koji se bave teorijskom matematike i onima koji u svom radu obilno primenjuju praktično ili teorijski različite matematičke metode. Na primer hemičari ili fizičari često koriste interpolacione i ekstrapolacione polinome, splajnove i oni definitivno moraju da razmeju tako proste stvari kao što je (elementarno) rastavljanje polinoma. Slično je i sa biolozima, ekonomistima itd. Ekonomisti imaju posebne ispite poput "matematičke metode u ekonimiji" i slično i to ne zato da bi nezaposleni profesori bili zaposleni, već to ima praktičnu primenu. Ovo sve se odnosi na poslove za koje se traži lice sa završenim fakultetom. Druga je priča kad su u pitanju poslovi koje obavljaju lica sa srednjom stručnom spremom. I tu je pitanje obima i šta im sve treba. Jedan ekonomski tehničar sigurno neće rastavljati polinome ili rešavati integrale dok knjiži otpremnice i vrši kalkulaciju cena. Medjutim, vi nikad unapred ne znate kuda će krenuti neko ko je u osnovnoj školi, pa i u srednjoj. Uzmimo primer: šta će jednom bravaru grupe, kompleksni brojevi i da ne nabrajam, sve ima u njihovoj knjizi iz matematike i predvidjeno planom i programom. Zar nije dovoljno da nauče nešto o izračunavanju površine i zapremine osnovnih figura i tela? Pa... verovatno je tako. To je jedna strana medalje. Sa druge strane lično znam osobe koje su tavorile kao srednješkolci u zanatskim odeljenjima upravo bravara i automehaničara a nakon toga su završili višu tehničku školu. Ima i ko posle zanata završi fakultet. Šta sad? Kako pet ili desed godina unapred selektovati učenike na one koji će jednog dana postati akademski gradjani i na one kojima ćemo nabiti na nos da su "glupavi idioti" pa se i kroz zanat provlače? U svakom slučaju naš školski sistem je neprimeren sadašnjem trenutku i potrebama društva. Puno je rigidan i moraće da se prilagodi. Kako? Treba pogledati kako to rade napredniji od nas. [Ovu poruku je menjao holononi dana 12.04.2009. u 13:28 GMT+1] [ Nedeljko @ 12.04.2009. 10:38 ] @
Citat: holononi: 2 = Pi * cos(Pi/4) * cos(Pi/8) * cos(Pi/16) * cos(Pi/32) * ... * cos(Pi/2^n) * ... E, ovo mi se sviđa. Daš đacima zadatak iz faktorizacije zamislivši jedno od rešenja i podeliš kečeve svima koji napišu nešto drugo. Ako nisam bio dovoljno jasan, mislio sam na faktorizaciju broja 2 onako kako se radi u školi (faktorizacija prirodnih brojeva). Do ovakvih "rešenja" se dolazi kada se ne zna šta se zapravo rešava. Citat: holononi: Treba onima koji se bave teorijskom matematike i onima koji u svom radu obilno primenjuju praktično ili teorijski različite matematičke metode. Faktorizacija je izmišljena zato što se neko bavi teorijskom matematikom. Naprotiv. Faktorizacija je izmišljena zbog ovoga. Citat: petarm: A zasto se ovo radi? Dati primer iz fizike. Posto u 7 razredu na fizici rade jednako-ubrzano kretanje materijalne tacke po pravoj liniji: 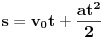 Uopsteno ovo je za nepoznatu  kvadratna jna, ali se moze namestiti na neku jednostavnu koja se moze resiti izdvajanjem zajednickog cinioca ispred zagrade i grupisanjem clanova. Npr. lupam kvadratna jna, ali se moze namestiti na neku jednostavnu koja se moze resiti izdvajanjem zajednickog cinioca ispred zagrade i grupisanjem clanova. Npr. lupam 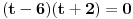 ; ;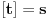 i odbaciti resenje t=-2s jer nema fizickog smisla i ostaviti resenje i odbaciti resenje t=-2s jer nema fizickog smisla i ostaviti resenje 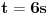 . .Dakle, da bi se snizio stepen algebarske jednačine koja se rešava, tj. da bi se rešavanje jedne složenije jednačine svelo na rešavanje više prostijih i onda nema onakvih faktorizacija dvojke za koje niko ne zna čemu služe, osim tamo gde takav razvoj zaista obavlja posao. [ Nedeljko @ 12.04.2009. 10:42 ] @
Citat: holononi: Lim(n -> ∞)( n * ⁿ√2 ) = ∞ <> 2 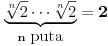 . .Kolins Balaban je bio u pravu, ali si pogrešno protumačio ono što je napisao. [ holononi @ 12.04.2009. 12:00 ] @
Citat: E, ovo mi se sviđa. Daš đacima zadatak iz faktorizacije zamislivši jedno od rešenja i podeliš kečeve svima koji napišu nešto drugo. Ova faktorizacija nije namenjena ni srednjoškolcima ni osnovcima. Kakvu faktirizaciju treba očekivati od učenika osnovne škole već sam opisao u prvom postu a upravo je @Nedeljko dobio faktorizaciju dvojke onako kako je tražio. Uostalom, neko ko se u diskusiji poziva na Lipšic-a ne deluje mi kao neko naivno djače. Citat: Faktorizacija je izmišljena zbog ovoga. Ne znam zbog čega je izmišljena, ali oko nečega možemo da se složimo. Ako @Nedeljko pažljivo pročita moj prethodni post videće da se i ja pozivam na potrebe fizičara. [Ovu poruku je menjao holononi dana 12.04.2009. u 14:05 GMT+1] [ holononi @ 12.04.2009. 12:24 ] @
@Kolins Balaban
Izvinjavam se zbog pogrešno protumačenog navoda. Izbacio sam taj deo iz posta. [ Nedeljko @ 13.04.2009. 11:02 ] @
Da, video sam da si pominjao primene matematike i to je u redu. Ja sam mislio, kako na matematičke, tako i nematematičke primene matematike, ali nije u tome suština.
Faktorizacija se ne radi nad poljima jer nema smisla. Sve što možeš reći je da je proizvod nekih elemenata jednak nekom elementu. One faktorizacije broja 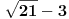 koje sam ponudio su ravnopravne sa bilo kojim drugim proizvodom koji je jedanak tom broju. koje sam ponudio su ravnopravne sa bilo kojim drugim proizvodom koji je jedanak tom broju.Faktorizacija prirodnih brojeva na proste činioce je već nešto drugo, jer se zna šta su prosti elementi. Jedina fakorizacija jedinice u skupu N je prazan proizvod, a jedina fatorizacija bilo kog prostob broja je proizvod od samo jednog elementa, dakle, sam taj prost broj. Poenta je bila da je i proizvod od samo jednog elementa proizvod (zato sam pominjao dvojku), pa da je samim tim i 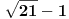 ravnopravana faktorizacija ravnopravana faktorizacija Kad bi se matematika predavala tako da se uvođenje svih pojmova motiviše, onda ne bi bilo ovakvih besmislica. [ Cabo @ 13.04.2009. 11:31 ] @
Ova diskusija mi deluje kao nastavak priče koja se povela na ovoj temi o Logici. Kao što sam tu rekao, mislim da je opšti problem školstva u Srbiji prekomerno insistiranje na "naučnosti" nauštrb didaktičnosti, kao naporu da se materija približi učenicima. Prosto rečeno, niko se naučen nije rodio, i niko prosečnih sposobnosti se nije naučio tako što je odmah krenuo "s neba pa u rebra" sa "teškom artiljerijom" kakva se uči na fakultetu. Smatram da treba prvo krenuti od najosnovnijih stvari i njih dobro utvrditi, a tek onda se otvara put ka onim komplikovanijim. Međutim, problem je što je stručnjacima teško da se "spuste na nivo" učenika, i upravo to odvaja dobre nastavnike od loših.
[ R A V E N @ 13.04.2009. 12:01 ] @
Slažem se,samo što se na univerzitetima nema vremena kvalitetno i smisleno približavati studentima gradivo.Osim ako nije neko darovit,onda je studiranje rutina.
Mislim da su uspješni studenti na tehničkim fakultetima uspješni zato što više-manje površinski apsorbiraju gradivo sa predavanja i vježbi,bez da stvaraju neku globalniju,potpuniju i povezaniju predstavu,nego kad se recimo uči iz 400 strana duge knjige.Sve je nešto u skriptama,ogoljeno do same suštine. Ono šro mi smeta na mom fakultetu je to da se prvenstveno oslanjaju na pisanje u svesku nasuprot učenju iz knjige. [ Nedeljko @ 13.04.2009. 14:01 ] @
Citat: Cabo: Ova diskusija mi deluje kao nastavak priče koja se povela na ovoj temi o Logici. Kao što sam tu rekao, mislim da je opšti problem školstva u Srbiji prekomerno insistiranje na "naučnosti" nauštrb didaktičnosti, kao naporu da se materija približi učenicima. Prosto rečeno, niko se naučen nije rodio, i niko prosečnih sposobnosti se nije naučio tako što je odmah krenuo "s neba pa u rebra" sa "teškom artiljerijom" kakva se uči na fakultetu. Smatram da treba prvo krenuti od najosnovnijih stvari i njih dobro utvrditi, a tek onda se otvara put ka onim komplikovanijim. Međutim, problem je što je stručnjacima teško da se "spuste na nivo" učenika, i upravo to odvaja dobre nastavnike od loših. Na toj temi si bio delimično u pravu, s tim što se ne slažem da definicije treba objašnjavati, već da ih treba motivisati. Takođe, ne mislim da su didaktički i stručni ciljevi u bilo kakvoj suprotnosti. Primer: Deco, može li neko da reši jednačinu 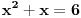 ? A može li neko da reši jednačinu ? A može li neko da reši jednačinu 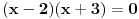 ? Da li jednačine ? Da li jednačine 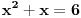 i i 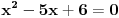 imaju neko zajedničko rešenje? A jednačine imaju neko zajedničko rešenje? A jednačine 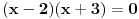 i i 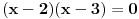 ? E, vidite, ovaj oblik polinoma nam je često podesniji od ovog drugog. Nakon rešavanja ovih problema faktorizacijom, ali bez pominjanja reči "faktorizacija" ide formalan deo. ? E, vidite, ovaj oblik polinoma nam je često podesniji od ovog drugog. Nakon rešavanja ovih problema faktorizacijom, ali bez pominjanja reči "faktorizacija" ide formalan deo.E, onda ne bi bilo bemislica tipa "Faktorisati izraz 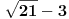 ." i pojmovi bi se zaista i razumeli i umeli primenjivati. ." i pojmovi bi se zaista i razumeli i umeli primenjivati.[ holononi @ 13.04.2009. 16:07 ] @
Citat: E, onda ne bi bilo bemislica tipa "Faktorisati izraz Defincija faktorizacije koju sam usvojio može se naći u Wikipedia enciklopediji. Smatram da je Wikipedia autoritet koji prevazilazi sve naše malenkosti na ovom forumu. U smislu Wikipedia definicije faktorizacije (√21 - 3) je objekat a prozvod nekih drugih objekata koji daju (√21 - 3) je faktorizacija objekta (√21 - 3). Po toj definiciji mogu faktorisati i 2 u skupu celih brojeva 2 = (-1)(-2) A ako treba evo i faktorizacije jedinice u skupu prirodnih brojeva 1 = [ (n + 1) mod n ][ n mod (n - 1) ], n > 1 pa u oba slučaja konstruisan je proizvod različitih elemenata ! [ Nedeljko @ 14.04.2009. 09:16 ] @
Možeš da se klanjaš wikipediji do zemlje, to je tvoja stvar. Stručnjak se ne postaje ni preko jedne enciklopedije, već preko stručne (a ne opšte) literature. Istraživači se sigurno ne informišu iz wikipedije.
Nalazio sam ja po wikipediji netačnosti kao npr. da je složenost računanja broja  nekim algoritmom jednaka nekim algoritmom jednaka 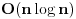 , što svakako nije slučaj, već je složenost najbržih poznatih algoritama jednaka , što svakako nije slučaj, već je složenost najbržih poznatih algoritama jednaka 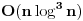 . No, u ovom slučaju o kome raspravljamo wikipedija nije toliko loša. U wikipediji ne piše da se proizvod mora sastojati od najmanje dva faktora. . No, u ovom slučaju o kome raspravljamo wikipedija nije toliko loša. U wikipediji ne piše da se proizvod mora sastojati od najmanje dva faktora.Međutim, ne reče ti meni šta je faktorizacija broja 2 u skupu prirodnih brojeva. Kad to budeš shvatio, onda možeš razumeti i šta su faktorizacije broja 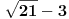 a dotle ne pomaže ni wikipedija. a dotle ne pomaže ni wikipedija.Wikipediju smatram odličnom enciklopedijom, ali svakako ne smatram da joj se može slepo verovati i da se sve sa nje može nekritički prihvatati. Člankena njoj pišu ljudi koji misle da nešto znaju. No, i pored toga ona je dosta kvalitetnija od konkurentskih, ali svakako da nijedan izvor ne pomaže protiv nerazumevanja. [ holononi @ 14.04.2009. 13:23 ] @
Citat: Stručnjak se ne postaje ni preko jedne enciklopedije Ko se hvalio da je stručnjak? Uostalom, šta očekuješ od nekoga koga su izbacili iz škola posle četiri osnovne... [ Nedeljko @ 14.04.2009. 14:06 ] @
Nemam pojma o čemu ti to, ali sam morao da prokomentarišem ovo:
Citat: holononi: Defincija faktorizacije koju sam usvojio može se naći u Wikipedia enciklopediji. Smatram da je Wikipedia autoritet koji prevazilazi sve naše malenkosti na ovom forumu. Ja se sa tim ne slažem i ne prihvatam autoritete kao argument u stručnoj raspravi. [ holononi @ 14.04.2009. 16:06 ] @
Citat: Nalazio sam ja po wikipediji netačnosti kao npr. da je složenost računanja broja nekim algoritmom jednaka , što svakako nije slučaj, već je složenost najbržih poznatih algoritama jednaka . A da li govorite o istim algoritmima? [Ovu poruku je menjao holononi dana 14.04.2009. u 18:25 GMT+1] [ Nedeljko @ 14.04.2009. 16:11 ] @
Da, pa? wikipedia nije savršena. Šts s tim?
[ holononi @ 14.04.2009. 17:27 ] @
Pukla mi je veza, dopunio sam prethodnu poruku.
[ Nedeljko @ 15.04.2009. 08:19 ] @
Trenutno nije poznat brži algoritam od algoritma Čudnovskog. Nije bio problem u tome, ali više ne uspevam da nađem taj iskaz. Izgleda da su ga makli.
[ Nedeljko @ 15.04.2009. 13:59 ] @
Ne mogu sa sigurnošću da tvrdim da li su dali složenost uopšteno u smislu najbržeg poznatog algoritma, ne specificirajući ga, ili su pomenuli i algoritam na koji se to odnosi, ali svakako danas nije poznat alhgoritam koji ima složenost koju su naveli.
[ holononi @ 15.04.2009. 23:27 ] @
Citat: ali svakako danas nije poznat alhgoritam koji ima složenost koju su naveli. Naprotiv, Bailey, Borwein i Plouffe su konstruisali algoritma za izračunavanje broja Pi vremenske složenosti O( n ) i prostorne složenosti O( ln(n) ). U 25 koraka daje 45 miliona cifara broja Pi. Kad budem imao malo više slobodnog vremena proveriću (ako se dual pentijum ne zapali od tolikog računa). [ R A V E N @ 16.04.2009. 01:19 ] @
Ohoho,tema se pravo usijala.Uglavnom kako god,naučio sam par stvari.
Citat: Nedeljko:Izgleda da su ga makli. Ima u historiji članka. Citat: Nedeljko:5 - izvlačenje zaključaka Često je suština ovakvih zadataka(sa zvjezdicom) primjeniti neki metod iz neke potpuno druge oblasti matematike u odnosu na oblast u koju posmatrani problem spada. [Ovu poruku je menjao R A V E N dana 16.04.2009. u 02:32 GMT+1] [ Nedeljko @ 16.04.2009. 07:58 ] @
Citat: holononi: Naprotiv, Bailey, Borwein i Plouffe su konstruisali algoritma za izračunavanje broja Pi vremenske složenosti O( n ) i prostorne složenosti O( ln(n) ). U 25 koraka daje 45 miliona cifara broja Pi. Kad budem imao malo više slobodnog vremena proveriću (ako se dual pentijum ne zapali od tolikog računa). Ako misliš na ovako nešto 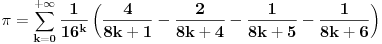 http://en.wikipedia.org/wiki/C...g_Pi#BBP_formula_.28base_16.29 http://en.wikipedia.org/wiki/B...orwein%E2%80%93Plouffe_formula taj algoritam nema složenost koju pominješ za računanje prvih n decimala broja  , već je na toj formuli zasnovan efikasan algoritam za računanje n-te decimale broja , već je na toj formuli zasnovan efikasan algoritam za računanje n-te decimale broja  . Vidi . Vidihttp://en.wikipedia.org/wiki/C...ng_pi#Digit_extraction_methods Kako inače misliš da postigneš prostornu složenost koja je ispod linearne, kada rezultat zauzima linearno mnogo prostora? Izdvajanje jedne cifre je druga stvar. Inače, najbrži programi za računanje broja  za koje znam, a koje možeš naći za Windows su PiFast i QuickPi. za koje znam, a koje možeš naći za Windows su PiFast i QuickPi.http://numbers.computation.fre...onstants/PiProgram/pifast.html http://members.shaw.ca/francislyster/pi/pi.html [ holononi @ 16.04.2009. 08:45 ] @
Citat: Drago mi je da se i ti pozivaš na Wikipedia. To je upravo ono što sam imao na umu. JAVNOST je najveći autoritet. Veći od bilo kakvih doktorata i ko zna kakvih diploma i počasti uručenih u polumračnim kancelarijama. U tom smislu je Wikipedia autoritet koji se uvek mora respektovati. Jer stranice Wikipedia dnevno posećuje možda i na milione ljudi širom sveta. Pred tolikom navalom autor će teško doživeti jutro pišući gluposti. Uostalom i ovu našu prepisku prate mnogi sa strane, pozdrav @R A V E N i ostalima koji samo prate (za sada). PS Stavovi koje sam izneo u vezi algoritama za izračunavanje broja Pi zasnovani su na originalnim tekstovima autora od pre 10-tak godina a ne na Wikipedia materijalu. [ Nedeljko @ 16.04.2009. 10:21 ] @
Čekaj, gde sam ja napisao da je vikipedija loša? Je li ovde
Citat: Nedeljko: Wikipediju smatram odličnom enciklopedijom, ali svakako ne smatram da joj se može slepo verovati i da se sve sa nje može nekritički prihvatati. Člankena njoj pišu ljudi koji misle da nešto znaju. No, i pored toga ona je dosta kvalitetnija od konkurentskih, ali svakako da nijedan izvor ne pomaže protiv nerazumevanja. Dakle, daleko od toga da je loša, ali nije za slepo prihvatanje, kao ni drugi izvori, a univerzitetski udžbenici i prava stručna literatura bi trebali da budu kredibilniji izvori od vikipedije. [ Nedeljko @ 16.04.2009. 10:27 ] @
Citat: holononi: Stavovi koje sam izneo u vezi algoritama za izračunavanje broja Pi zasnovani su na originalnim tekstovima autora od pre 10-tak godina a ne na Wikipedia materijalu. Po svoj prilici ih nisi razumeo. Daj da ih pogledamo. Ne možeš na spektrumu da izračunaš milion decimala npr. broja e, kad spektrum ne može čak ni da memoriše toliki rezultat. Idvajanje jedne cifre je nešto drugo. Takođe, i u naučnim radovima ima grešaka, ali ne verujem da je to slučaj, jer bi to bila početnička greška (da bilo prostorna bilo vremenska složenost izračunavanja bude niža od prostorne složenosti rezultata). BBP je poznat algoritam u matematici po izdvajanju n-te cifre broja  , pri čemu n može daleko da prevazilazi broj bajtova memorije računara. , pri čemu n može daleko da prevazilazi broj bajtova memorije računara.[ holononi @ 17.04.2009. 08:31 ] @
Citat: Po svoj prilici ih nisi razumeo. Daj da ih pogledamo. Kako @Nedeljko tvrdi da BBP algoritam računa n-tu cifru broj Pi, dok autori algoritma u svom tekstu tvrde da ne samo što njihov algoritam računa n-tu cifru broja Pi, već i da su izračunali broj Pi na 45 miliona cifara u 25 koraka, pokušao sam da proverim imali tu istine. Program sam napisao u JavaScript-u i rezultati su sledeći: Broj iteracija 1, rezultat Pi = 3.1333333333333333 Broj iteracija 2, rezultat Pi = 3.1414224664224663 Broj iteracija 3, rezultat Pi = 3.1415873903465816 Broj iteracija 4, rezultat Pi = 3.1415924575674356 Da, autori se izgleda nisu šalili, ovo zaista liči na Pi. Nedostatak programa koji sam testirao je u tome što je sklepetan u par minuta pa verujem da bi mogao da proizvede i bolje rezultate, što prepuštam radoznalima. Nisam to hteo da pominjem u prethodnim postovima, ali kad smo već razvukli diskusiju, za izračunavanje broja Pi postoje i FFT algoritmi. Poznato je da je složenost FFT algoritama reda O( n log(n) ) pa je moguće da su autori članka u Wikipedia, koju @Nedeljko kritikuje, upravo imali na umu takve algoritme. [ Nedeljko @ 17.04.2009. 10:39 ] @
Svi članovi tog reda su pozitivni realni brojevi. Opšti član je
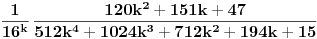 , ,pri čemu k ide od nule. 26-ti član se dobija za k=25 i iznosi preko 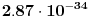 pa je samim tim i ostatak parcijalne sume prvih 25 članova veći od toliko (nije mnogo veći), što znači da je to dovoljno za dobijanje broja pa je samim tim i ostatak parcijalne sume prvih 25 članova veći od toliko (nije mnogo veći), što znači da je to dovoljno za dobijanje broja  sa tačnošću od 33 decimale. sa tačnošću od 33 decimale.Ovaj red u svakoj iteraciji daje malo više od jedne dekadne cifre tačnosti, kao što tvoj račun i pokazuje. Za dobijanje 45000000 decimala ti treba nekih 37 miliona članova ovog reda. Naravno, ova formula se pomoću algoritma binarnog preplitanja Čudnovskog (binary splitting algorithm) za sumiranje konačnih suma može iskoristiti za konstrukciju efikasnog algoritma složenosti 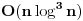 . Tim algoritmom se prvih 37 miliona članova reda sumira u 25 iteracija algoritma binarnog preplitanja Čudnovskog. To je drugo. . Tim algoritmom se prvih 37 miliona članova reda sumira u 25 iteracija algoritma binarnog preplitanja Čudnovskog. To je drugo.http://en.wikipedia.org/wiki/Binary_splitting Svi poznati algoritmi te složenosti koriste ili FFT ili njenog rođaka NTT (Number theoretical transform) za množenje sa složenošću 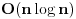 , preko kojeg se realizuju delenje (i po potrebi korenovanje) sa složenošću , preko kojeg se realizuju delenje (i po potrebi korenovanje) sa složenošću 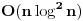 . .Hajde ti lepo šibni tu referencu, pa da vidimo šta tačno piše. Članak nije dovoljno imati, već se mora i razumeti. [ holononi @ 17.04.2009. 13:03 ] @
@Nedeljko
Opet menjaš priču. Tvrdio si da BBP algoritam ne izračunava broj Pi već Citat: na toj formuli zasnovan efikasan algoritam za računanje n-te decimale broja Pi Ipak, izgleda da BBP može oboje. [ Nedeljko @ 18.04.2009. 10:31 ] @
Da, na toj formuli jeste zasnovan efikasan algoritam za heksadekadnih cifara broja
 . Pa, gde sam ja to napisao da se na toj formuli ne može zasnovati algoritam za računanje prvih n cifara tog broja? Naravno, algoritmi koji daju različite izlaze su različiti. . Pa, gde sam ja to napisao da se na toj formuli ne može zasnovati algoritam za računanje prvih n cifara tog broja? Naravno, algoritmi koji daju različite izlaze su različiti.Citat: Nedeljko: taj algoritam nema složenost koju pominješ za računanje prvih n decimala broja  , već je na toj formuli zasnovan efikasan algoritam za računanje n-te decimale broja , već je na toj formuli zasnovan efikasan algoritam za računanje n-te decimale broja  . .Dakle, reč je o složenosti izračunavanja, tj o ovome Citat: holononi: Naprotiv, Bailey, Borwein i Plouffe su konstruisali algoritma za izračunavanje broja Pi vremenske složenosti O( n ) i prostorne složenosti O( ln(n) ). U 25 koraka daje 45 miliona cifara broja Pi. Kad budem imao malo više slobodnog vremena proveriću (ako se dual pentijum ne zapali od tolikog računa). Daleko od toga da postoji ikakav algoritam za bilo šta čija je prostorna složenost manja od prostorne složenosti rezultata ili čija je vremenska složenost manja od prostorne. [ Nedeljko @ 20.04.2009. 18:21 ] @
Evo još jednog propusta na Wikipedia-i: Na stranici o forsingu
http://en.wikipedia.org/wiki/Forcing_(set_theory) nigde se ne pominje uslov cepanja, to jest da od svakog uslova p postoje jači uslovi q,r, koji su nekompatibilni, odnosno takvi da ne postoji uslov s koji je jači i od q i od r. Bez toga (tj. samo iz aksioma parcijalnog uređenja) se ne može dokazati da generički filter ne pripada modelu. Standardan dokaz ne prolaza jer skup 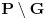 ne mora biti gust, a ima i kontraprimer je bilo koje konačno uređenje ne mora biti gust, a ima i kontraprimer je bilo koje konačno uređenje  i skup i skup 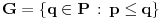 , gde je , gde je  bilo koji minimalni element, G jeste generički filer jer svaki gust skup mora da sadrži p. bilo koji minimalni element, G jeste generički filer jer svaki gust skup mora da sadrži p.Sličan propust je načinjen na stranici o bulovsko-vrednosnim modelima, gde nema uslova bezatomičnosti Bulove algebre. http://en.wikipedia.org/wiki/B...an-valued_models_of_set_theory Pominje se slabiji i nedovoljan uslov da je Bulova algebra beskonačna. Da se razumemo, wikipedija je odlična, ali nije idealna, niti za slapo verovanje, a izgleda i da "doktorati iz polumračnih prostorija" ipak vrede više. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|