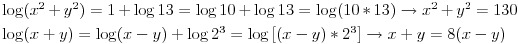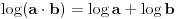|
|
[ vbj @ 10.04.2009. 05:52 ] @
|
| Dugo vec radim ovaj zadatak i nikako da prokljuvim kako bi trebalo da se uradi. Nije mi jasan.
Ja kada radim zanemarujem ove logaritme. Sto posto tu gresim, ali u skoli nikada nisam radio ovako nesto te mi treba vasa pomoc. Hvala. Evo kako izgleda: |
[ igorpet @ 10.04.2009. 08:25 ] @
Logaritmi ti nisu bas jaca strana.
Moj ti je savet da za pocetak dobro naucis osnovna pravila i osobine logaritama.
U ovim jednacinama imao si vrlo jednostavne transformacije posle kojih se oslobadjas logaritama.
Ja cu ti ponovo dati kompletan postupak oslobadjanja od logaritama, iako to mozda nije najbolji put da se nauci ovo.
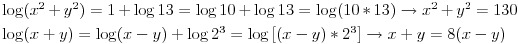
A evo i sta bi trebao da znas u vezi logaritama da bi mogao da resavas ovakve zadatke.
Nema puno pravila i nisu teska za nauciti.
 [ Kolins Balaban @ 10.04.2009. 09:54 ] @
nikad ne zaboravi definiciono podrucje ;) kakvu god jednacinu (sistem jednacina) da radis. kod logaritma numerus mora biti veci od nule.
[ Nedeljko @ 10.04.2009. 10:36 ] @
Tako je. Recimo, formula 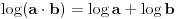 , koja je navedena na ovom skeniranom papiru, nije matematički identitet, jer leva i desna strana jednakosti nemaju isti domen. Leva je definisana kada su brojevi a i b različiti od nule i istog znaka, a desna samo kada su oba pozitivna. Recimo, za a=-2 i b=-3 je leva strana definisana (in ima vrednost log 6), a desna nije. Slično važi i za druge formule sa papira. Fale uslovi pod kojima te formule važe. [ vbj @ 10.04.2009. 14:18 ] @
E, pa, hvala vam braco! Stvarno ste carevi. Moracu da cesce postavljam zadatke na ovaj forum.
[ Kolins Balaban @ 10.04.2009. 15:09 ] @
morat cu te razocarati, jer ti ovdje nece niko rjesavati zadatke. ovo je bio izuzetak, jer se htjelo objasniti kako se treba raditi ovakav tip zadatka, posto si naveo da se s tim nisi sutretao u skoli (iako mi je to malo cudno). nemoj sad da ti dodjes sa jos 15 zadataka iz neke zbirke, i ocekujes da ce ti ih neko ovdje raditi. nadam se da smo ti pomogli i uputili te kako treba da se radi ovakav tip zadatka. nadalje, ako zelis bilo kakvu pomoc, moras da pokazes da si nesh sam radio, pa da nam kazes u kom si koraku zapeo itd itd, a ne samo postavis zadatak i cekas.
[ R A V E N @ 10.04.2009. 15:59 ] @
Uzmi knjigu iz matematike i pročitaj poglavlje o logaritmima - to se radi u 2. razredu srednje škole.Onda uzmi zbirku i kreni sa vježbanjem.Moguće da ćeš tu zaglaviti,jer meni lično je uvijek bio najteži prelaz sa teorije na praksu,zato se nadaj da zbirka ima upute za početne zadatke.
Kasnije ćeš vidjeti da imaju i profesionalnije knjige koje obrađuju tu materiju.
Isto je dobro da nabaviš i onu džepnu knjižicu sa rezimeom i formulama iz matematike i fizike.
[Ovu poruku je menjao R A V E N dana 10.04.2009. u 17:15 GMT+1]
[ vbj @ 10.04.2009. 20:52 ] @
Citat: Kolins Balaban: morat cu te razocarati, jer ti ovdje nece niko rjesavati zadatke. ovo je bio izuzetak, jer se htjelo objasniti kako se treba raditi ovakav tip zadatka, posto si naveo da se s tim nisi sutretao u skoli (iako mi je to malo cudno). nemoj sad da ti dodjes sa jos 15 zadataka iz neke zbirke, i ocekujes da ce ti ih neko ovdje raditi. nadam se da smo ti pomogli i uputili te kako treba da se radi ovakav tip zadatka. nadalje, ako zelis bilo kakvu pomoc, moras da pokazes da si nesh sam radio, pa da nam kazes u kom si koraku zapeo itd itd, a ne samo postavis zadatak i cekas.
Bre Kolins, sta se ljutis? Spremam prijemni i susrecem se sa zadacima koje sam ili u srednjoj radio pa zaboravio ili ih prvi put vidim. Postavljam samo zadatke koje ne mogu da resim ili mi ne ispada isto resenje. Prvo krenem da radim pa tek onda postavim pitanje. [ rajco @ 11.04.2009. 01:03 ] @
Mogu li da te zamolim da nam kazes koji grad i koja je skola u pitanju ako nije problem?
[ Kolins Balaban @ 11.04.2009. 11:07 ] @
ne ljutim se, samo ti pokusavam pomoci. necu ti pomoci ako budem JA rjesavao tvoje zadatke ;) ako te stvari nisi radio, ili si ih zaboravio, najbolje rjesenje je da sjednes, fino pregledas oblasti koje dolaze na prijemnom, zapises na papir sve oblasti i tipove zadataka koje nisi nikad vidio, ili si zaboravio, i platis nekom profesoru da sjedne s tobom, i objasni ti to fino, krenuvsi od teorije (koja je najbitnija) sa ponekim primjerom. nakon toga ti treba da zbavis sto vise testova sa tih prijemnih, i da krenes raditi, pa gdje zapne, tu smo da pomognemo. to sto ti ne znas ni zapoceti zadatak, je upravo radi toga sto ne znas teoriju. na prijemnim ispitima ne dolaze neki preteski zadaci, sa nekim extra fazonima, gdje bas moras ubosti nacin kako doci do rjesenja. vecinom su to tipski zadaci, da se provjeri koliko znas osnovne stvari.
[ Cabo @ 13.04.2009. 11:39 ] @
Citat: Nedeljko: Tako je. Recimo, formula 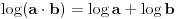 , koja je navedena na ovom skeniranom papiru, nije matematički identitet, jer leva i desna strana jednakosti nemaju isti domen. Leva je definisana kada su brojevi a i b različiti od nule i istog znaka, a desna samo kada su oba pozitivna. Recimo, za a=-2 i b=-3 je leva strana definisana (in ima vrednost log 6), a desna nije. Slično važi i za druge formule sa papira. Fale uslovi pod kojima te formule važe.
Zar ovde ne važi implicitno pravilo da je domen presek domena leve i desne strane, pošto nije eksplicitno naveden domen? [ Nedeljko @ 13.04.2009. 12:13 ] @
Kad se kaže identitet, misli se i da su domeni isti da bi jedan od izraza uvek mogao da zamenjuješ onim drugim u oba smera, a ne da ti se domen suzi ili proširi.
[ Cabo @ 15.04.2009. 10:36 ] @
Citat: Nedeljko: Kad se kaže identitet, misli se i da su domeni isti da bi jedan od izraza uvek mogao da zamenjuješ onim drugim u oba smera, a ne da ti se domen suzi ili proširi.
Odnosno, ako važi jednakost, onda se posmatraju restrikcije leve i desne strane na presek njihovih domena. Inače jednakost ne važi. [ Nedeljko @ 15.04.2009. 11:19 ] @
Možeš reći da jedankost važi u slučaju definisanosti obeju strana, međutim, to se ne zove identitetom, jer log((-2)(-3)), što je definisano, ne možeš da zameniš sa log(-2) + log(-3), jer je nedefinisano. Definicija identiteta je takva zbog njegove primene. Kada piše da je nešto identitet, onda možeš da vršiš zamene u oba smera bez razmišljanja,
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|