Za 1. zadatak je li jedino rjesenje trivijalno rjesenje

Ne. Oba imaju popriličan broj netrivijalnih rešenja.

Evo rešenja prvog zadatka.

Primetimo da je ceo deo leve strane baš prvi sabirak, a razlomljeni deo je drugi sabirak. Dakle, rešenje možemo tražiti izjednačavanjem razlomljenog, odnosno celog dela leve i desne strane zasebno.

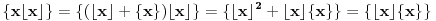
Kako važi , prvi uslov je

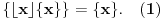
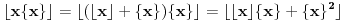
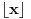
Slično raspisujemo , pa se zahtev da ovo bude jednako može zapisati i kao

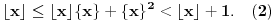
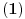
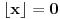
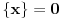
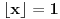
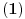
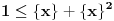
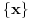
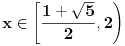
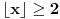
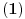
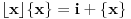
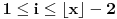
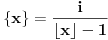
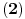
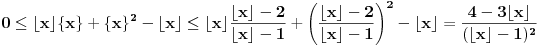
Posmatrajmo sada . Za odatle sledi i , što ostavlja kao jedinu mogućnost, a proverava se da to jeste rešenje. Dalje, za uslov uvek jeste zadovoljen, pa još treba obezbediti (druga strana je uvek ispunjena); rešavanjem ovoga po dobijamo finu kolekciju rešenja, naime . Sledeći slučaj je , kada se svodi na za neko , iz čega dobijamo ; no, iz sada proizlazi da mora važiti , pa ovde nema rešenja. 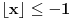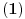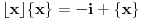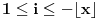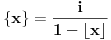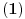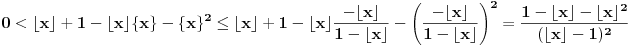Za kraj, ako važi , svodimo na za neko , odakle sledi ; iz dobijamo da mora biti , tj. 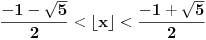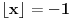, pa je jedino moguće , što daje rešenje .

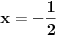
Kad podvučemo crtu, zaključak je: .

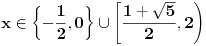
Drugi ostavljam nekom drugog, ali nema razloga da isti postupak ne prođe.

Rešiti jednačinu:



po , .

a) Ako je , jednačina postaje , te je zadovoljena za svako

b) Ako je , stavimo , gde je . Tada jednačina postaje



Za , sabirak pod znakom sume imaće vrednost , a za imaće vrednost . Jednačina stoga postaje



to jest, dobijamo identitet. Prema tome, polazni izraz važi za svaki ceo broj .

Tačno, s tim što ga nigde nisam video ranije. Došao sam samostalno do njega. Ne znam da li ga neko drugi negde video.

Moj dokaz se zasniva na tome da za funkciju važi i za svako .

Zapravo je posredi poseban slučaj Ermitovog (Charles Hermite) identiteta



za racionalno oblika . Ermitov identitet takođe se lako dokazuje sličnom idejom kao gore, ako se stavi , gde je (tj. ako se "stisne" u podinterval dužine )

_{[Ovu poruku je menjao Farenhajt dana 14.04.2009. u 11:26 GMT+1]}

Hvala.

Da li je neko zainteresovan za drugu jednačinu ili da kačim rešenje?

Evo ja ću, kad već neće niko.

Tvrdimo da je rešenje polazne jednačine: .

Ako bi bilo , ostalo bi , pa bi važilo (zapazimo, trebaće nam posle, da važi i obratno: ako , onda je ). No, sada bismo dobili , pa iz date jednačine sledi da je jedino rešenje u ovom slučaju .

Dakle, neka sada bude , tj. . Slično kao u prethodnom zadatku, zasebno ćemo izjednačavati razlomljeni, odnosno ceo deo leve i desne strane. Razlomljeni deo leve strane je , pa je prvi zahtev

Ceo deo leve strane je , pa je idući zahtev

Odmah zapazimo da se leva nejednakost u transformiše u , iz čega izvlačimo da nema rešenja kad god je (jednakost uključujemo jer ). Dakle, ostaje , i se svodi na za neko . Odatle dobijamo . Tvrdimo da ne može biti zadovoljeno za : svodi se na kontradikcija. Dakle, jedina mogućnost je , tj. gde je , a nije teško proveriti da sve ovo jesu rešenja.

Vrlo lepo, sedi, pet

Samo jedna estetsko-simplifikacijska intervencija: tvoje rešenje može se napisati u obliku za , što će zapravo reći za