[ vbj @ 18.04.2009. 00:17 ] @
| Zadatak je ovaj. Resenje u zbirci je x e (1, + oo) Meni ovako ispada: |
|
[ vbj @ 18.04.2009. 00:17 ] @
[ Bojan Basic @ 18.04.2009. 00:28 ] @
[ vbj @ 18.04.2009. 00:32 ] @
Citat: Bojan Basic: Prvo pitanje je kako si od znaka  prešao na prešao na  . A drugo, razmisli bolje kad je razlomak jednak nuli. :) . A drugo, razmisli bolje kad je razlomak jednak nuli. :)Dobro, greska. To cu ispraviti. Ali me zanima da li sam dobro uradio zadatak? [ Bojan Basic @ 18.04.2009. 00:47 ] @
Pošto imaš greške, znači da nisi dobro uradio zadatak. Moraš to ispraviti, pa ćemo videti je li onda dobro.
[ rajco @ 18.04.2009. 00:52 ] @
Druga greska na koju ti je ukazao Bojan spada u osnove matematike, tako da nisi ni blizu.
[ igorpet @ 18.04.2009. 14:00 ] @
Ajd i ja da pripomognem, malo konkretnije:
I Prva stvar kad resavas logaritamske jednacine ili nejednacine je da postavis uslov da je sve ono sto je ispod logaritma bude vece od nule. U konkretno tvom slucaju 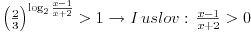 U nekim drugim slucajevima, ako imas vise izraza pod logaritmom svi oni moraju biti veci od nule. npr. 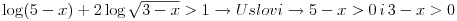 iako ovde ovaj drugi uslov mora da zadovolji i da izraz pod korenom 3-x>=0 mora biti >=0 ali posto je sve to pod logaritmom onda se uzima da je samo >0 II U tvom konkretnom slucaju imamo 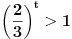 i trebamo da vidimo za koje t vrednosti je leva strana >1 i trebamo da vidimo za koje t vrednosti je leva strana >1-Ako stavimo da je t=0 onda su leva i desna strana jednake, a to nam ne treba -Ako za t uzmemo brojeve koji su veci od nule onda se razlomak 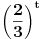 priblizava nuli kako rastu brojevi za t, a to je zato sto su 2/3=0,666... tj broj koji je manji od 1 i kada se takav broj stepenuje bilo kojim drugim pozitivnim brojem on postaje jos manji nego sto je bio.I ovo je ono sto nam ne treba priblizava nuli kako rastu brojevi za t, a to je zato sto su 2/3=0,666... tj broj koji je manji od 1 i kada se takav broj stepenuje bilo kojim drugim pozitivnim brojem on postaje jos manji nego sto je bio.I ovo je ono sto nam ne treba-Ako za t uzmemo brojeve koji su manji od nule onda je razlomak 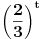 veci od 1. Zato sto veci od 1. Zato sto 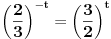 tj. 3/2=1,5 tj. to je broj veci od 1 i kada njega stepenujemo bilo kojim brojem vecim od nule on ce biti veci od jedan. tj. 3/2=1,5 tj. to je broj veci od 1 i kada njega stepenujemo bilo kojim brojem vecim od nule on ce biti veci od jedan.Zato je drugi uslov u ovom slucaju 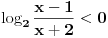 III I treca stvar koju trebamo znati kod resavanja logaritamskih nejednacina: - kada je baza veca od 1 prepisujemo znak nejednakosti jer je funkcija rastuca - kada je baza izmedju 0 i 1 okrecemo znak nejednakosti jer je tada funkcija opadajuca tj. npr. kada je: 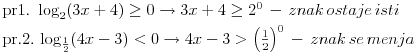 U ovom konkretnom slucaju 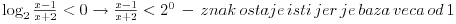 Znaci imas dva uslova: 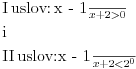 Nadam se da nigde nisam pogresio, jer sam kucao u jednom dahu, ali ovakav je princip rada. A ti sad lepo nastavi dalje i resenje ostavi ovde da bi i ostali videli kako treba da se uradi. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|