[ Farenhajt @ 18.04.2009. 07:02 ] @
|
[ Bojan Basic @ 18.04.2009. 14:34 ] @
Ti se u poslednje vreme baš ozbiljno baviš celim delovima, da ne planiraš možda doktorat na tu temu?
Ne bih sad ništa pisao, samo mislim da bi bilo fino zapaziti sličnost s trećim problemom za treći i četvrti razred srednjoškolskog Saveznog takmičenja 2005. [ Farenhajt @ 18.04.2009. 19:06 ] @
Ma jok, tako se zalomilo
Što se zadatka s takmičenja tiče, jesu slični, a koliko vidim, daju se rešiti i sličnim postupkom. [ Farenhajt @ 20.04.2009. 19:09 ] @
Pošto izgleda ni ovo ne bi zanimalo nikoga sem Bojana, okačiću svoje rešenje:
Očigledno je 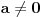 . Stavimo . Stavimo 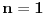 . Tada je . Tada je 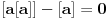 . Odatle sledi da . Odatle sledi da  ne može biti negativno, pošto bi ne može biti negativno, pošto bi 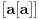 bilo nenegativno (jer bi bilo nenegativno (jer bi 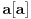 bilo pozitivno), a bilo pozitivno), a 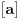 bi bilo negativno, te bi leva strana bila pozitivna. Stoga možemo nastaviti ovako: bi bilo negativno, te bi leva strana bila pozitivna. Stoga možemo nastaviti ovako:(a) 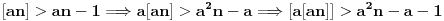 i i 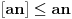 daju daju 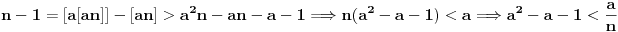 (b) 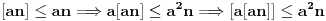 i i 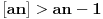 daju daju 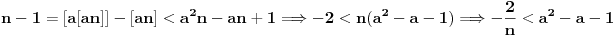 Iz (a) i (b) dobijamo 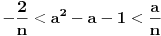 , ali pošto to mora važiti za proizvoljno veliko , ali pošto to mora važiti za proizvoljno veliko  , zaključujemo da je , zaključujemo da je 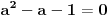 , te uz , te uz 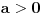 dobijamo dobijamo 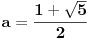 Sada moramo dokazati da identitet važi za 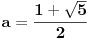 . Ako stavimo . Ako stavimo 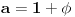 , izraz će se uprostiti u , izraz će se uprostiti u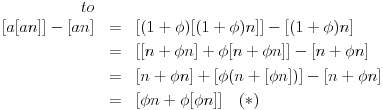 (Napomena: Ne shvatam ovo "to" koje se pojavljuje u gornjem izrazu. Je li to neki bag u LaTeX-u?) Iz 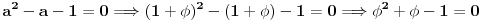 dobijamo dobijamo 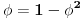 . Ako to uvrstimo u . Ako to uvrstimo u 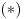 , dobijamo , dobijamo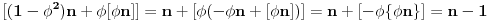 , pošto je , pošto je 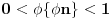 (strogost leve strane poslednje nejednakosti potiče od iracionalnosti broja (strogost leve strane poslednje nejednakosti potiče od iracionalnosti broja  , tj. iz činjenice da navedeni razlomljeni deo nije nula ni za jedno prirodno , tj. iz činjenice da navedeni razlomljeni deo nije nula ni za jedno prirodno  ). ).Prema tome, zaključujemo da je tražena jedinstvena vrednost parametra 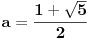 [Ovu poruku je menjao Farenhajt dana 20.04.2009. u 20:30 GMT+1] Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|