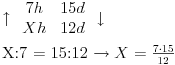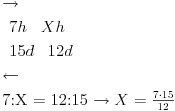Moras nam dati konkretan primer koji ti nije jasan, tvoju verziju istog, pa ce onda neko to podrobnije i objasniti.

Koliko kosta 7kg krompira ako je za 5kg krompira placeno 120 dinara ?
Tu ide ono, obicna proporcionalnost....
X:7=120:5
5X=120*75
x=168 dinara

To znaci ono, najprostiji primer....

E sad ovo mi nije jasno, ja sam dosao do resenja, al da mi neko objasni kako, sta, kad ide ta obrnuta posto sam totalni laik :).

recimo....

Tri moler aokrece stan za cetiri dana. Koliko molera je potrebno da bi isti stan bio okrecen za 3 dana....?
I sad ja sam logicno krenuo da radim kao i prvi, al naravno nije tako :) ?
Aj ako je neko dobre volje nek mi objasni, pa kasnije imam jos pitanja....

Evo nesto ukratko:

Kada pricamo o krompiru i ceni: Sto imamo vise krompira veca je i cena, a vazi i obrnuto sto manje krompira kupimo treba nam manje para, pa je proporcionalnost direktna.

A ako pricamo o molerima i krecenju: Sto vise ljudi kreci jedan stan brze ce ga zavrsiti, tj. sto vise molera - manje vreme i sto imamo manje molera koji krece treba ce vise vremena da zavrse taj isti posao, pa je proporcionalnost obrnuta.

Nema univerzalnog pravila, ali samo razmisljaj logicki da bi odredio da li je proporcionalnost direktna ili obrnuta.

Npr. ako pricamo o zvuku: Sto vise vremena zvuk putuje veci ce put preci - direktna proporc.
Npr. o autu: Sto vise vremena auto vozimo prelazimo vecu kilometrazu - direktna proporc.
Ako pricamo o brzini: Sto se neki auto krece vecom brzinom put ce preci za krace vremena - obrnuta proporc.

Evo da se naslonim na Igora:

Zadatak: Ako je auto prešao određeni put brzinom od 60 km/h za 6 sati, koliko će mu trebati za isti taj put brzinom od 90 km/h?

Naravno, možeš da se "snađeš", pa da prvo izračunaš put, pa ga podeliš novom brzinom, i tako dobiješ rezultat. Ali hajde da ga uradimo obrnutom proporcijom.

Dakle, brzina i vreme su obrnuto proporcionalni (što veća brzina, kraće vreme), a to prosto znači ovo: PRVA brzina prema DRUGOJ brzini isto je što i DRUGO vreme prema PRVOM vremenu (uoči "PRVA-DRUGA" i "DRUGO-PRVO", što i jeste razlog za naziv " obrnuta proporcija").

Dakle, 60 (prva brzina) : 90 (druga brzina) = t (drugo vreme) : 6 (prvo vreme)

60 x 6 = 90t

360 = 90t

t = 4

Sad ti lepo postavi proporciju za taj zadatak s molerima.

_{[Ovu poruku je menjao Farenhajt dana 23.04.2009. u 17:36 GMT+1]}

Ahaaaa.... E ljudi, hvala puno ! :).... Znao sam ja da ovde ima onih koji lepo to objasnjavaju :)
Javljam se ponovo kad mi zapne. Imam mnogo toga ! ;).
Jel ima mozda neko vreme da odvoji, da mi da msn, gmail bilo sta, pa tako da me uputi brze, lakse :)

Pozdrav !

U jednom trenutku mislim da sam shvatio i onda padnem !
Evo recimo ovaj zadatak:

Ako dnevno radi 7 casova, jedan radnik posao zavrsi za 15 dana. Koliko casova dnevno bi radnik trebalo da radi da bi isti posao zavrsio za 12 dana ?

Mozete li nekako da mi objasnite graficki ili sta znam da sto bolje razumem :S
Ovde je takodje obrnuta jel tako ?

Ako hoce da ga zavrsi za 12 dana onda naravno treba u jednom danu da radi veci broj sati.... Al kako sad postaviti proporciju.
Eto pogledao sam da ide
7 : X = 12:15

Al ne razumem.... Prvi put kad sam radio, postavio sam
Sat prema dan= dan prema sat

7:15=X:12
Tako sam ga postavio.... :S Daj pomozite u resavanju mog APSURDNOG problema koji niko ne moze da razume !
zZ

Ajmo recimo prvo ovako da razmotrimo problem: ako neko radi 7h dnevno i posao zavrsi za 15 dana to znaci da je posao zavrsen za 7*15=105h (radnih sati).
Ovo je nadam se potpuno jasno. E sada ako neko hoce da ovih 105h odradi za 12 dana onda mora dnevno da radi 105/12=8,75h sati dnevno, mislim da je ovaj nacin dobar za shvatanje problema.

A ako hocemo proporcijama da ovo resimo, onda radimo vrlo slicno.
Prvo cemo da utvrdimo da je proporcionalnost obrnuta, jer da bi radili manje dana - moramo da imamo vise radnih sata.
Tvoja greska je bila u tome sto si lose potpisao vrednosti. Ide dan ispod dana i sat ispod sata (npr. pises horizontalno a proporciju postavljas gledajuci vertikalno):


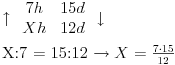
Ili (ako postavis drugacije onda mora i proporcija da se gleda drugacije):

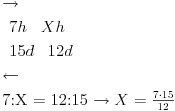
Znaci proporcije uvek postavljas u "pravcu istih jedinica" (sat prema sat, dan prema dan, dinar prema dinar, ...)

Pre svega @Igore hvala ti na trudu koji ulazes u moje ne znanje :D.... Stvarno ti hvala !
Pa mogu da kazem da sam skapirao.... I nekako sam radostan :)...
Kazi mi samo, jel uvek idem ovako... Jel najbolje pri svakoj proporciji ovako poredjati
SAT SAT, DAN DAN, KILO KILO, DINAR DINAR i onda raditi ? To je mislim najpouzdaniji nacin, a onda odrediti dal je direktna ili obrnuta...

Hvala !

Pozdrav !

Upravo tako. Veličine jedne vrste UVEK na jednu stranu, a veličine druge vrste na drugu stranu. I onda paziš da li je direktna ili obrnuta proporcija.

Ako je direktna, ređaš PRVO : DRUGO = PRVO : DRUGO

Ako je obrnuta, ređaš PRVO : DRUGO = DRUGO : PRVO

Hvala i tebi Gorane, stvarno se trudite :) za pohvalu !
Odradicu ujutru jos neke zadatke, pa cu videti dal mi je jasno ! Znaci kao kod jednacina, poznate-nepoznate, a ovamo jedno-drugo...
Skapirao sam ;)

Pozdrav !

p.s. Koliko kosta 7kg krompira ako je za 5kg krompira placeno 120 dinara ? (ajde da ponovo uznem najprostiji primer)

Evo ovo sad da razgranicimo. Rekao si gore u postu
"Upravo tako. Veličine jedne vrste UVEK na jednu stranu, a veličine druge vrste na drugu stranu. I onda paziš da li je direktna ili obrnuta proporcija.".
Onda po tome ispada da treba
kilogram:kilogram=x dinara:120 dinara
umesto:
X:7=120:5
5X=120*75
x=168 dinara

hm.... :S :S


_{[Ovu poruku je menjao Djordjevlasotince dana 25.04.2009. u 03:30 GMT+1]}

Dosadio sam, a ? :(

Ne, nego izgleda da nismo imali primedbi pošto je odgovor tačan.

Ne shvatam šta te muči u zadatku.

Opšta osobina proporcija jeste da unutrašnji članovi smeju da razmene mesta, a smeju i spoljašnji, a da proporcija ostane tačna:

Ako imaš a:b=c:d, onda će važiti i a:c=b:d (unutrašnji su razmenili mesta), a i d:b=c:a (spoljašnji su razmenili mesta).

Usled toga ti dobijaš različit OBLIK proporcije, ali uvek tačan REZULTAT.

Ti si u prvoj poruci postavio X : 7 = 120 : 5, a prema "receptu" dobijaš X : 120 = 7 :5. Uoči da su samo unutrašnji članovi razmenili mesta, dakle sve je u redu.

Prema tome, svaku proporciju možeš postaviti na više načina, i tu je uvek lako zbuniti se. Zato se drži opisanog recepta i biće sve OK

Aham.... Da, da ! Pa provezbao sam jos koji zadatak i mislim da sam ih shvatio ;) ! KAd zapnem oko nekih vise tekstualnih ili nesto javljam se !
PozZ

Rješavanje zadataka pomoću direktnih i obrnutih proporcija je metoda nepotrebno
uvedena u školske programe.Otežava shvatanje suštine, teško se pamti,
lako zaboravlja, doprinosi da se matematika zamrzi, itd.Ko je dobro upamti
kasnije tu metodu koristi i gdje relacije nisu linearne.Naprimjer:
"Kamen pada sa visine od h metara na zemlju za 2 sec.Sa koje visine je pao
kamen ako mu je trebalo 4 sec za to.Ko je dobro ovladao ovom tehnikom proporcija lako će izračunati da je to bilo sa visine od 2*h metara.Nema šanse da
se takvom znalcu dokaže da griješi.

Odbacimo računanje pomoću proporcija.Radimo te zadatke metodom svođenja
na jedinicu.To ide u dva koraka ali je bar kristalno jasno o čemu se radi.
Evo kako to ide:

-7.5 jaja košta 11 dinara.Koliko košta 2.7 jaja?

1)Lijepo izračunamo koliko košta jedno jaje.To je 11/7.5.To zna svako, jel tako?
2)Ako znamo koliko košta jedno jaje lako je izračunati koliko onda košta njih 2.7
komada.I to može svako dijete izračunati, jel tako?

Ili ove proklete "obrnute" proporcije:

-5 volova popase livadu za 8 dana.Za koliko dana će livadu popasti 7 volova?
(E ovo je baš gadan zadatak)

1)Lijepo izračunamo koliko dana treba jednom volu da popase tu livadu.To je
5*8=40 dana (5x više vremena).To zna svako, jel tako?
2)Ako znamo koliko dana treba jednom volu da popase livadu lako je izračunati
za koliko dana će to uraditi njih 7.I to može svako dijete izračunati, jel tako?

Radeći u dva koraka nema šanse da pogriješimo.

Tako ! :). Ne ozbiljno, sad sam napokon shvatio ! Uradio sam 10setak zadataka raznih proporcionalnosti, vrednosti i sve sam po principu po kojem ste objasnjavali (goran u gornjem postu) uradio i sve je tacno JEEE :D
Takodje imam problema sa kvadratnim jednacinama, binomi, trinomi, kvadrat binoma, algebarski izrazi, sve gde je upotrebljen kvadrat i to tako :D. Mnogo mi je tesko da shvatim...

zZ

_{[Ovu poruku je menjao Djordjevlasotince dana 26.04.2009. u 19:38 GMT+1]}

Koliko znam, vi u osnovnoj skoli i ne radite kvadratne jednacine, tj. pojavljuju se samo one koje se mogu resiti po principu ab=0 <=> a=0 v b=0. Daj konkretan primer.

5(X-2)(X+2)-6=(3X-5)^2-(2X+3)^2

(4X-3)^2=(5-4X)^2-16

I slicno....

Ako izvrsis naznacena kvadriranja, zatim sve clanove koji sadrze nepoznatu prebacis na jednu, a sve clanove koji ne sadrze napoznatu na drugu stranu (naravno, kada clan prebacujes sa jedne na drugu stranu, on menja znak), kvadratni clanovi ce nestati i dobices linearnu jednacinu.

5(X-2)(X+2)-6=(3X-5)^2-(2X+3)^2
5(x^2-4)-6=9x^2-30x+25-(4x^2+12x+9)
5x^2-20-6=9x^2-30x+25-4x^2-12x-9
5x^2-26=5x^2-42x+16
5x^2-5x^2+42x=16+26
42x=42
x=1

Dakle, jednacina nije kvadratna....
Slicno se radi i druga jednacina, tj. ni ona nije kvadratna.

moze neko da mi objasni diedar?

http://www.lmgtfy.com/?q=dihedron

http://sr.wikipedia.org/wiki/%D0%94%D0%B8%D0%B5%D0%B4%D0%B0%D1%80



Hedron = hedar, jedar = otprilike površ.

Di+hedron = dijedar = dvo-površ

Poli+hedron = polijedar = više-površ