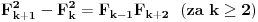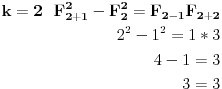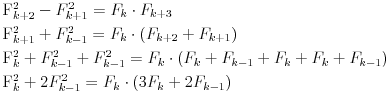Pogledaj http://www.fsb.hr/matematika/download/ZS_fibonaccijev_niz.pdf mislim da ce ti ono sto procitas biti dovoljno da resis zadatak.
A pogledaj i http://mathworld.wolfram.com/FibonacciNumber.html mada mislim da skoro sve imas i u prvom dokumentu.

I pogresno postavljen zadatak.

Prvi clan ima index k+1.

Bazni slucaj:


Kako ovo dokazati za k+1?

Hint:

svedi sve sabirke na indekse k i k-1.

OK. Za k+1:



Evo, k i k-1. Radio sam i dalje od ovoga ali se izgubim, nikako ne mogu da dodjem do dokaza. Jel moze jos neki hint, pa da nastavim dalje?
Hvala

Nisam pratio ovu temu (rekoh bice ono dovoljno), ali ako sada nije kasno evo kako bi ja to: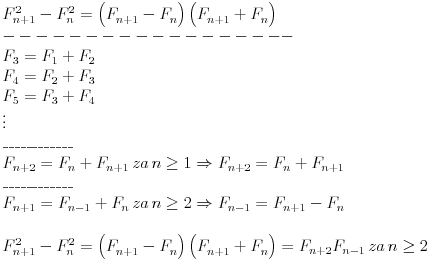


Ako ti treba nesto opsirnije u vezi Fibonacijevih brojeva, javi se na PM, imam finu knjigu (na engleskom)

F(k+1)² - F(k)² =
( F(k+1) - F(k) )( F(k+1) + F(k) ) =
( F(k-1) + F(k) - F(k) )F(k+2) =
F(k-1) F(k+2)