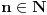
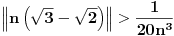
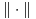
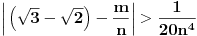
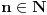
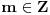
Dokazaćemo malo jače tvrđenje: za svako važi , gde smo sa označili udaljenost od najbližeg celog broja. Pri tom je jasno zašto je ovakvo tvrđenje jače od traženog, a jasno je i da ono odmah sledi ukoliko dokažemo da je za svako i , te ćemo dokazivati ovo poslednje.

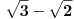
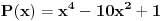
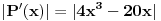
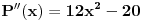
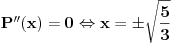
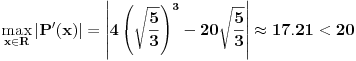
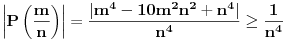
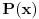
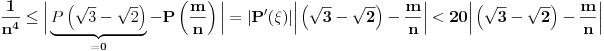
Primetimo da je koren nesvodljivog polinoma . Tražimo maksimalnu vrednost izraza . Kako je , važi , što je potreban, a lako se proverava da je i dovoljan uslov za traženi maksimum, tj. . Dalje, kako je (zbog nesvodljivosti polinoma ), teorema o srednjoj vrednosti nam najzad daje , što smo i želeli dokazati.

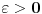
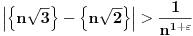
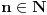
Dodao bih još nešto. Sve ovo nisam smislio ja specijalno za ovu priliku, već je u pitanju imitacija dokaza Lijuvilove (fr. Liouville) teoreme o aproksimaciji. Postoji i slična ali mnogo jača, Routova (engl. Roth) teorema, iz koje sledi da za sve nejednakost važi za svako sem konačno mnogo. Nažalost, nema načina da odredimo koliko može biti izuzetaka, pa smo zato i bili prinuđeni da koristimo slabije, ali konkretnije metode.

auuuuuuuu

LOL