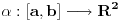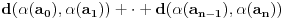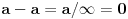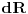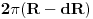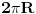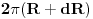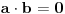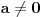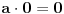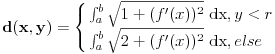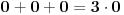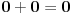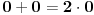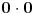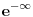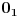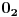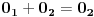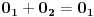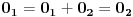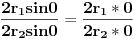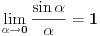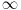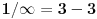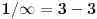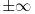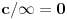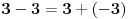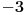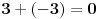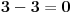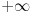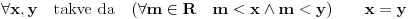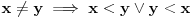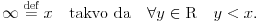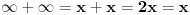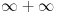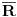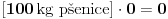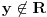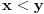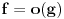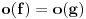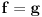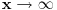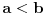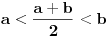|
|
[ galet@world @ 26.04.2009. 07:22 ] @
|
|
Nadam se, pošto je ovo forum za matematiku, da i nematematičari mogu postaviti poneko principijelno pitanje.
Evo šta mene muči:
Ako kružnicu posmatramo iznutra onda je ona konkavna, a ako je posmatramo spolja ona je konveksna što bi
trebalo da znači da je konveksna strana duža od konkavne.
Ako pak smatramo da su obe strane jednako dugačke onda bi dobili pravu jer to je svojstvo prave.
Ako je odgovor da kružnica nema dve strane nego da je to uvek samo jedna strana - odakle onda potiče
zakrivljenost i kako se ona objašnjava kod bilo kakve krive?
Ovo verovatno ne spada u ovu temu pa ako moderator smatra da je interesantno neka ovom nađe neko drugo
mesto. |
[ holononi @ 26.04.2009. 11:32 ] @
Citat: Ako kružnicu posmatramo
Po definiciji kružnica je geometrijsko mesto svih tačaka na rastojanju r (poluprečnik) od date tačke C (centar). U definiciji se ne zahteva sa koje strane se posmatra, da bi bila na kružnici konkretna tačka mora da ispunjava samo uslov rastojanja od tačke C. Kako je dimenzija tačke jednaka 0 (nula) sledi da nema nikakvih dilema u pogledu dužine s jedne ili druge strane.
U opštem slučaju, dužina luka se računa preko integrala. Kad je kružnica u pitanju dovoljno je posmatrati prvi kvadrant. Iz konkavne mogu doći do konveksne funkcije prostom promenom znaka i obratno, a to neće uticati na dužinu.
Krivina krive je mera odstupanja krive od tangente kad se tačka udaljava od dodirne tačke. Jednostavno, poluprečnik krivine je
R = (1+(f'(x))^2)^(3/2) / |f'(x)|
Kod matematičkih pojmova treba se držati definicija dok su intuitivne predstave u drugom planu. Ako se posmatra opna jajeta, onda unutrašnja i spoljnja strana nisu iste dužine. Objašnjenje je jednostavano, broj molekula nije isti sa obe strane. Tada neko može da uzme limenu traku i da je savije u krug i tvrdi da spoljnja i unutrašnja strana nisu iste dužine iako je broj atoma isti. To je tačno, ali savijanjem je povećao medjuatomsko rastojanje na spoljnjoj strani pa ju je produžio. Medjutim i tada treba da bude oprezan jer pri savijanju mogu nastati mikropukotine kod slabo elastičnih materijala a što se može videti mikroskopom.
Skup realnih brojev ima jednu "neobičnu" osobinu. Ma kako uzeli mali interval uvek imamo beskončno mnog tačaka da spojimo dve krajnje tačke neprekidnom linijom. Takvo nešto nema svog analogona u svakodnevnom iskustvu čoveka.
[ galet@world @ 26.04.2009. 16:10 ] @
To što si odgovorio meni je uglavnom poznato, međutim, verovatno me nisi razumeo pa ću pokušati da to objasnim drukčije.
Ako uzmemo pravu liniju onda je međusobni odnos tačaka te linije drukčiji nego međusobni odnos tačaka neke krive linije.
(iako ja smatram da tačke nisu gradivni element intervala, ali to zasad zanemari) Taj odnos je različit i skraćivanje intervala
između krajnjih tačaka ne utiče na tu različitost t. j. zakrivljenost prave i krive su u bilo kojim tačkama različite (izuzev
tačaka infleksije) Dakle sasvim sigurno postoji različitost u odnosu među tačkama - kako je moguće postojanje te
različitosti ako postoje konkavna i konveksna strana krive iste dužine kao što je to slučaj sa stranama prave linije?
Po čemu se onda razlikuju i kako je moguće zakrivljenje ako strane ostaju jednake kao kod prave?
Citat: Skup realnih brojev ima jednu "neobičnu" osobinu. Ma kako uzeli mali interval uvek imamo beskončno mnog tačaka da spojimo dve krajnje tačke neprekidnom linijom. Takvo nešto nema svog analogona u svakodnevnom iskustvu čoveka.
Elementarni element neprekidne linije je interval a ne tačka. Smeštanje tačaka između krajeva intervala ma koliko ih bilo je isto
kao da nismo učinili ništa, a to ima svoj analogon u svakodnevnom iskustvu, ali o tom potom. [ Farenhajt @ 26.04.2009. 21:21 ] @
Citat: galet@world: To što si odgovorio meni je uglavnom poznato, međutim, verovatno me nisi razumeo pa ću pokušati da to objasnim drukčije.
Ako uzmemo pravu liniju onda je međusobni odnos tačaka te linije drukčiji nego međusobni odnos tačaka neke krive linije.
(iako ja smatram da tačke nisu gradivni element intervala, ali to zasad zanemari) Taj odnos je različit i skraćivanje intervala
između krajnjih tačaka ne utiče na tu različitost t. j. zakrivljenost prave i krive su u bilo kojim tačkama različite (izuzev
tačaka infleksije) Dakle sasvim sigurno postoji različitost u odnosu među tačkama - kako je moguće postojanje te
različitosti ako postoje konkavna i konveksna strana krive iste dužine kao što je to slučaj sa stranama prave linije?
Po čemu se onda razlikuju i kako je moguće zakrivljenje ako strane ostaju jednake kao kod prave?
Elementarni element neprekidne linije je interval a ne tačka. Smeštanje tačaka između krajeva intervala ma koliko ih bilo je isto
kao da nismo učinili ništa, a to ima svoj analogon u svakodnevnom iskustvu, ali o tom potom.
Prava je takođe kružnica (beskonačno velikog poluprečnika), te ne postoji nikakva "razlika u međusobnom odnosu" tačaka prave i kružnice. [ galet@world @ 26.04.2009. 23:26 ] @
Citat: Farenhajt: Prava je takođe kružnica (beskonačno velikog poluprečnika), te ne postoji nikakva "razlika u međusobnom odnosu" tačaka prave i kružnice.
Prema ovome sledi da su prava i kružnica beskonačno velikog prečnika identične pojave, ali šta je sa ostalim
kružnicama jer to ne možemo reći za dve kružnice koje imaju različite prečnike odnoso različitu zakrivljenost.
A osim toga po holononiju:
Citat: Po definiciji kružnica je geometrijsko mesto svih tačaka na rastojanju r (poluprečnik) od date tačke C (centar)
po toj definiciji prava ne može biti kružnica jer bi imala dva takva centra t. j. po jedan u svakoj poluravni. [ Farenhajt @ 27.04.2009. 00:11 ] @
Citat: galet@world: Prema ovome sledi da su prava i kružnica beskonačno velikog prečnika identične pojave, ali šta je sa ostalim kružnicama jer to ne možemo reći za dve kružnice koje imaju različite prečnike odnoso različitu zakrivljenost.
ŠTA ne možemo reći?
Citat: galet@world:po toj definiciji prava ne može biti kružnica jer bi imala dva takva centra t. j. po jedan u svakoj poluravni.
Štaviše, svaka prava može pripadati beskonačnom broju ravni, te takvih centara ima beskonačno mnogo, i svi se oni u beskonačnosti poklapaju. Naime, beskonačnost nije "mesto" na koje možeš stati pa reći: "E sad ja odavde imam pregled prave kao kružnice s beskonačno velikim prečnikom." [ holononi @ 27.04.2009. 04:55 ] @
Citat: iako ja smatram da tačke nisu gradivni element intervala Citat: Elementarni element neprekidne linije je interval a ne tačka.
Ma koliko neko nešto smatrao da nije i dalje ostaje da su se matematičari dogovorili da je INTERVAL (otvoren, zatvoren, poluotvoren) SKUP TAČAKA odredjenih osobina. Naravno svi imaju pravo da definišu objekte po volji, ali bih se držao definicija barem dok se ne dogovorimo drugačije. Mada niko ne ume da kaže šta je to tačka.
Takodje, elementarno mi je prihvatljiv stav da je
Citat: Prava je takođe kružnica (beskonačno velikog poluprečnika)
pa je odgovor na postavljeno pitanje upravo konstatacija
Citat: te ne postoji nikakva "razlika u međusobnom odnosu" tačaka prave i kružnice.
bar u kontekstu postavljenog pitanja jer prava je i konveksna i konkavna na skupu realnih brojeva.
f(µx1 + (1-µ)x2) ≤ µf(x1) + (1-µ)f(x2) i kriva je konveksna. Za pravu treba staviti znak jednakosti. I ovo nikako ne utiče na dužinu. Jer dve konveksne krive koje se seku u dve tačke (izmedju kojih analiziramo krive) ne moraju da imaju istu dužinu (izmedju te dve tačke). Na istom intervalu mogu imati jednu konveksnu i jednu konkavnu krivu iste dužine. Iz svega toga mogu da zaključim da su konveksnost i konkavnost irelevantni za dužinu krive.
Citat: kako je moguće zakrivljenje ako strane ostaju jednake
Očekuješ da se spoljnja strana produži jer to sledi iz svakodnevnog iskustva. Ovde jednostavno treba preći sa konkretnog na apstraktno razmišljanje. Tačka nema dimenzije a kriva (prava) linija nema debljinu.
[ galet@world @ 27.04.2009. 07:34 ] @
Za kružnicu konačnog prečnika i pravu, kao i za dve kružnice različitih prečnika ne možemo reći ovo:
Prava je takođe kružnica (beskonačno velikog poluprečnika), te ne postoji nikakva "razlika u međusobnom odnosu" tačaka prave i kružnice.
jer ako ovo uvažimo onda je ovde kružnica upoređena sama sa sobom ili sebi jednakom pa se ovaj iskaz
podrazumeva ali ne kazuje ništa.
Citat: Farenhajt: Štaviše, svaka prava može pripadati beskonačnom broju ravni, te takvih centara ima beskonačno mnogo, i svi se oni u beskonačnosti poklapaju.
Koje je ovde značenje reči "poklapaju"? Ako se svi centri poklapaju onda sve ravni prolaze kroz to mesto
pa ih ne može biti beskonačan broj već samo jedna, zar ne?
Osim toga to bi bila jedina kružnica koja se nalazi u beskonačnom broju ravni i sa problematičnim brojem
centara pa je odstupanje od definicije kružnice očigledno.
Citat: holononi: Mada niko ne ume da kaže šta je to tačka.
Tačku smo mi izmislili i rekli da nema dimenziju. Interval ima jednu dimenziju i po tome je interval pojava sama
za sebe i drukčija od tačke - tačka i interval su dve različite pojave i ne mogu se definisati jedna pomoću druge.
Jednako besmisleno je reći da beskonačan broj tačaka čini neki interval kao kad bismo rekli da beskonačan broj
tačaka čini neki ugao. Tačka, interval i ugao su tri različite stvari.
Citat: pa je odgovor na postavljeno pitanje upravo konstatacija:"...te ne postoji nikakva "razlika u međusobnom
odnosu" tačaka prave i kružnice".
Već sam rekao da ova konstatacija ne kaže ništa jer ne upoređuje pravu sa kružnicom konačnog prečnika.
Citat: ...prava je i konveksna i konkavna na skupu realnih brojeva.
Nije reč o pravoj
Citat: Očekuješ da se spoljnja strana produži jer to sledi iz svakodnevnog iskustva.
I očekujem i ne očekujem - ustvari čekam informaciju o tome - kako se to tumači jer je sasvim sigurno da su
odnosi među tačkama raznih krivih različiti, a ipak ispada da su dužine konkavne i konveksne strane jednake. [ Nedeljko @ 27.04.2009. 07:44 ] @
Ako je 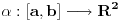 neprekidno preslikavanje, dužina luka  se definiše kao supremum svih realnih brojeva oblika 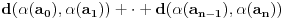 ,  . To je definicija i tu nema nikakvog razmatranja ove i one strane krive. Taj supremum može biti i beskonačan.
Ja mislim da razumem postavljača teme - za bojenje unutrašnje strane papirnatog kružnog cilindra treba malo manje boje nego za bojenje spoljašnje strane istog cilindra. To je zato što taj fizički model ne odgovara u potpunosti matematičkom kružnom cilindru iz dva razloga - papir ima debljinu i sloj boje ima debljinu.
No, matematički stavovi su tačni u kontekstu u kome su formulisani, a taj kontekst je dat definicijama. U standardnom zasnivanju realnih brojeva nema beskonačno malih veličina, pa samim tim ni mogućnosti za uvođenje definicije kojom bi se razlikovao unutrašnji i spoljašnji obim kružnice (a da on bude realan broj). Ako neko time nije zadovoljan, onda treba da kaže šta su tačno njegovi ciljevi, potrebe itd., pa da se nađe neki drugi formalizam koji bi zadovoljio te potrebe. U svakom slučaju, smatram da je motivacija vrlo važna, tj. da uvođenje pojmova bez konkretne motivacije nema mnogo smisla. [ galet@world @ 27.04.2009. 12:51 ] @
Pade mi napamet sledeći "eksperiment":
Ako iz ravni po nekoj kružnici isečemo i izvadimo krug šta dobijamo:
1. rupu ograničenu kružnicom
2. krug ograničen kružnicom
Dakle imamo dve kružnice. Kako da vratimo krug u ravan?
1. Ako su kružnice jednake onda se tačke kružnica poklapaju, zar ne?
2. Ako se tačke kružnica ne poklapaju onda kružnice nisu jednake.
Tačke kružnica se ne poklapaju jer je presecajuća kružnica bila između njih.
Ovo mi liči na paradoks koji je možda već neko pre mene postavio.
[ miki069 @ 27.04.2009. 13:09 ] @
Zar nije iznutra gledano konveksna a spolja gledano konkavna.
[ Nedeljko @ 27.04.2009. 13:53 ] @
galet@world
A zašto jednom ne bi naučio realne brojeve za promenu, jer očigledno postavljaš stalno ista pitanja koja se tiču zasnivanja realnih brojeva.
[ holononi @ 27.04.2009. 14:41 ] @
Mislim da ono što navodi @Nedeljko u prvom postu otprilike stavlja tačku na diskusiju po ovoj temi. Jer i @Nedeljko primećuje da @galet@world na mala vrata uvodi "debljinu" linije, samo što sam ja u prvom odgovoru koristio paralelu sa opnom jajeta i limenom trakom a @Nedeljko papirom.
Citat: tačka i interval su dve različite pojave i ne mogu se definisati jedna pomoću druge.
Ovi stavovi se mogu proveritii u uvodu u (matematičku) analizu. Drugo, ako se pojmovi tačka, prava i ravan posmatraju u smislu Hilbertovih ili nekih drugih definicija treba obrazložiti kako iz toga sledi da su konveksna i konkavna strana kružnice različite dužine.
Citat: kao kad bismo rekli da beskonačan broj tačaka čini neki ugao
Da, ugao se može definisati kao skup tačaka i to konveksan. ALI MERNI BROJ UGLA JE NEŠTO DRUGO. Čak i ako uvedemo strožiju definiciju ugla, služeći se terminima klasa ekvivalencije, to i dalje ostaju samo definicije u datom kontekstu.
Citat: Ovo mi liči na paradoks koji je možda već neko pre mene postavio.
Aksiomatika realnih brojeva i teorije mere ponekad deluju paradoksalno. Da li su površine kruga sa i bez tačaka kružnice jednake?
Na kraju da napomenem jedan primer. Uvek možemo u polju karakteristike 2 konstruisati pravu koja je u stvari kružnica.
[Ovu poruku je menjao holononi dana 27.04.2009. u 20:24 GMT+1][ galet@world @ 27.04.2009. 16:53 ] @
Citat: Nedeljko:
A zašto jednom ne bi naučio realne brojeve za promenu, jer očigledno postavljaš stalno ista pitanja koja se tiču zasnivanja realnih brojeva.
A šta da naučim - da je tačka gradivni element intervala, da funkcija postoji i kad nema argumenta, da je 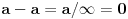 i slične
gluposti koje lansiraju "učeni"?
U nemogućnosti da odgovorite na ovo:
Citat:
1. Ako su kružnice jednake onda se tačke kružnica poklapaju, zar ne?
2. Ako se tačke kružnica ne poklapaju onda kružnice nisu jednake.
Tačke kružnica se ne poklapaju jer je presecajuća kružnica bila između njih.
počeli ste da mi se obraćate lično sa preporukom o obrazovanju koja nema osnov jer vi ste tu
obrazovani pa ipak nemate odgovor. Ovim i ja stavljam tačku na ovu temu jer je jasno da, osim
uvredljivog, pravi odgovor neću dobiti.
[ Farenhajt @ 27.04.2009. 21:02 ] @
Galet@world, reklo bi se, ima problem s činjenicom da tzv. realni brojevi ne postoje u stvarnosti, te da stvarnosno iskustvo veze nema s onim kako su realni brojevi definisani.
Ali pazi sad ovo: SVI brojevi (pa i prirodni) jesu APSTRAKCIJA. Broj, kao pojam, ne postoji u prirodi. On je isključivo misaoni plod ljudskog uma, a pojavio se na osnovu dva temelja: apstrahovanja, tj. zamene jednog objekta drugim (ovca se predstavlja reckom na prutu), i bijekcije (svakoj recki odgovara tačno jedna ovca i svakoj ovci odgovara tačno jedna recka). Stoga bi se moglo reći da su prirodni brojevi svojevrsne klase ekvivalencije diskretnih skupova.
Onog momenta kad su ljudi ustanovili da raznim stvarnim skupovima mogu odgovarati jedni te isti sistemi recaka na prutu, tog momenta se otvorio prostor za pojavu APSTRAKTNOG pojma prirodnog broja. A ako je temeljna vrsta broja, iz koje su se razvile sve ostale, apstraktna, onda su neizbežno takve i sve ostale.
A ako su apstraktne, onda su i sve definicije vezane za njih apstraktne i potpuno je besmisleno tražiti ikakvo njihovo utemeljenje u prirodi. Zato ti savetujem da pronađeš neku drugu, plodotvorniju temu, jer je ova diskusija otprilike na nivou "Zašto su latinična i ćirilična slova baš takva kakva jesu? Zašto su grčka, feničanska bila takva kakva jesu?" Eto, takva su kakva su (može se pratiti njihova grafička evolucija, ali se prvobitni oblik ne može objasniti), i nema tu priče.
[ Nedeljko @ 27.04.2009. 21:04 ] @
Za početak da naučiš zasnivanje realnih brojeva (kompletno uređeno polje), a potom i dužinu luka. Onda nećeš ni postavljati ovakva pitanja, jer će ti stvari koje te muče biti jasne, a ako i ne budu, drugi će ti ih moći objasniti u par rečenica. Dotle ti ni drugi ne mogu pomoći da shvatiš. No, izbor je tvoj.
[ Nedeljko @ 28.04.2009. 08:01 ] @
Da se nadovežem na Farenhajta.
Matematika ne tvrdi da će zrela kruška da padne ko zrela kruška, već da su neki stavovi posledice nekih aksioma. To znači da u bilo kakvom modelu, koliko god on bio "veštački", čudan itd., u kome važe sve aksiome, nužno važe i sve posledice tih aksioma i na taj način se matematika primenjuje. Broj 5 ne mora biti apstraktan. Možemo i drvo pored naše kuće smatrati realizacijom broja 5. Bitno je da na nekom skupu objekata (stvarnih ili misaonih) ispostavimo operacije i relacije tako da budu zadovoljene sve aksiome na primer Peanove aritmetike i onda će u tom modelu (tj. interpretaciji polaznih pojmova) nužno važiti i sve teoreme Peanove aritmetike.
Primera radi, programeri ne mogu da primenjuju formule iz matematike koje se odnose na realne brojeve direktno i neoprezno, jer računarska realizacija realnih brojeva ne odgovara u potpunosti tom matematičkom pojmu (nisu zadovoljene aksiome u punom smislu), već moraju voditi računa o specifičnostima računarske realne aritmetike.
Drugo, što sam već pomenuo, matematički stavovi važe u kontekstu u kome su formulisani, a koji je određen definicijama. Doke ne budeš naučio te definicije, nećeš razumeti ni kontekst tih stvavova, pa će te mučiti ovakve stvari.
[ galet@world @ 29.04.2009. 07:20 ] @
Citat: galet@world: U nemogućnosti da odgovorite na ovo:
1. Ako su kružnice jednake onda se tačke kružnica poklapaju, zar ne?
2. Ako se tačke kružnica ne poklapaju onda kružnice nisu jednake.
Tačke kružnica se ne poklapaju jer je presecajuća kružnica bila između njih.
počeli ste da mi se obraćate lično sa preporukom o obrazovanju koja nema osnov jer vi ste tu
obrazovani pa ipak nemate odgovor. [ Nedeljko @ 29.04.2009. 07:55 ] @
Hajde da se više ne igramo žmurke. Ti ova pitanja nisi postavio da bi ti neko nešto objasnio, već da bi ti drugima objasnio neke stvari. Zato i odbijaš da pročitaš ono što ti se preporučuje i doživljavaš to lično.
Evo, obećavam da ću ti lično ja odgovoriti na sva pitanja iz ove teme čim naučiš kopmpletno uređeno polje (zasnivanje realnih brojeva). Dotle možeš da očekuješ svu pomoć u vezi savladavanja kompletnog uređenog polja. Bez toga ovakve diskusije nemaju nikakvog smisla.
[ Nedeljko @ 29.04.2009. 07:59 ] @
Da dodam. Treba savladati i pojmove supremuma, infimuma i limesa. I tu možeš očekivati svu pomoć, pa kad to savladaš, dobićeš i odgovore na sva pitanja iz ove teme. Verovatno ćeš ih onda znati i sam, ali eto, daću ih ja ako ih budeš tražio.
[ holononi @ 29.04.2009. 09:40 ] @
Citat: vi ste tu obrazovani pa ipak nemate odgovor.
Šta je ovde konkretno pitanje? U citiranom postu su navedene samo rekapitulacije nekih stavova. Ne možemo diskutovati na taj način da ignorišemo opšte prihvaćene principe i definicije. Jer način definisanja pojmova ima posledice na izvedene zaključke. Ukoliko neko pokušva da uvede novu definiciju tu ima odredjene slobode ali mora biti eksplicitan. Denicija kružnice kako sam uveo u postu od 26.04.2009. nije moja izmišljotina već jedna od jednostavnijih poznatih definicija. Isto tako, aksiomatika realnih brojeva se razvija stotinama godina pre nas i nastaviće da se razvija i posle nas.
Odgovor na (prvobitno postavljeno) pitanje leži u činjenici da sve tačke koje ne zadovoljavaju definiciju kružnice ne pripadaju kružnici, bez obzira da li je duža ova ili ona strana. Lično ovde primećujem dva problema,
- Prvi je već pomenuta "debljina" krive;
- Drugi je nemogućnost definisanja konveksnosti i konkavnosti u odnosu na jednu tačku. Sama definicija konveksnosti (bilo kakve funkcije ili skupa) podrazumeva postojanje bar dve tačke (skup od jedne tačke je uvek konveksan). Problem je što pri odredjivanju konveksnosti funkcije razmatramo i tačke koje uopšte ne pripadaju funkciji. Tu leži opasnot da se "izgubimo" u beskonačno malim ili beskonačno velikim veličinama.
Zato, pod strogim držanjem pri navedenim definicijama, nema diskusije sa koje strana je KRUŽNICA duža, KONKRETNA KRUŽNICA JE UVEK ISTE DUŽINE (OBIMA). Medjutim ako neko hoće da kaže da TAČKE koje se nalaze sa konveksne strane neke krive opisuju kraću putanju od tačaka koje se nalaze sa konkavne strane onda je takav zaključak ispravan. Ali tada te tačke ne pripadaju krivoj.
[ Nedeljko @ 29.04.2009. 10:45 ] @
Citat: holononi: Ali tada te tačke ne pripadaju krivoj.
To jest, na pozitivnom su rastojanju od kružnice. To što olovka ima debljinu, pa možemo crtati susedne tačke na papiru, ne važi za realne brojeve, ali ti to naravno z6naš. [ djoka_l @ 29.04.2009. 12:45 ] @
Obično preskačem teme u kojim vidim da galet diskutuje, ali me zanima objašnjenje njegovog "misaonog" primera.
Voleo bih da bi gospodin galet objasni kako iseca krug iz ravni "misaonim" makazama.
1. Tačku koja pripada kružnici ostavlja u ravni
2. Taču koju pripada kružnici ostavlja na odsečku
3. "misaonim" i izuzetno oštrim makazama preseca tačku na pola
Ah da, još jedno pitanje za galeta: koliko je rastojanje između dva "susedna" realna broja
[ holononi @ 29.04.2009. 13:21 ] @
Rastojanje ovde definišemo kao realan nenegativan broj (ajd' da pomenemo i uslove nenegativnosti, normiranosti i σ-aditivnosti kao najosnovnije). Kako je već u ovom forumu uvedeno rastojanje preko supremuma, nema potrebe da se pozivam na definiciju dužine luka preko aproksimirajućih poligona i slično. Podsetiću samo da se dužina luka može izračunati i formulom koju znaju studenti prve godine ne samo matematike već svih tehničkih fakulteta (hmmm... o ovome smo već diskutovali). Ta formula sadrži kvadriran izvod funkcije, te nema značaja da li je funkcija konveksna ili konkavna, promenom znaka menja se i konveksnost/konkavnost, ali nakon kvadriranja opet se dobije ISTI nenegativan broj. Uvodjenjem metrike preko neke norme, na primer 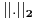 , opet dobijamo iste nenegativne vrednosti bez obzira na konveksnost/konkavnost funkcije. Nema uticja ako krivu damo u parametarskom obliku, opet dobijamo iste nenegativne brojeve.
[ Nedeljko @ 29.04.2009. 13:55 ] @
Citat: djoka_l: Obično preskačem teme u kojim vidim da galet diskutuje
Mnogo propuštaš.
Citat: djoka_l: Ah da, još jedno pitanje za galeta: koliko je rastojanje između dva "susedna" realna broja
Da, koliko je rastojanje između tačke na krivoj sa unutrašnje strane krive i tačke na krivoj sa spoljašnje strane krive?
[ holononi @ 29.04.2009. 14:18 ] @
Citat: koliko je rastojanje između dva "susedna" realna broja
Da vidimo prvo definiciju toga što si stavio pod znake navoda.
[ djoka_l @ 29.04.2009. 14:53 ] @
Pa "susednost" dva realna polja nema smisla (kao i cela ova tema), zato sam i stavio pod znake navoda.
Ako treba definisati ovu besmislenost, uvedimo oznaku da je 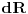 rastojanje dva "susedna" realna broja.
Tada, isto tako besmisleno, možemo reći da je dužina "unutrašnjosti" kružnice 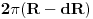 , kružnice 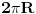 , a "spoljašnjosti" 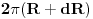 [ galet@world @ 29.04.2009. 19:00 ] @
Ajde da dam moje rešenje
Kružnica oko kruga ima obim 2rpi, a kružnica oko rupe ima obim 2(r+0)pi t. j. 2rpi + 2•0•pi
Smatram da je nula u matematici dosta zapostavljen broj - čak smatram da je nula beskonačan skup
brojeva i da, na primer, nije u redu pisati 2•0 = 0 nego samo kao 2•0
Ako se dve ravni presecaju onda samo tačke na preseku pripadaju obema ravnima - ostale tačke ma
kako bile bliske ne pripadaju obema ravnima - između tih tačaka postoji uvek razmak odnosno interval
i on se nikada ne gubi ni u konačnom ni u beskonačno malom t. j. on postoji i ima dimenziju dužine uvek
dok god te tačke ne padnu u jednu.
Prema tome gornja nula je interval koji ima dimenziju dužine.
Molim da uzmete u obzir da nisam matematičar, a ni mnogi koji ovo čitaju, kao i da zdravorazumski
razmislite o ovom i saopštite razumljivim jezikom prigovor ovom mom razmišljanju, ako je to moguće, a ako
nije onda nikom ništa jer ja, a verovatno i neki drugi članovi i gosti ne nameravamo da zbog ovog proučavamo
matematiku na način kao ljudi koji su se opredelili za to.
[ holononi @ 29.04.2009. 20:04 ] @
Kad govorimo o krugu treba imati na umu
x² + y² < r² (otvoren krug, bez tačaka kružnice)
x² + y² ≤ r² (zatvoren krug, uključuje i tačke kružnice)
x² + y² = r² (kružnica)
U jednom od ranijih postova već sam postavio pitanje ovih površina imajući u vidu upravo ovakvo razmišljanje o kome govoriš. Kad je u pitanju obim kružnice može se pisati nešto ovako
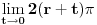
Citat: nije u redu pisati 2•0 = 0 nego samo kao 2•0
Ima aksiom koji kaže svako x iz R, x∙0=0.
Citat: ostale tačke ma kako bile bliske ne pripadaju obema ravnima
Da, to je tačno.
Citat: razmak odnosno intervali on se nikada ne gubi ni u konačnom ni u beskonačno malom
Zato uvodimo limes, kao "mekani prelaz" izmedju dve tačke. Medjutim nemoj zaboraviti problem cilja i strele. Ma koliko meta odmiče, strela je stiže bez obzira što u svakom posmatranom trenutku prelazi samo deo puta. Tu je "prevara" u vremenu, jer onaj ko navodi ovakav primer kao argument, zaboravlja da kad podeli dužinu da mora korigovati i vreme. Jer, opet po definiciji, predjen put je proizvod brzine i vremena, te ne zavisi samo od puta koje prelaze strela i meta.
Citat: Prema tome gornja nula je interval koji ima dimenziju dužine.
E ovo je sada zavrzlama. Može da bude i tačno i netačno. Ako govorimo u smislu datih definicija u ranijim postovima, da tu je dužina nula.
[ galet@world @ 29.04.2009. 21:19 ] @
@holononi
Zahvaljujem! Tako se to radi. Pa da nastavimo dok se može.
Citat: Ima aksiom koji kaže svako x iz R, x∙0=0.
S ovim aksiomom se ne slažem jer ne uzima u obzir "prirodu" nule.
Suprotstavljam mu ovakav moj aksiom:
Neki broj jednakih veličina veći je od jedne takve veličine toliko puta koliki je taj broj ma kakve bile te veličine.
Citat: Medjutim nemoj zaboraviti problem cilja i strele.
Ili, na primer Ahil i kornjača - ovo su dobri primeri gde postoji limes, ali i gde se on postiže.
Dok god strela ne pogodi cilj ili dok god Ahil ne stigne kornjaču postoji interval, ali kad se to
postigne stvar se odjednom skokovito menja i nije više ono što je bila. Pre postizanja limesa
uvek postoji nterval i ništa drugo.
Citat: Ako govorimo u smislu datih definicija u ranijim postovima, da tu je dužina nula.
S ovim se u potpunosti slažem i pravim suštinsku razliku između ovih iskaza:
- tu je dužina nula i
- tu nema dužine
Naravno, interesuje me tvoje mišljenje o ovom.
[ holononi @ 29.04.2009. 21:39 ] @
Citat: S ovim aksiomom se ne slažem jer ne uzima u obzir "prirodu" nule.
Ukoliko se ne slažeš sa tim aksiomom onda rešenje problema moraš tražiti van matematike. Jer na temelju raznih takvih aksiomima je zasnovana matematika kakvu je danas poznajemo. Povremeno se dodaju novi i ulepšaju postojeći aksiomi ali i to se radi na osnovu precizno definisanih stavova.
[ Farenhajt @ 29.04.2009. 23:45 ] @
Citat: galet@world: @holononi
Neki broj jednakih veličina veći je od jedne takve veličine toliko puta koliki je taj broj ma kakve bile te veličine.
Uuuu, voleću da vidim ovaj "zdravorazumski" pristup našeg "zdravorazumskog" kritičara:
Osoba A: Hej, ja tebi triput nisam pozajmio ništa. Nameravaš li ti to da vratiš?
Osoba B: Auuu, druže, znam, imam te na umu, ali zezaju me s platom, evo strpi se samo još nedelju dana, i četiri puta ti neću vratiti ništa, red je da se okamatiš.
Aksiomatika do bola. [ mokelet @ 30.04.2009. 00:01 ] @
Citat: galet@world:
Suprotstavljam mu ovakav moj aksiom:
Neki broj jednakih veličina veći je od jedne takve veličine toliko puta koliki je taj broj ma kakve bile te veličine.
Da bi ti neko odgovorio na ovo "pitanje", moraš prvo da definišeš sledeće pojmove: broj, jednakost, veličina, veće, "toliko puta". [ galet@world @ 30.04.2009. 07:12 ] @
Citat: Farenhajt: Uuuu, voleću da vidim ovaj "zdravorazumski" pristup našeg "zdravorazumskog" kritičara:
Ja nisam vaš kritičar ali zahvaljujem na "dobronamernoj" kritici i korigovaću svoj aksiom tako da glasi:
Neki broj jednakih veličina sadrži jednu takvu veličinu toliko puta koliki je taj broj ma kakve bile te veličine.
Ovim nisam eliminisao kritiku, međutim, da je holononi izneo svoje mišljenje na ovo:
Citat: galet@world:
S ovim se u potpunosti slažem i pravim suštinsku razliku između ovih iskaza:
1 - tu je dužina nula i
2 - tu nema dužine
verujem da bi bilo bi jasno da obaveza koju ima osoba B prema osobi A nema dimenziju duga jer taj primer ne
govori o vrednosti pozajmice već o nepostojanju pozajmice kao što po iskazu 2 nema dužine.
(emotivni izlivi poput "Uuuu" i "... do bola" nisu ovde potrebni )
Citat: mokelet: Da bi ti neko odgovorio na ovo "pitanje", moraš prvo da definišeš sledeće pojmove: broj, jednakost, veličina, veće, "toliko puta".
Slažem se, ali verujem da znaš šta sam hteo da kažem, a pomoć u tom pogledu mi je neophoda i svakako bi dobrodošla. [ Fitopatolog @ 30.04.2009. 07:26 ] @
Citat: galet@world: Neki broj jednakih veličina sadrži jednu takvu veličinu toliko puta koliki je taj broj ma kakve bile te veličine.
Dobro, recimo da to znači da su "veličine" (beskonačno male ili beskonačno velike) uporedive (npr. broj celih i broj racionalnih brojeva). Šta sa veličinama koje nisu uporedive? Npr. broj celih i broj realnih brojeva? Da li dozvoljavaš da tačka pripada grupi veličina koje imaju dimenzije beskonačno puta manje od prve sledeće grupe veličina do nje (ako sortiramo veličine po dimenzijama). I, sada da se malo našalim, iz skupa ovih tačaka izuzimam centar kružnice koji mora biti malo veći da u njega može da se zabode šestar. [ Nedeljko @ 30.04.2009. 08:01 ] @
Citat: galet@world: Neki broj jednakih veličina sadrži jednu takvu veličinu toliko puta koliki je taj broj ma kakve bile te veličine.
Naravno da je 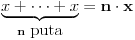 za svako  , pa i za nulu, ali to i dalje ne znači da nije 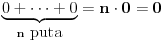 . [ djoka_l @ 30.04.2009. 08:25 ] @
Citat: Smatram da je nula u matematici dosta zapostavljen broj - čak smatram da je nula beskonačan skup
brojeva i da, na primer, nije u redu pisati 2•0 = 0 nego samo kao 2•0
Ja smatram da je 1 prilično zapostavljen broj u matematici - čak smatram da je jedan beskonačan skup
brojeva i da, na primer, nije u redu pisati 2•1 = 2 nego samo kao 2•1 [ holononi @ 30.04.2009. 09:02 ] @
Citat: da je holononi izneo svoje mišljenje na ovo
Stav po ovom pitanju je iznet, ali ponoviću. Ako se ignorišu aksiomi realnih brojeva, tada odgovor treba tražiti u nekoj drugoj disciplini a ne u matematici koja je zasnovana aksiomatski. Stanje materijalnog sveta se čoveku javlja kao dato i zato se u prirodnim naukama ne polazi od aksioma već dogadjanja i eksperimenta. Eksperimentišući, primetićete da se d-linija natrijumovog spektra nalazi na odredjenoj talasnoj dužini vidljive svetlosti pa ćete zaključiti da je energija elektrona tolika i tolika. Usavršavanjem uredjaja ćete primetiti da se ista d-linija cepa na dve veoma bliske, male razlike u talasnim dužinama, pa ćete tražiti objašnjanje u postojanju spina elektrona. Ali za sada ne možete aksiomatski utemeljiti šta će se desiti kad dalje usavršite uredjaje jer to i neznate.
Kako god zasnovali aksiome u matematici, vaše prebrojavanje istih ovaca neće povećati količinu mleka, samo ćete imati predstavu o broju ovaca pa matematički aksiomi mogu da budu zasnovani kao potpuno veštačka kategorija. Vi možete Zemlju postaviti u centar svemira i dobiti tačne jednačine koje opisuju kretanje nebeskih tela. Ali to neće sprečiti sunce da kroz 5-6 milijardi godina proguta svoju decu.
Naravno, svi mogu da sastave svoje aksiome i da krenu s njima u svet. Ali kako je autor ovog posta ubogih intelektualnih mogućnosti, te mora da "bleba" 10-20 sati dnevno / 365 dana godišnje, da bi kako tako procenio kada da upotrebi definiciju dužine kao integral a kada da se pozove na topologiju, onda je odustao od konstruisanja sopstvenog sistema aksioma.
Matematika nije kao ostale discipline pogodna za "udobno" ćaskanje i eksperimentisanje sa žabljim batacima u opuštenoj atmosferi. Bukvalno, svako slovo se meri i odredjuje mu se značaj i uloga. A žablje batake uvek možete, kad vam sve dosadi, propeći i napraviti sendvič, pa ko voli...
PS
Sramota me je što sam u osnovnoj školi eksperimentisao žabama. Tako su nas učili na časovima biologije. Kasnije sam shvatio da tu nema ništa zabavno.
[ japan @ 30.04.2009. 09:06 ] @
Citat: galet@world: smatram da je nula beskonačan skup
brojeva i da, na primer, nije u redu pisati 2•0 = 0 nego samo kao 2•0
galet, ovo što ti pricaš nije besmisleno, naprotiv, vrlo je smisleno, čak je i obrađeno u algebri, a ima veze sa deliteljima nule - za broj  kažemo da je delitelj nule ako je za bar jedno 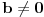 , 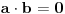 , i kažemo da je pravi delitelj nule ako je pri tome i 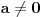 .
međutim, polje realnih brojeva nema pravih delitelja nule (ovo se dokazuje), tako da je u polju realnih brojeva uvek 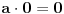 , tj proizvod dva broja je 0 ako i samo ako je jedan od tih brojeva 0.
matematika je vrlo razvijena nauka, i sve su šanse da je sve što ti ikad padne na pamet, pogotovo kao nematematičaru, neko nekad (po svoj prilici neki matematičar) već pomislio, promislio i razvio teoriju o tome. [ holononi @ 30.04.2009. 09:18 ] @
Citat: ima veze sa deliteljima nule
O kom polju je reč ? [ japan @ 30.04.2009. 09:26 ] @
ako se dobro sećam, nijedno polje nema pravih delitelja nule, jer po definiciji polja nula nema inverz, pa se onda lako dokazuje da polje nema pravih delitelja nule.
[ galet@world @ 30.04.2009. 10:05 ] @
@Fitopatolog
- Aksiom govori o poređenju jednakih (iste vrste) veličina
- Tačka je toliko mala da ne postoji, a s druge strane postoji kao oznaka nekog mesta,
dakle i postoji i ne postoji - jedinstvo suprotnosti po Imanuelu Kantu.
- da se i ja našalim: šestar ti ne valja jer ima vrh, a trebalo bi da ima tačku.
@Nedeljko
Neka osoba A stisne praznu šaku pa njen sadržaj izruči na dlan osobe B i neka to učini pet puta kao pozajmicu.
Ako je osoba B poštena kad bude vraćala dug izručiće sadržaj svoje prazne šake na dlan osobe A, ali ne jedanput
nego pet puta, uostalom, osoba A ima pravo na to.
@djoka_l
Za dve jedinice smo izmislili poseban znak koji izgleda ovako: 2
a za dve nule to nismo učinili - eto tu je diskriminacija
@holononi
Ipak smatram (a verujem i ti) da od istraživanja ne treba odustajati
@japan
Ovo o deliteljima nule nisam razumeo
[ holononi @ 30.04.2009. 10:09 ] @
Citat: ako se dobro sećam, nijedno polje nema pravih delitelja nule, jer po definiciji polja nula nema inverz, pa se onda lako dokazuje da polje nema pravih delitelja nule.
U tom slučaju, ovde smo razmatrali "dužinu kružnice" kao meru u skupu realnih brojeva. Ako to treba razmotriti u kontekstu neke strukture koja ima delitelje nule, tada definišite takvu strukturu i odgovarajuću meru.
Jer kao "meru dužine kružnice" mogu definisati sledeće:
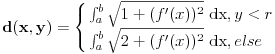
pa je kružnica "duža" "spolja" nego "iznutra". Ali ovakva definicija, ma kako bila izračunata "tačno" nije u skladu sa definicijama opšte prihvaćenim u ovakvim slučajevima. Zato može da bude opravdana samo u posebnim slučajevima koje treba jasno opisati. Ali tada dolazimo do toga da se sve može dokazati svim i svačim ako djipamo iz jednog konteksta u drugi bez prethodnog odredjivanja pravila. Kako se pravila odredjuju pre utakmice, tada nije pobedila ekipa koja je primila više golova iako to odgovara publici.
[ Fitopatolog @ 30.04.2009. 10:14 ] @
Citat: galet@world: Za dve jedinice smo izmislili poseban znak koji izgleda ovako: 2
a za dve nule to nismo učinili - eto tu je diskriminacija
Dve dvojke su četiri jedinice, ako se ne varam. Koliko je to nula? [ holononi @ 30.04.2009. 10:17 ] @
Citat: jedinstvo suprotnosti po Imanuelu Kantu
Ova tema nema veze sa Kantom.
Citat: Za dve jedinice smo izmislili poseban znak koji izgleda ovako: 2
Nije tačno, već 2 = 1 + 1, što ne utiče na ravnopravnost nule jer i dalje važi 0 + 0 + ... + 0 = 0, pa je nula donekle i privilegovana poput jedinice.
[ japan @ 30.04.2009. 10:34 ] @
Citat: holononi: U tom slučaju, ovde smo razmatrali "dužinu kružnice" kao meru u skupu realnih brojeva. Ako to treba razmotriti u kontekstu neke strukture koja ima delitelje nule, tada definišite takvu strukturu i odgovarajuću meru.
ako se vratiš na ono što sam napisao, videćeš da sam upravo to i rekao - da je u polju realnih brojeva 2*0 uvek jednako nula.
čisto sumnjam da je pokretač teme imao na umu strukturu koja ima delitelje nule, i meru u njoj, ali meni deluje da "ima neki osećaj" :) da takve strukture postoje, jedino što propušta je da u takvoj strukturi važe "druga pravila" i da se ta pravila ne mogu primeniti na realne brojeve. [ Nedeljko @ 30.04.2009. 10:40 ] @
@ galet@world
Pre nego što tvrdiš da je 0+0=0 glupost, imaj na umu da taj iskaz ide u paketu sa svojim kontekstom, a koji je određen definicijama koje mu prethode. Ovde svi govore o realnim brojevima, to jest o kompletnom uređenom polju, a to je struktura koja je zadata aksiomama. Svidele se tebi te aksiome ili ne, one imaju model i u tom modelu je 0+0=0, kao i svakom drugom modelu tih aksioma (čak su svi modeli tih aksioma međusobno izomorfni). Glupost nije tvrditi da je 0+0=0 u realnim brojevima, već tvrditi suprotno i to je vrlo lako dokazivo. Jednostavno 0+x=x je jedna od aksioma kompletno uređenih polja. Ako ne prihvataš te aksiome, onda radiš u nekoj drugoj strukturi, pa se i ne izjašnjavaš o ovoj jer je kontekst drugi. No, kompletno uređeno polje je vrlo strogo definisano za razliku od strukture koju ti zamišljaš i koju nigde nisi strogo uveo (aksiomama ili modelima, kako ti se više svidi).
[ Nedeljko @ 30.04.2009. 10:43 ] @
Citat: galet@world: @ Fitopatolog
dakle i postoji i ne postoji - jedinstvo suprotnosti po Imanuelu Kantu.
Zaboravio si na bratstvo. Tek zajedno sa bratstvom, jedinstvo može ovo da objasni. [ rajco @ 30.04.2009. 11:33 ] @
Moze li neko da me prosvetli pa da mi kaze o cemu prica ovaj covek?!(galet)
[ Farenhajt @ 30.04.2009. 12:14 ] @
Citat: rajco: Moze li neko da me prosvetli pa da mi kaze o cemu prica ovaj covek?!(galet)
Pokušava da uvede neku "zdravorazumsku" aksiomatiku realnih brojeva - kao, "bez nule" - ali siromah ne vidi da će onda da mu pukne i aksiomatika prirodnih/celih brojeva (kao pripadajućeg podskupa), te onda više nećemo moći da brojimo ovce i dobijemo tačan kusur u prodavnici.
Zaista će biti komedije... Žene će obožavati novu aksiomatiku, jer će, kad prevale određeni broj godina, moći sebe legitimno da podmlade za trideset osam puta nula godina i vratiće se u mladost... [ japan @ 30.04.2009. 12:43 ] @
Uh, nećeš se ti tako sprdati kad padne neka nova teorija Lobačevskog...
[ galet@world @ 30.04.2009. 13:27 ] @
Odgovoriću na sve primedbe (jer ih je mnogo) samo ovako:
Vi tvrdite da je 0 + 0 + 0 = 0
Ja tvrdim da je 0 + 0 + 0 = 3•0
Ja nisam ama baš ništa promenio, a vi jeste tvrdeći da su tri nule jednake jednoj.
[ Fitopatolog @ 30.04.2009. 13:35 ] @
Dane, zaboravio ("Zaboravio"?) si odgovor na glavno pitanje:
Citat: Fitopatolog: Dve dvojke su četiri jedinice, ako se ne varam. Koliko je to nula? [ Farenhajt @ 30.04.2009. 13:47 ] @
Citat: japan: Uh, nećeš se ti tako sprdati kad padne neka nova teorija Lobačevskog...
Sve se bojim  Lobačevski je uzduž i popreko znao Euklidovu aksiomatiku, pa joj je našao "rupu", dok ovaj nije čak ni matematičar, a kamoli da drži aksiomatiku realnih brojeva u malom prstu.
Ali već vidim korolare nove teorije realnih brojeva.
Teorema: Broj 1 je iracionalan.
Dokaz. Broj 1 možemo zapisati kao 1,000000... s beskonačnim brojem nula. Deljenjem razlomljenog dela mantise na [0][00][000][0000][00000] itd. (dakle, u svakom segmentu po jedna nula više nego u prethodnom), zaključujemo da razlomljeni deo mantise nije periodičan, te je broj 1 iracionalan. QED [ holononi @ 30.04.2009. 14:07 ] @
T: 0.317317317... je racionalan.
D: ?
[ Farenhajt @ 30.04.2009. 14:14 ] @
Citat: holononi: T: 0.317317317... je racionalan.
D: ?
Nisi se još temeljno saživeo s novom aksiomatikom. Racionalni brojevi ne postoje - svi su brojevi iracionalni. [ djoka_l @ 30.04.2009. 14:27 ] @
Ih, šta je Lobačevski!
Galet je već na elitesecurity oborio elektromagnetiku i STR, uzdrmao gravitaciju i OTR, raskomadao termodinamiku, a sada je došla na red matematika, počevši od Euklida, preko Njutna pa do danas.
Mislim da smo svedoci rađanja UTS (Univerzalne Teorije Svega)
Pamtiće se ovaj forum po novoj grani matematika koju bi smo mogli da zovemo Matematička intuicija.
[ NicholasMetropolis @ 30.04.2009. 14:48 ] @
Ja mislim da je konačno vreme za formiranje podforuma "Pseudonauka" gde će se forumski Don Kihoti boriti protiv vetrenjača dekadentne nauke.
[ Nedeljko @ 30.04.2009. 15:02 ] @
Citat: galet@world: Odgovoriću na sve primedbe (jer ih je mnogo) samo ovako:
Vi tvrdite da je 0 + 0 + 0 = 0
Ja tvrdim da je 0 + 0 + 0 = 3•0
Ja nisam ama baš ništa promenio, a vi jeste tvrdeći da su tri nule jednake jednoj.
Izvini, a ko ovde osporava da je 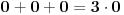 ? Kapiš? To uopšte nije sporno. Ti osporavaš da je 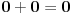 . Niko ne osporava da je 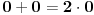 . [ holononi @ 30.04.2009. 15:19 ] @
Malo sam odremao dok ste to rešavali. Zadatak nisam ni namenio matematičarima.
Neki moji drugari (još iz detinjstva) hteli su da provere koliko matematičari znaju matematiku pa da mi daju neki zadatak. "M nemojte ljudi, puna mi je glava zadataka." Problem je bio koliko merenja, na običnim terazijama bez tegova, treba da se izmedju 13 kuglica pronadje jedina lažna. Oni su to rešili i pokazuju mi prste kojima su brojali kao dokaz. "Ma ne umem ja da brojim na prste, dajte to nekoj deci.". No bili su izuzetno uporni. Na kraju sam morao da rešim zadatak. Kako je medju njima bilo i diplomiranih inženjera elektrotehnike, pazio sam šta pričam, jer oni znaju matematiki u male prste. Pošto ne umem da računam na prste, morao sam da problem rešim za bilo koje N. Koristio sam se brojem reči dužine k nad p-azbukom. "Šta, gde, kako ?!@ Šta pričaš, ne lupetaj !". Bio sam zbunjen jer znam da na elektrothničkom rade takve stvari pa sam hteo da im uprostim dokaz. Da sam nekog mrzio koristio bih projektivnu geometriju ili nešto slično. Priča se završila tako što, evo, već nekih pet godina ti moji drugari ne govore sa mnom, samo mi se jave i dovidjenja.
[ galet@world @ 30.04.2009. 15:56 ] @
Nedeljko ja sam siguran da nisam promenio ništa, a vi ne znate da li ste nešto promenili
tvrdeći da su tri nule isto što i jedna.
holononi,citat:
"...vaše prebrojavanje istih ovaca neće povećati količinu mleka..."
Odustajem od prebrojavanja ovaca.
Nedeljko nastaviću kad prestanu blejanja koja se ne odnose na temu već na moj račun.
[ Farenhajt @ 30.04.2009. 16:05 ] @
Imamo mi još zanimljivih pitanja u Novoj teoriji realnih brojeva.
Odgovori nam, za početak, koliko je 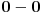 .
Odmah potom pređi na iznos 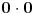 . [ Nedeljko @ 30.04.2009. 16:19 ] @
Citat: galet@world: Nedeljko ja sam siguran da nisam promenio ništa, a vi ne znate da li ste nešto promenili tvrdeći da su tri nule isto što i jedna.
Odakle ti ideja da govoriš u naše ime da li smo sigurni ili nismo? Ako ti nisi siguran, to je tvoj problem.
Citat: galet@world: Nedeljko nastaviću kad prestanu blejanja koja se ne odnose na temu već na moj račun.
Jeli, a to što se praviš gluv, ne slušaš šta drugi pričaju i samo teraš svoju priču, to nije blejanje.
Znaš kako, daj oglas da držiš časove svoje teorije realnih brojeva, pa ako ti se neko javi, slobodno raspredajte do mile volje. Ovakav "razgovor" nma nikakvog smisla. [ holononi @ 30.04.2009. 17:21 ] @
Citat: "...vaše prebrojavanje istih ovaca neće povećati količinu mleka..."
Odustajem od prebrojavanja ovaca.
Parabola u vezi ovaca ima svoj smisao u istorijskom kontekstu zasnivanja prirodnih brojeva i ništa drugo. Ukoliko neko u tome vidi nešto loše ja se izvinjavam na nedovoljno preciziranom stavu, te zato ova dopuna.
[ mokelet @ 30.04.2009. 19:08 ] @
Citat: galet@world:
Citat: mokelet: Da bi ti neko odgovorio na ovo "pitanje", moraš prvo da definišeš sledeće pojmove: broj, jednakost, veličina, veće, "toliko puta".
Slažem se, ali verujem da znaš šta sam hteo da kažem, a pomoć u tom pogledu mi je neophoda i svakako bi dobrodošla.
Ne, ne znam šta si hteo da kažeš. Intuitivno se frljaš sa terminima koje čak i različito koristiš u zavisnosti od potrebe. Onog trenutka kada budeš definisao svaki termin koji koristiš (i zasnovao sopstvenu aksiomatiku), tada ćemo moći da potvrdimo/opovrgnemo tvoju teoriju. Do tada, nema smisla diskutovati.
Mislim da je tema zrela za lock. [ galet@world @ 30.04.2009. 23:00 ] @
Mislio sam da ste spremni na saradnju u mom pokušaju istraživanja, ali očigledno sam se prevario.
Stoga ću ovim prilogom završiti moje učešće na ovoj temi.
[ holononi @ 30.04.2009. 23:41 ] @
Pobrkao si pojmove beskonačno velikih, beskonačno malih veličina, nule i beskonačno. Beskonačno nije broj u skupu realnih brojeva pa nisi ni mogao da podeliš te duži na beskonačan broj intervala. Nula je definisana aksiomima realnih brojeva i tu nema diskusije. Ti si se samo primakao dužini intervala nula i ostalo ti je da svaki od tih beskonačno malih intervala podeliš još bar beskonačno puta, bez ikakvih izgleda da dodješ do te drage nule. Mnogo jednostavnije ćeš pronaći nulu primenom aksioma x+(-x)=0 ili x*0=0. I to ti je jedina nula sigurica.
Mnogo bolje bi bilo da si obim one kružnice pokušao da odrediš upisanim i opisanim poligonima. Tada bi moglo da se govori o različitim dužinama spolja i iznutra, sve dok ne predješ na limes.
Nemoj da ovo shvatiš lično. Napadam STAV a ne ličnost.
[ mokelet @ 30.04.2009. 23:56 ] @
Čoveče, koji miks!
Stavio bih nekoliko primedbi na tvoju konstrukciju. Ti, naime, tvrdiš:
Citat: Duž AB nalazi se na dvostruko većem odstojanju 2l od tačke M
Postavlja se pitanje: kako možeš biti siguran da je to zaista dvostruko veće rastojanje, tj. na osnovu čega "fiksiraš" pojam dvostrukosti? I uopšte, koji pojam "rastojanja" (metrike) koristiš?
Zatim, u skladu sa tim, kako ćeš zaista biti siguran da si podelio duži ab i AB na jednake intervale, jer ako si u početnom postu tvrdio da je "unutrašnja" kružnica manja od "spoljašnje", po toj logici su intervali na sredini (a koji su bliži tački M) različite dužine od intervala na krajevima (koji su dalji od tačke M)?
Da li misliš na otvorene ili zatvorene intervale? Ako su u pitanju otvoreni intervali, "čija" je tačka koja deli dva intervala, pripada li ona levom ili desnom intervalu? Ako pripada i jednom i drugom intervalu, onda to znači da duž nije ni podeljena, dakle pripada ili jednom ili drugom. A to dalje znači da je jedan od tih intervala (koji sadrži tu tačku) duži od drugog (koji je ne sadrži), pa su onda ti intervali različiti, tj. jedan je veći od drugog za upravo tu tačku.
Ima puno rupa u tvojoj teoriji, a najviše zbog toga što upadaš u zamku geometrijske interpretacije pojmova iz analize. [ Fitopatolog @ 01.05.2009. 09:33 ] @
Dakle Dane, tresla se gora ...
Kada imaš dve beskonačno male (ili velike) "veličine" ne možeš ih upoređivati na standardan način, kao jabuke (evo, nisam napisao ovce!) već ih staviš u odnos i vidiš da li je rezultat konstanta (tada su istog reda) ili je rezultat beskonačno ili nula (tada nisu istog reda). Očigledno da su tvoje veličine i i(veznik) I istog reda. Da si uzeo npr. funkciju y=x*x i da si sa i označio da x teži 0, I bi bilo i*i i tada ove dve veličine ne bi bile istog reda. Svakako da ni i ni I NISU jednaki nuli iz prostog razloga što je reč (prema tvojoj interpretaciji) o limesu.
[ Nedeljko @ 01.05.2009. 11:25 ] @
Džabe se trudite. Galet jednostavno nikada nije prihvatio dijalektički metod na kome počivaju i matematika i celokupna nauka.
Uvedeš mu krušku po definiciji tako što mu je pokažeš i kažeš "ovo ćemo zvati kruškom", a on se "ne složi sa tim", bez obzira što definicije nisu stavovi da bi se neko složio sa njima ili ne.
@galet
U kompletnom uređenom polju je nemoguće podeliti duž na beskonačno mnogo jednakih delova. U nearhimedovskim je moguće, ali dužina podeljaka nije nula, već beskonačno mala veličina (ako nisi delio beskonačnu duž). To je drugo.
Sam priznaješ da ne znaš matematički jezik, ali osporavaš stavove kojima ne znaš značenje (jer ne znaš jezik na kome su formulisani) i uporno odbijaš da naučiš jezik.
[ zzzz @ 01.05.2009. 11:29 ] @
Istorijski početak razvoja matematike po mnogim autorima veže se za Pitagoru.I to
onaj period kada je otkriven iracionalan broj.Duboko uvjerenje da se svakoj
tački na brojnoj pravoj može doseći konačnim polovljenjem pogodnog intervala
naglo je poljuljano.Otkrili su da se površina trougla nad hipotenuzom, ako su katete jedinice iznosi dva.Na zaprepaštenje svih ispalo je da dužinu hipotenuze ne mogu izraziti racionalnim brojem, dakle taj broj postoji ali se ne može do njega nikako stići polovljenjem.
Meni izgleda da Dane želi povesti filozofsku raspravu sličnu ondašnjoj i krenuti
putem neke drukčije aksiomatike.Ali pritom koristi neka matematička dostignuća
dobivena na bazi usvojenih aksioma, što nebi smio.
Ako želi razviti novu alternativnu matematiku mora precizno definirati aksiome
odakle će krenuti.Može biti da će nešto korisno iz toga proizaći.
[ rincha @ 01.05.2009. 12:03 ] @
Ovo me podseca na konobarsku matematiku u kafani, 3x7=28 i nemam 2 dinara da ti vratim znaci 30.
Sa uzivanjem sam ispratio izlaganja i mogu samo da Vam kazem BRAVO.
Pozzz
[ holononi @ 01.05.2009. 13:06 ] @
Citat: Duboko uvjerenje da se svakoj tački na brojnoj pravoj može doseći konačnim polovljenjem pogodnog intervala naglo je poljuljano.
Čak i da dosegnemo odredjenu tačku na brojnoj pravoj, postavlja se pitanje kako doći do sledeće? U skupu prirodnih brojeva uvek znamo šta je pre  a šta posle  . Jer pre  je  a posle  je  . Ali u skupu relanih brojeva ne možemo sa konkretnog broja preći na prvi sledeći, jer ako posmatramo konkretan broj, na primer  koji je sledeći realan broj posle broja  ?
Prema tome, ako operišemo u skupu realnih brojeva onda uvek prvo braća aksiomi pa njihove sestre posledice. Sve ostalo mora da se dodefiniše. Pa ako uvedemo simbol ∞ onda moramo bar još toliko pojmova da dodefinišemo, na primer 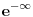 i slično.
Zato pri deljenju realnih brojeva moramo dobro paziti da se negde ne pojavi nula kao delioc jer deljenje nulom u skupu realnih brojeva nije definisano. Zato govorimo o odnosu dve veličine koje zavise od na primer  kad 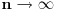 . Tada ćemo uvek dobiti da je odnos dužina odsečaka sa gornje i donje duži jednak 2, bez obzira što je reč o beskonačno malim veličinama.
[ mokelet @ 01.05.2009. 23:19 ] @
Citat: holononi:Ali u skupu relanih brojeva ne možemo sa konkretnog broja preći na prvi sledeći, jer ako posmatramo konkretan broj, na primer  koji je sledeći realan broj posle broja  ?
To je još jedan problem na koji galet@world i ne obraća pažnju. Naime, on koristi SAMO geometrijsku interpretaciju skupa realnih brojeva, tj. brojevnu pravu. Otud i njegovih nedoumica, kako bi tek bilo zamršeno apstrahovati skup R na neki drugi način.
Upravo kao što Holononi kaže, ne možeš da se koristiš aksiomama koje ne prihvataš. Pre svega, aksiomama incidencije, poretka, podudarnosti i paralelnosti, kako bi opovrgao aksiomu neprekidnosti. A da čak nismo ni zagrebali u analizu. Tragedija!
Btw, baš me zanima kakav stav ima galet@world o aksiomi paralelnosti! :-) [ Nedeljko @ 02.05.2009. 16:57 ] @
Galet, imam par pitanja za tebe:
1. Koliko rešenja ima jednačina x+2=2?
2. Koliko rešenja ima jednačina x+3=3?
[ galet@world @ 02.05.2009. 18:35 ] @
Jedno
[ Nedeljko @ 02.05.2009. 18:44 ] @
Odlično. Sada mi reci da li je rešenje prve jednačine istovetno rešenju druge jednačine.
[ galet@world @ 02.05.2009. 19:01 ] @
Rekao sam
[ galet@world @ 03.05.2009. 05:24 ] @
Nedeljko imam za tebe par pitanja:
1. Koliko zajedničkih tačaka ima kružnica prečnika od 2 metra sa svojom tangentom?
2. Koliko zajedničkih tačaka ima kružnica prečnika od 3 metra sa svojom tangentom?
[ mokelet @ 03.05.2009. 12:11 ] @
Citat: galet@world: Nedeljko imam za tebe par pitanja:
1. Koliko zajedničkih tačaka ima kružnica prečnika od 2 metra sa svojom tangentom?
2. Koliko zajedničkih tačaka ima kružnica prečnika od 3 metra sa svojom tangentom?
Definiši prvo šta je to "metar". [ holononi @ 03.05.2009. 12:46 ] @
Citat: Definiši prvo šta je to "metar".
Kako nema posebnih uslova podrazumeva se da je "metar" dat definicijom internacinalnog sistema mernih jedinica.
Nemojte da vrdate. Dobili ste pitanje, pa dajte odgovor.
[ Nedeljko @ 03.05.2009. 13:09 ] @
Što se tiče metra, strogo gledano on nije matematički pojam, jer se njegova definicija oslanja na svetlost i atom cezijuma. Međutim, to ne predstavlja problem u davanju odgovora na Galetovo pitanje
Citat: galet@world: Nedeljko imam za tebe par pitanja:
1. Koliko zajedničkih tačaka ima kružnica prečnika od 2 metra sa svojom tangentom?
2. Koliko zajedničkih tačaka ima kružnica prečnika od 3 metra sa svojom tangentom?
Dakle, kada se izabere jedinična duž, onda se ova pitanja mogu postaviti sa kružnicama prečnika 2 i 3. Stoga ovde nema svrhe cepidlačiti sa metrom, jer je pitanje sasvim jasno. Deder da dam i odgovor.
Svaka kružnica ima sa bilo kojom svojom tangentom tačno jednu zajedničku tačku.
Elem, da se vrnem na razlog zašto sam Galetu postavio ova pitanje.
Ako se ne varam, Galet se slaže s tim da postoji tačno jedan realan broj a takav da za bilo koji broj b važi a+b=b+a=b. E, pa vidiš, to je definicija nule. Nula je po definiciji realan broj u oznaci 0 takav da za ma koji realan broj x važi 0+x=x+0=x. Zamenjujući x sa 0, dobijamo da je 0+0=0. [ mokelet @ 03.05.2009. 13:16 ] @
Citat: holononi: Kako nema posebnih uslova podrazumeva se da je "metar" dat definicijom internacinalnog sistema mernih jedinica.
S obzirom da je u tom slučaju "metar" zadat sa tačnošću od 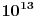 ( http://sr.wikipedia.org/sr-el/Metar), mislim da ne možemo da utvrdimo da li tangente zaista dodiruju kružnice prečnika 2 i 3 metra, naročito uzevši u obzir http://sr.wikipedia.org/sr-el/Relacije_neodre%C4%91enosti. [ holononi @ 03.05.2009. 13:29 ] @
Relcija neodredjenosti nije potrebna u ovom slučaju jer @galet@world verovtno napada prethodno date definicije. A osim toga relacija neodredjenoti se pre uklapa u "neodredjenost" realnog broja.
[ galet@world @ 03.05.2009. 15:28 ] @
Citat: Nedeljko:
Svaka kružnica ima sa bilo kojom svojom tangentom tačno jednu zajedničku tačku.
Prava je određena sa dve tačke ili sa jednom i smerom, a smer određuju susedne tačke kod
svake krive. Dosad je tangenta uvek prolazila kroz dve tačke. Bar smo tako učili, ali dobro,
pretpostavljam šta misliš - tangenta prolazi kroz jednu tačku a smer joj je normalan na radijus
zakrivljenosti u toj tački. Ovo je prihvatljivije od onog što sam učio o tangenti. OK.
Prava koja prolazi kroz dve susedne tačke odnosno deo prave koji prolazi kroz te tačke je
usvari granična tetiva.
Imaš li primedbu ili možda neko treće objašnjenje? [ japan @ 03.05.2009. 15:49 ] @
Citat: galet@world: Prava koja prolazi kroz dve susedne tačke odnosno deo prave koji prolazi kroz te tačke je
usvari granična tetiva.
šta su to susedne tačke? [ Nedeljko @ 03.05.2009. 16:35 ] @
Galet, ključna je ova stvar, koju ne komentarišeš:
Citat: Nedeljko: Ako se ne varam, Galet se slaže s tim da postoji tačno jedan realan broj a takav da za bilo koji broj b važi a+b=b+a=b. E, pa vidiš, to je definicija nule. Nula je po definiciji realan broj u oznaci 0 takav da za ma koji realan broj x važi 0+x=x+0=x. Zamenjujući x sa 0, dobijamo da je 0+0=0.
Molim te da obavezno odgovoriš na ovo.
A što se prave tiče, svaka prava prolazi kroz beskonačno mnogo tačaka, a jednoznačno je određena sa bilo koje dve ili sa jednom i sa pravcem. Opšta definicija tangente ide preko izvoda, ali ono što definitivno ne mogu da prihvatim su susedne tačke. [ galet@world @ 03.05.2009. 17:47 ] @
Citat: Nedeljko: Galet, ključna je ova stvar, koju ne komentarišeš
Ne brini, komentarisaću.
Pretpostavljam da nemaš primedbi na moje razmišljanje o tangenti jer tu nisi stavio primedbu.
Primedba se, prema tome, odnosi na tetivu.
Tetiva je duž koja spaja dve tačke na kružnici. Dužina tetive je rastojanje između tih tačaka.
Kolika je dužina granične tetive?
(Valjda znaš šta je granična ili najmanja tetiva ili ćeš opet da tražiš definiciju??)
[ mokelet @ 03.05.2009. 18:22 ] @
Citat: galet@world:
(Valjda znaš šta je granična ili najmanja tetiva ili ćeš opet da tražiš definiciju??)
Za sve vreme studiranja matematike nisam čuo za graničnu ili najmanju tetivu.
A koliko vidim, nije čuo ni Google: ""granicna tetiva"" i Google: ""najmanja tetiva""[ Nedeljko @ 03.05.2009. 18:32 ] @
Citat: galet@world: Pretpostavljam da nemaš primedbi na moje razmišljanje o tangenti jer tu nisi stavio primedbu. Primedba se, prema tome, odnosi na tetivu. Tetiva je duž koja spaja dve tačke na kružnici. Dužina tetive je rastojanje između tih tačaka.
Kolika je dužina granične tetive?(Valjda znaš šta je granična ili najmanja tetiva ili ćeš opet da tražiš definiciju??)
Kako nemam? Oslanjaš se na nepostojeći pojam "susednih tačaka". Gde god da su tačke A i B, postoji središte duži AB koje je između njih. Naravno da ne znam šta je granična tetiva, niti najmanja tetiva. [ holononi @ 03.05.2009. 18:35 ] @
U postu od 01.05.2009. u 13:06h navedeno je da se ne mogu izolovati dve susedne tačke u skupu realnih brojeva. Moguće je izolovati jednu tačku, ali kad se izoluje ta tačka tada nije moguće preći na sledeću susednu. Jer u skupu realnih brojeva izmedju svaka dva realna broja postoji realan broj. I taj proces se nikad ne završava.
Pojam granične tetive niuje definisan.
Kad su u pitanju kružnica i tangenta onda može da se postavi bolje pitanje. Naime, za očekivati je diskusije na temu šta je sa tangentom prave koja je u stvari kružnica beskonačnog prečnika. Koliko takva kružnica i njena tangenta imaju zajedničkih tačaka i to sve po definiciji izvoda.
[ japan @ 03.05.2009. 19:19 ] @
Citat: galet@world: Valjda znaš šta je granična ili najmanja tetiva ili ćeš opet da tražiš definiciju??
ja ne znam šta je to granična tetiva. pretpostavljam da je to duž koja spaja "susedne tačke" na kružnici? [ galet@world @ 03.05.2009. 20:11 ] @
Ako susedne tačke nisu definisane to ne znači i da ne mogu biti, a pogotuvu da ne postoje.
Postojanje nečega ne zavisi valjda od postojanja definicije. Činjenica je da tetive postoje
i da je najveća jednaka prečniku kružnice, činjenica je takođe da postoji tangenta koja nije
tetiva.
Maksimalna dužina tetive je prečnik, a koja je minimalna ponovo pitam.
Izjava "Naravno da ne znam šta je granična tetiva, niti najmanja tetiva" je poražavajuća.
To uopšte nije "naravno", osim ako ne uvedemo princip da za sve što ne znamo kažemo da je naravno
Kako se može u matematici ostaviti pojam tetive u tolikoj meri nedorečen?
Pokušajte bar preko limesa.
[ holononi @ 03.05.2009. 20:21 ] @
Citat: šta je to granična tetiva. pretpostavljam da je to duž koja spaja "susedne tačke" na kružnici?
Ako je to definicija granične tetive opet ostaje problem izolovanja susednih tačaka. Kad bi mogli da izolujemo dve susedne tačke u skupu realnih brojeva, tada bi mogli da sve realne brojeve poredjamo u niz. Posle svakog realnog broja dolazio bi sledeći realan broj. Dobili bi da je skup realnih brojeva poredjan u niz pa tim i prebrojiv. Medjutim, skup realnih brojeva nije prebrojiv. Za dokaz, pogledati tvrdjenje Kantora o neprebrojivosti intervala. Takodje pogledati aksiom neprekidnosti i njegove posledice.
[ galet@world @ 03.05.2009. 22:33 ] @
Pogledajmo malo ovaj rezon:
Ako imamo neki četvorougao A B C D pa mu smanjujemo recimo stranu C D
Četvorougao ostaje kao pojava sa svojim svojstvima sve dok postoje uglovi C i D
odnosno stranica C D. Onog trenutka ( ne bi trebalo uzimati vremenske termine ali...)
kad tačka C i D budu na istom mestu dobijamo trougao - dakle novu pojavu - taj
prelaz događa se odjednom skokovito a ne postepeno.
Isto tako ako neka prava preseca kružnicu u dve tačke A i B - deo te prave je tetiva.
Ako tu pravu rotiramo oko tačke B tako da se dužina tetive smanjuje t. j. da se tačka
A približava tački B tetiva će se kontinualno smanjivati. Dok god postoji tačka A na
nekom mestu na kom nije tačka B - tetiva postoji. U trenutku kada tačka A padne
na mesto tačke B tetiva više ne postoji - prava je prešla u novu pojavu postala je
tangeta i to skokovito - odjednom. Ako je tačka A krećući se kontinualno došla na
isto mesto gde se nalazi tačka B onda je neposredno pre toga morala biti i susedna
tačka tački A. U tom trenutku tetiva još uvek postoji jer postoje dve tačke, a
rastojanje između njih je nula i ta nula ima dimenziju dužine upravo zato što tu još nije
jedna tačka nego dve.
[ japan @ 03.05.2009. 22:50 ] @
tačke realnoj pravoj, kružnici, ili čemu god, nisu klikeri pa da mogu biti susedni u jednom trenutku, ili da se poklapaju u nekom drugom. lepo si dobio objašnjenje da između dve različite realne tačke uvek postoji beskonačno mnogo tačaka.
a reci mi galet, znaš li ti koja je razlika između realnih i racionalnih brojeva?
[ holononi @ 03.05.2009. 23:21 ] @
Citat: postoje dve tačke, a rastojanje između njih je nula
Rastojanje izmedju dve tačke, recimo x i y, d(x,y) = 0 ako i samo ako x = y.
[ Nedeljko @ 04.05.2009. 07:42 ] @
Citat: galet@world: Ako je tačka A krećući se kontinualno došla na isto mesto gde se nalazi tačka B onda je neposredno pre toga morala biti i susedna tačka tački A.
Pojam "neposredno pre" (tj. susednih trenutaka) je sporan kao i pojam susednih tačaka. Tu nema suštinske razlike.
Citat: galet@world: Ako susedne tačke nisu definisane to ne znači i da ne mogu biti, a pogotuvu da ne postoje. Postojanje nečega ne zavisi valjda od postojanja definicije.
Iz pretpostavke da postoje se dobija kontradikcija (jer svaka duž ima središte), što svakako znači da ne postoje.
Citat: galet@world: Kako se može u matematici ostaviti pojam tetive u tolikoj meri nedorečen?
Tetiva je sasvim dorečen pojam - duž koja spaja dve tačke kruga. Ako sadrži te dve tačke, onda je zatvorena, ako ih ne sadrži, onda je otvorena.
U limesu tetiva prelazi u tačku. [ galet@world @ 04.05.2009. 09:19 ] @
Citat: holononi: Rastojanje izmedju dve tačke, recimo x i y, d(x,y) = 0 ako i samo ako x = y.
To je ipak samo kazivanje, ali ne i dokazivanje. Osim toga u ovom slučaju nema rastojanja jer se ne radi o dve tačke, odnosno
o dva mesta nego o jednom istom mestu pa govoriti o rastojanju nekog mesta od samog sebe nema smisla jer ono ne postoji.
Ako ima smisla govoriti o tome onda ta nula označava nepostojanje i to je nula koja se dobija oduzimanjem dveju
jednakih veličina na pr.: a - a = 0. Takva nula nema dimenziju ma šta označavali simboli a t.j. imali oni dimenziju
ili ne.
Nedeljko, na primer, kaže da je 
Ova jednakost nije istinita. Ako, na primer, cifre 1 i 3 označavaju neke dužine onda desna strana ove jednačine predstavlja
nulu bez dimenzije - ta strana označava nepostojanje dužine odnosno nepostojanje uopšte. Leva strana označava nulu koja
ima dimenziju dužine jer je dužina 1 podeljena na beskonačno mnogo delova i ona se opet može dobiti obrnutim postupkom.
Ranije sam naveo primer da samo tačke na preseku dveju ravni pripadaju obema ravnima. Ako isključimo te tačke onda dve
ravni više ne postoje nego četiri poluravni sa međusobnim rastojanjem nula.
Dakle postoje dve različite nule
1. Nula koja označava nepostojanje i koja nema dimenziju - to je nula koja je definisana i koju sad komentarišem
2. Nula koja ima dimenziju i koja je uporediva sa drugim takvim nulama o čemu navodim primer u prilogu
Za nulu pod 1. važi da je n•0 = 0 jer od nepostojanja se ne može dobiti ništa čak i ako je  jer
ta nula nema dimenziju ni dužine ni površine niti bilo čega pa ni rezultat ne može imati dimenziju
Za nulu pod 2. to ne važi jer je proizvod n•0 veći od takve nule n puta i tu je pogrešno pisati n•0 = 0, a ukoliko
je  onda je rezultat konačna veličina sa dimenzijom koju ima ta nula. Ovde bi, naravno, trebalo
dodefinisati još mnogo toga, ali ovo za sad predstavlja samo ideju neukog čoveka koju neki vrsan i učen matematičar
može razraditi, proveriti i definisati.
Izvini Nedeljko tvoju poruku sam video tek pošto sam poslao moju pa ću zasad da ti odgovorim samo na ovo
Citat: U limesu tetiva prelazi u tačku.
Limes neke pojave ne može biti neka druga pojava
[Ovu poruku je menjao galet@world dana 04.05.2009. u 10:34 GMT+1][ Nedeljko @ 04.05.2009. 10:52 ] @
Citat: galet@world: To je ipak samo kazivanje, ali ne i dokazivanje. Osim toga u ovom slučaju nema rastojanja jer se ne radi o dve tačke, odnosno o dva mesta nego o jednom istom mestu pa govoriti o rastojanju nekog mesta od samog sebe nema smisla jer ono ne postoji.
To je sastavni deo definicije metrike, a definicije se ne dokazuju. To je kao kada bi dokazivao oznake.
Ako se govori o konkretnoj metrici, recimo rastojanju tačaka u ravni, onda se za uvedenu funkciju mora prvo dokazati da zadovoljava aksiome metrike, da bi se onda ona koristila kao funkcija rastojanja.
Za tačke  i 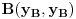 euklidsko rastojanje između njih se definiše kao 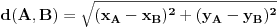 . Do sada je koren iz svakog pozitivnog realnog broja bio pozitivan realan broj, pa ako je koren nekog realno broja 0, onda je taj realan broj 0. Zbir kvadrata dva realna broja od kojih je bar jedan različit od 0 je pozitivan, pa ako je zbir dva kvadrata realnih brojeva 0, onda su ti realni brojevi jednaki 0. Ako je razlika dva realna broja 0, onda su ti realni brojevi jednaki. Tačke sa istim koordinatama su jedna ista tačka.
Citat: galet@world: Limes neke pojave ne može biti neka druga pojava
Za ovo ćeš morati da definišeš pojam pojave i pojam limesa pojave. [ holononi @ 04.05.2009. 10:58 ] @
Citat: To je ipak samo kazivanje, ali ne i dokazivanje.
U tom slučju evo i dokaza:
Na realnoj pravoj rastojanje kao mera se daje u obliku d(x,y) = |x - y|.
Stav: d(x,y) = 0 <=> x = y
Dokaz:
(=>) d(x,y) = 0 => x = y
Pretpostaviti suprotno, x <> y. Tada postoji c iz (x,y) pa je
d(x,y) = d(x,c) + d(c,y) = 0 odnosno
d(x,c) = -d(c,y) = -|c - y| < 0
što je kontradikcija jer je d(x,c) = |x - c| > 0
(<=) x = y => d(x,y) = 0
Neka je x = y, tada
d(x,y) = d(x,x) = d(y,y) = |x - x| = |y - y| = 0
* kraj dokaza *
Inače, za one koje ova problematika interesuje više u PSEUDOmetrici je dozvojen slabiji uslov x=y => d(x,y)=0.
Citat: Dakle postoje dve različite nule
Nikako, jer neutralni element sabiranja je jedinstven. Sledi iz aksioma realnih brojeva.
Citat: Limes neke pojave ne može biti neka druga pojava
Može, pogledaj definciju izvoda funkcije i geometrijsku interpretciju.
Što se tiče crteža porediš dve beskonačno male veličine, što je u redu. Ali ti zaključak nije tačan jer si zaboravio iz srednje škole da je 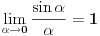
[ Nedeljko @ 04.05.2009. 11:04 ] @
Hajde da proverimo. Nula je po definiciji broj koji sabran sa bilo kojim brojem x daje isti taj broj x.
Pretpostavimo da imamo dve nule, 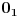 i 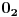 . Obzirom da je 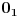 nula, važi 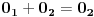 . Obzirom da je 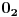 nula, važi 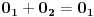 . Dakle, 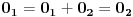 .
[ djoka_l @ 04.05.2009. 11:05 ] @
Opet jedno intuitivno tvrđenje:
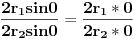
pa kad skratimo sa 0 dobijamo nebulozu. [ Nedeljko @ 04.05.2009. 11:06 ] @
Citat: galet@world: Dakle postoje dve različite nule
1. Nula koja označava nepostojanje i koja nema dimenziju - to je nula koja je definisana i koju sad komentarišem
2. Nula koja ima dimenziju i koja je uporediva sa drugim takvim nulama o čemu navodim primer u prilogu
Jok vala! Standarnim terminima se ne mogu pridru\žvati druga značenja. Za nove pojmove moraš uvesti nova imena i oznake. [ galet@world @ 04.05.2009. 19:22 ] @
Citat: holononi: U tom slučju evo i dokaza:
Ovo bi bio dokaz za jednakost dvaju intervala (x i y). Rastojanje između tačaka je jedan interval.
Rastojanje postoji dok postoje dve tačke na različitim mestima.
Rastojanje između dve tačke na istom mestu ne postoji jer je sasvim svejedno da li na jednom mestu
postoji jedna ili dve tačke. Nepostojanje rastojanja označava se sa nulom koja nema dimenziju.
Treba razlikovati nepostojanje rastojanja od rastojanja koje je jednako nuli koja ima dimenziju dužine.
Nepostojanje rastojanja znači da nema intervala, a nula sa dimenzijom dužine ne ukida ni tačke ni
rastojanje.
Koliko je rastojanje između poluravni u primeru sa dve ravni koje se seku ako smo isključili zajedničke tačke?
Citat: Nikako, jer neutralni element sabiranja je jedinstven. Sledi iz aksioma realnih brojeva.
Samo nepostojanje je neutralni element sabiranja i označava se sa nulom bez dimenzije.
Citat: Može, pogledaj definciju izvoda funkcije i geometrijsku interpretciju.
Na primer?
Citat: što je u redu. Ali ti zaključak nije tačan jer si zaboravio iz srednje škole da je 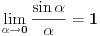
Ovo važi u svim školama bilo kog nivoa (čemu podrugljivost?), ali ja to nisam zaboravio. Pre će biti da si ti
zaboravio da je odnos tetiva kružnica različitih prečnika za isti ugao jednak odnosu radijusa. Taj odnos se
ne menja bez obzira na veličinu ugla.
Citat: Nedeljko: Hajde da proverimo. Nula je po definiciji broj koji sabran sa bilo kojim brojem x daje isti taj broj x.
Zašto insistiraš na ovom? Pa s tim se ja slažem i to važi za nulu koja nema dimenziju. Tvoja računica sa
nulama koje označavaju granične dužine tetiva nije u redu jer to nisu nule bez dimenzije.
Citat: djoka_l: pa kad skratimo sa 0 dobijamo nebulozu.
Nismo skraćivali s nulom nego sa sinusom i nismo dobili nebulozu
Nedeljko opet prevideh:
"Za nove pojmove moraš uvesti nova imena i oznake."
Slažem se. Nula bez dimenzije t. j. nula koju ti priznaješ mogla bi se označavati sa precrtanom nulom jer označava
nepostojanje (to se ponegde i radi da bi se nula razlikovala od od slova O), a nula sa dimenzijom bi se označavala
kao i do sada i s njom bi trebalo računati kao sa opštim brojem, međutim, ima tu još mnogo toga što bi trebalo
razmotriti i definisati.
[Ovu poruku je menjao galet@world dana 04.05.2009. u 20:36 GMT+1][ holononi @ 04.05.2009. 22:08 ] @
Citat: (čemu podrugljivost?)
Izvinjvam se ali nije mi namera da budem podrugljiv. Ako nisi zaboravio onda ne znaš da je deljenje nulom nedozvoljeno. Ti si u tvom primeru skratio nulom,
2r 1sin0 0 / (2r 2sin0 0) = r 1 / r 2
što nikako ne može jer je sin0 0 = 0. Moglo bi nešto poput lim(sinx/siny) kada x i y teže nuli.
Prvi deo posta u kome opovrgavaš dokaz koji sam izveo neću da komentarišem jer takvo opovrgavanje nema veze sa matematikom.
Citat: Nismo skraćivali s nulom nego sa sinusom i nismo dobili nebulozu
Ako si skraćivao beskonačno male veličine, trebao si preći na limes, kako si i sam primetio. Tada bi videli da li bi dobili 1/1 ili nešto drugo.
Citat: Nula bez dimenzije t. j. nula koju ti priznaješ mogla bi se označavati sa precrtanom nulom jer označava nepostojanje (to se ponegde i radi da bi se nula razlikovala od od slova O), a nula sa dimenzijom bi se označavala kao i do sada i s njom bi trebalo računati kao sa opštim brojem
Prazan skup {} u matematici označava nepostojanje i nije potrebno uvoditi novi simbol za to. Nula je takodje dobila svoje mesto kao BROJ u skupu realnih brojeva i teško ćemo ubediti svet da uvede novi simbol za nešto što je već dato.
Svi koji učestvuju u diskusiji na ovom forumu treba da prihvate neku dozu odgovornosti. Imajte na umu da bi ove postove mogao da čita neko ko tek uči matematiku. Posebno da će ovi postovi biti dostupni i kroz 10-20 godina a kako se informatika razvija verovatno i dugo nakon što mi prestanemo da budemo aktivni članovi ovih diskusija. Oni koji se tek uče treba da dobiju informacije koje će ih pravilno usmeriti u svojim razmišljanjima i sticanju znanja o osnovnim matematičkim pojmovima. Budući da neki uporno odbijaju da prihvate elementarne stavove matematike postavlja se pitanje održavanja ovog foruma. No kako se ovaj forum neće ukinui čak i ako bi neko od nas prekinuo da odgovara na postove, dovedeni smo u poziciju da moramo da pobijamo stavove koji i nemaju mnogo utemeljenja u matematici. Zao bih molio sve da uzmu u obzir da bi neko ko se tek uči mogao usvojiti dosta spornih stavova, što se kasnije jako teško ispravlja a može da nanese i trajnu štetu učeniku.
[ mokelet @ 04.05.2009. 22:14 ] @
Citat: galet@world:Ovo bi bio dokaz za jednakost dvaju intervala (x i y). Rastojanje između tačaka je jedan interval.
Nisi pažljivo pratio, u pitanju je dokaz za razdaljinu između tačaka x i y. Nikakva dva intervala se ne spominju. Dokaz je toliko jednostavan i lep, da je prosto tužno što ga nisi pogledao i razumeo.
Citat: galet@world:Rastojanje između dve tačke na istom mestu ne postoji jer je sasvim svejedno da li na jednom mestu
postoji jedna ili dve tačke.
Hoćeš da kažeš ovo:
"Sasvim je svejedno da li na jednom mestu postoji jedna ili dve tačke"  "Rastojanje između dve tačke na istom mestu ne postoji"?
Dokaži!
Citat: galet@world:Nepostojanje rastojanja označava se sa nulom koja nema dimenziju. Nepostojanje rastojanja znači da nema intervala, a nula sa dimenzijom dužine ne ukida ni tačke ni
rastojanje.
Nepostojanje/postojanje, netačno/tačno i sl. predstavljaju logičku kategoriju i mogu se označiti sa nulom (odnosno jedinicom), kao i drugim ciframa/slovima/rečima/znakovima. Naravno da ta nula nema dimenziju, jer to nije ista nula (odnosno oznaka) o kojoj pričamo kada govorimo o rastojanju (koje je definisano kao metrika). Ali te dve nule se ne mogu koristiti u istom kontekstu, to bi bilo kao kada bismo tebe zvali "Ubrzanje sile zemljine teže alet", jer eto slovo "g" označava pomenuto ubrzanje, dok smo za ostala slova odlučili da ih koristimo kao znakove koji odgovaraju glasovima u srpskom jeziku.
Jednostavno, radi se o babama i žabama.
Citat: galet@world:Koliko je rastojanje između poluravni u primeru sa dve ravni koje se seku ako smo isključili zajedničke tačke?
Rastojanje je 0 (nula). Zaboravio si da tačka nema dimenziju?
Citat: galet@world:Samo nepostojanje je neutralni element sabiranja i označava se sa nulom bez dimenzije.
Nula (0) je neutralni element sabiranja, nepostojanje je, kao što rekoh, logička kategorija. Ali u pravu si da nula u logici nema dimenziju (na način na koji ti koristiš pojam "dimenzija").
Šta ti u stvari tvrdiš na kraju? Možeš li to da sažmeš u par rečenica, napravi neku teoriju, neki skup aksioma i definicija kojoma tvrdiš to što tvrdiš. [ Farenhajt @ 04.05.2009. 22:48 ] @
Ja u ovom trenutku imam načelno pitanje.
Ovo je UBEDLJIVO najživlja diskusija na celom matematičkom forumu, na kojoj učestvuje više diskutanata koji dokazano dobro barataju matematikom, a ipak ih - s oproštenjem na izrazu - teranje ćorava posla neodoljivo privlači, te se iznova i iznova vraćaju s kilometarskim objašnjenjima elementarnih stvari jasnih kao dan.
U čemu je stvar? Zašto?
Neodoljiva privlačnost iluzije da će se Gaćeša "prosvetliti" samo ako mu se jedne te iste stvari ponove dovoljan (ali, reklo bi se, neprebrojiv) broj puta? Neće.
Ili zaista nemate šta pametnije da radite, niti kako kreativnije da doprinesete ovom forumu i(li) ispunite slobodno vreme? Pa, do đavola, okačite neki zanimljiv i dobar problem koji ste našli u literaturi, sreli u praksi ili pak sami smislili, ili uzmite pa rešite neki od objavljenih zadataka. To će mnogo više doprineti svačijem matematičkom čulu i znanju nego insistiranje na apsolutno somnambulnim diskusijama.
[ Nedeljko @ 05.05.2009. 11:04 ] @
Citat: galet@world: Zašto insistiraš na ovom? Pa s tim se ja slažem i to važi za nulu koja nema dimenziju.
Prihvataš zakon 0+x=x, a ne prihvataš zakon 0+0=0. Zanimnljivo!
Citat: galet@world: Nedeljko opet prevideh:
"Za nove pojmove moraš uvesti nova imena i oznake."
Slažem se. Nula bez dimenzije t. j. nula koju ti priznaješ mogla bi se označavati sa precrtanom nulom jer označava
nepostojanje (to se ponegde i radi da bi se nula razlikovala od od slova O), a nula sa dimenzijom bi se označavala
kao i do sada i s njom bi trebalo računati kao sa opštim brojem, međutim, ima tu još mnogo toga što bi trebalo
razmotriti i definisati.
Nula je po definiciji neutralni element za sabiranje i ne može značiti ništa drugo. Za sve ostalo moraš koristiti drugu terminologiju. Oznaka 0 označava samo nulu, to jest neutralni element za sabiranje i ne može označavati ništa drugo. Ponegde se precrtava, zbog razlikovanja od slova "O", to je tačno, ali nema veze sa ovom temom.
Ovo što radiš je teranje ljudi da kupus zovu "paradajz", paradajz da zovu "šargarepa", šargarepu da zovu "krompir" i tako dalje, samo da bi tebi udovoljili. To ne dolazi u obzir. [ galet@world @ 05.05.2009. 11:13 ] @
Citat: Farenhajt: Neodoljiva privlačnost iluzije da će se Gaćeša "prosvetliti" samo ako mu se jedne te iste stvari ponove dovoljan (ali, reklo bi se, neprebrojiv) broj puta? Neće.
Zamolio bih tebe i sve ostale učesnike u raspravi da me ne pominju ni po imenu ni drukčije. Ne smatram
da si primitivan pa zato verujem da ćeš uvažiti ovu moju molbu. Nomina sunt odiosa. Imaš temu
i raspravljaj o njoj ako hoćeš i ti i ostali. Tvoji saveti odraslim ljudima su neumesni jer niko ovde nije u
poziciji da bi mu neko savetovao šta da čini i kako da se ponaša.
Citat: holononi:Ako nisi zaboravio onda ne znaš da je deljenje nulom nedozvoljeno.
Ti si u tvom primeru skratio nulom,što nikako ne može jer je sin0 0 = 0. Moglo bi nešto poput
lim(sinx/siny) kada x i y teže nuli
Deljenje znači i poređenje. Ja sam u konkretnom slučaju poredio dve nule jer im znam poreklo i znam da
su jednake i znam je sinx/sinx = 1 za svako x, ali ne znam odakle ti y jer je ugao i kod velike i male
kružnice isti.
Citat: Ako si skraćivao beskonačno male veličine, trebao si preći na limes, kako si i sam primetio.
Tada bi videli da li bi dobili 1/1 ili nešto drugo.
Nema potrebe jer je u konkretnom slučaju odnos među tetivama kružnica konstantan i ne menja se ako
je ugao nasuprot tetiva isti ma koliki on bio.
Citat: Nula je takodje dobila svoje mesto kao BROJ u skupu realnih brojeva
S tim se slažem, ali samo za nulu koja označava nepostojanje.
Citat: Svi koji učestvuju u diskusiji na ovom forumu treba da prihvate neku dozu odgovornosti.
Naravno, ali ukidanje foruma ne bi pomoglo u proglašavanju odgovornog već bi to značilo bežanje od
odgovornosti.
Citat: mokelet: Dokaz je toliko jednostavan i lep, da je prosto tužno što ga nisi pogledao i razumeo.
Pogledaj malo bolje ovaj citat:
Citat: Na realnoj pravoj rastojanje kao mera se daje u obliku d(x,y) = |x - y|.
Tužnije je to što ti ne vidiš šta je x i šta je y. Ovi simboli označavaju položaj tačaka, a ne oznake, oznake
se valjda ne mogu oduzimati
Citat: Hoćeš da kažeš ovo:..(sledi citat)..Dokaži!
Ako staviš jednu tačku na drugu to ti je isto kao da nisi uradio ništa - opet možeš smatrati kao da je tu
samo jedna tačka. Pa pitanje koliko je rastojanje između t a č k e nema smisla.
Citat: to bi bilo kao kada bismo tebe zvali "Ubrzanje sile zemljine teže alet", jer eto slovo "g" označava pomenuto ubrzanje
Ili "Masa naše planete okelet, jer eto slovo "m" označava pomenutu masu". Još tužnije!
Citat: Rastojanje je 0 (nula). Zaboravio si da tačka nema dimenziju?
Rastojanje si pogodio, ali da sam zaboravio to nisi.
Citat: Šta ti u stvari tvrdiš na kraju? Možeš li to da sažmeš u par rečenica, napravi neku teoriju, neki skup aksioma i definicija kojoma tvrdiš to što tvrdiš.
Pa kad nećeš da pomogneš, a ja ne umem! Pokazao sam na primeru sa tetivama da su te nule međusobno različite i
još da se razlikuju i od "zvanične" nule. A imam još jedan zgodan primer ako te interesuje. [ galet@world @ 05.05.2009. 11:35 ] @
Citat: Nedeljko: Prihvataš zakon 0+x=x, a ne prihvataš zakon 0+0=0. Zanimnljivo!.
Prihvatam zakon 0+x=x i 0+0=0 ako su nule bez dimenzije, a ako nisu onda ne prihvatam ništa od toga
0+x>x ako je x neka duž, a podvučena nula neka granična tetiva
Citat: Ovo što radiš je teranje ljudi da kupus zovu "paradajz", paradajz da zovu "šargarepa", šargarepu da zovu "krompir" i tako dalje, samo da bi tebi udovoljili. To ne dolazi u obzir.
Ne teram nikoga ni na šta, ali ako sam u pravu moraće se u označavanju nešto prihvatljivo smisliti. [ galet@world @ 05.05.2009. 11:38 ] @
Još jednom molim fer raspravu
[ japan @ 05.05.2009. 13:18 ] @
rasprava bi mogla da bude fer kada bi ti baratao osnovnim pojmovima matematičke analize, kao što su limes, diferencijalni račun i sl. i kada bi znao da ne možeš tek tako da primenjuješ pravila diskretnih struktura na kontinualne.
ovako, rasprava nikako ne može da bude fer - uvek će biti borba između amaterske pero lake i profesionalne super teške, ti ćeš uvek otkrivati toplu vodu i rupu na saksiji, pokušavajući da opovrgneš opšteprihvaćene teorije uspostavljene pre 150 i 200 godina, a ostali, mahom matematičari, koji su sa tim teorijama upoznati i shvataju njihovu suštinu, će se sprdati sa tvojim izjavama i teorijama, ili će, u najboljem slučaju, pokušavati da ti ukažu na greške u rezonu, ali potpuno bezuspešno, jer pri tome moraju da se koriste _matematičkim_ pojmovima i zakonima, a ti iste ne prihvataš, nego pokušavaš da uspostaviš nekakvu intuicionističku matematiku, analognu pojavama koje možeš da _vidiš_ u prirodi oko sebe, i da uvedeš nove pojmove u skladu sa tim, pa onda tačke na realnoj pravoj gledaš kao klikere i uvodiš pojam "susednih tačaka", daješ dimenzije nuli i slične (nemoj shvatati lično) budalaštine.
ako te ova tematika stvarno zanima, moj iskreni savet ti je da se dooooooobro upoznaš sa materijom, pa tek onda da tražiš rupe u njoj. [ holononi @ 05.05.2009. 13:45 ] @
Odgovor na stavove kao što su o nuli "koja označava nepostojanje" bi predstavljao samo ponavljanje već rečenog. Iskazi poput "s tim se ne slažem" i slično bez matematički zasnovanih argumenata u matematičkom smislu nemaju nikakvu verednost. Diskusija gubi na smislu jer neki diskutanti ne uočavaju elemntarne stavove o beskonačno malim i beskonačno velikim veličinama. Da nevolja bude još veća, svaku digresiju na odgovarajuću referencu diskutanti smatraju uvredljivom pri tom odbijajući da prihvate bilo kakvu misao o potrebi proširivanja sopstvenog znanja. Lično sam pročitao na desetine hiljade knjiga, časopisa i publikacija. Medjutim, jednu od istina koju sam uočio u poslednjih mesec dana potiče od primedbe 12-godišnjeg deteta. Nije to zato što mi je dete "solilo pamet". Ono i ne zna o čemu je reč, samo što ja redovno "perem uši".
Bilo bi lepo reći da imam 1 dinar u džepu jer se ne slažem s tim da mi je džep prazan. Ali to neće promeniti stvarnost samo zato što sam to ja rekao.
[ galet@world @ 05.05.2009. 19:06 ] @
Ovakve priče su predugačke i van teme. Ako je neko doveden u logički škripac ne razumevajući
postojanost odnosa u konačnim i beskonačnim domenima onda naravno ne može ni da kaže
ništa drugo osim onog što je naučio i to bez razumevanja. Opsednutost raznim teorijama, problematičnim
aksiomima, teoremama i ko zna čime još je van svake sumnje kočnica i prepreka za nova otkrića.
Stoga mi ne pada napamet da ih proučavam pogotovu stoga što njihovi poznavaoci ne mogu
dati adekvatan odgovor na jednostavna pitanja ili se na ovaj ili onaj način sujetno suprotstavljaju
rešenjima za koja znaju da su tačna.
[ mokelet @ 05.05.2009. 21:32 ] @
Citat: galet@world:Ako je neko doveden u logički škripac ne razumevajući
postojanost odnosa u konačnim i beskonačnim domenima onda naravno ne može ni da kaže
ništa drugo osim onog što je naučio i to bez razumevanja.
Nemam reči, osim možda :-)
Citat: galet@world:Opsednutost raznim teorijama, problematičnim
aksiomima, teoremama i ko zna čime još je van svake sumnje kočnica i prepreka za nova otkrića.
Ako si raspoložen za nova otkrića, a vidim da poseduješ fantastičan entuzijazam za hvatanje u koštac sa fundamentima matematike, toplo ti preporučujem http://www.claymath.org/millennium/
Zaista bih voleo da čujem tvoje mišljenje o tome. [ holononi @ 05.05.2009. 22:23 ] @
Da li se neko seća "Makedonskog algoritma" za odredjivanje korena, kako su autori tvrdili "nerešivih jednačina" i to za samo nekoliko minuta olovkom. Članci o dvojici matematičara su izašli u časopisu "Računari u vašoj kući" pre 20 i kusur godina. Zanim me kako se završila ta priča.
[ galet@world @ 06.05.2009. 08:13 ] @
Citat: mokelet: Zaista bih voleo da čujem tvoje mišljenje o tome.
Mnogo je nerešenih problema u matematici. Rešiti bilo koji je velika stvar. Ja,na primer, pokušavam
da dokažem da se sa nulama koje imaju dimenziju može računati i da se one mogu upoređivati isto
kao i sa opštim brojevima, ali im se mora znati poreklo (kako su nastale odnosno od čega su one
rezultat).A evo i problema koji izgleda jednostavan, ali kad se malo udubiš onda nije:
Kako izračunati dužinu kružnice?
Ako kružnicu podeliš na delove odnosno lukove i te lukove poređaš na neku pravu liniju tako da
se tetive tih lukova poklapaju s tom linijom onda dobijaš aproksimaciju dužine kružnice sabirajući
dužine tetiva. Što više usitnjavaš lukove dobijaš sve bolju aproksimaciju. Kada dužine tetiva teže
nuli onda sume sve sitnijih tetiva teže nekoj graničnoj vrednosti. I onda mi kažemo da je dužina
kružnice jednaka dužini neke prave duži, međutim, ako kolonu poređanih lukova presečemo na bilo
kom mestu - na tom mestu postoji zakrivljenost koja je konstantna bez obzira na usitnjavanje lukova.
Dakle zakrivljenost ne teži ka nuli niti bilo kakvoj drugoj zakrivljenosti. Ali mi ipak kažemo da možemo
"ispeglati" kružnicu da bude duž koja nema zakrivljenost. Kako to možemo učiniti kad takve težnje
nema ma koliko usitnjavali lukove? Kad rezimiramo ispada sledeće: Imamo dve jednake duži od kojih
jedna nema zakrivljenost a druga u svakoj tački ima konstantnu zakrivljenost?
A sad nešto drugo - zašto bi neko povodom iznetog problema odgovarao srdito, uvredljivo ili na
način koji ništa ne objašnjava umesto da da svoje mišljenje, eventualno i svoju dilemu ili rešenje. [ mokelet @ 06.05.2009. 11:09 ] @
Citat: galet@world:A evo i problema koji izgleda jednostavan, ali kad se malo udubiš onda nije:
Kako izračunati dužinu kružnice?
Ako kružnicu podeliš na delove odnosno lukove i te lukove poređaš na neku pravu liniju tako da
se tetive tih lukova poklapaju s tom linijom onda dobijaš aproksimaciju dužine kružnice sabirajući
dužine tetiva. Što više usitnjavaš lukove dobijaš sve bolju aproksimaciju. Kada dužine tetiva teže
nuli onda sume sve sitnijih tetiva teže nekoj graničnoj vrednosti. I onda mi kažemo da je dužina
kružnice jednaka dužini neke prave duži, međutim, ako kolonu poređanih lukova presečemo na bilo
kom mestu - na tom mestu postoji zakrivljenost koja je konstantna bez obzira na usitnjavanje lukova.
Dakle zakrivljenost ne teži ka nuli niti bilo kakvoj drugoj zakrivljenosti. Ali mi ipak kažemo da možemo
"ispeglati" kružnicu da bude duž koja nema zakrivljenost. Kako to možemo učiniti kad takve težnje
nema ma koliko usitnjavali lukove? Kad rezimiramo ispada sledeće: Imamo dve jednake duži od kojih
jedna nema zakrivljenost a druga u svakoj tački ima konstantnu zakrivljenost?
Opet iznosiš isto pitanje, samo u drugačijoj formi. Ljudi na ovom forumu su ti već zadovoljavajuće odgovorili na tvoje nedoumice.
Mislim da bi zato tema trebala da se lock-uje.
Do tada bih galet@world-u preporučio da se malo informiše. Evo par linkova:
Code:
http://sr.wikipedia.org/wiki/Ceo_broj
http://sh.wikipedia.org/wiki/Prirodan_broj
http://sh.wikipedia.org/wiki/Racionalan_broj
http://sh.wikipedia.org/wiki/Iracionalan_broj
http://sh.wikipedia.org/wiki/Realan_broj
http://sh.wikipedia.org/wiki/Kompleksan_broj
http://sh.wikipedia.org/wiki/Beskonačnost
http://sr.wikipedia.org/sr-el/Kardinalnost
http://sh.wikipedia.org/wiki/Matematička_analiza
http://sr.wikipedia.org/sr-el/Metrički_prostor
http://sr.wikipedia.org/sr-el/Metrika_(matematika)
http://sr.wikipedia.org/sr-el/Tačka_(geometrija)
http://sr.wikipedia.org/sr-el/Prava
http://sr.wikipedia.org/sr-el/Duž
http://sr.wikipedia.org/sr-el/Ravan
http://sr.wikipedia.org/sr-el/Hilbertove_aksiome
http://sr.wikipedia.org/sr-el/Krug
http://sr.wikipedia.org/sr-el/Odnos_obima_i_prečnika_kruga
http://sr.wikipedia.org/sr-el/Pi
Itd.
[ Nedeljko @ 06.05.2009. 13:11 ] @
Zanimljivo je da fer raspravu traži neko čije je "diskutovanje" na granici drskosti i bezobrazluka.
Citat: galet@world: Ako je neko doveden u logički škripac ne razumevajući postojanost odnosa u konačnim i beskonačnim domenima onda naravno ne može ni da kaže ništa drugo osim onog što je naučio i to bez razumevanja. Opsednutost raznim teorijama, problematičnim aksiomima, teoremama i ko zna čime još je van svake sumnje kočnica i prepreka za nova otkrića.
Stoga mi ne pada napamet da ih proučavam pogotovu stoga što njihovi poznavaoci ne mogu dati adekvatan odgovor na jednostavna pitanja ili se na ovaj ili onaj način sujetno suprotstavljaju rešenjima za koja znaju da su tačna.
Niko ti ne brani da lupaš koliko hoćeš. Ako ti javno etiketiranje drugih predstavlja ličnu satisfakciju, OK, ali ako ti je cilj da nekoga u nešto ubediš, to na ovaj našin nećeš postići.
Da bi se vodila fer rasprava o bilo čemu, diskutanti moraju prihvatiti opšta pravila argumentovane diskusije. Ti konkretno tumačiš iskaze (kao što je 0+0=0) van konteksta u kome su formulisani i proglašavaš ih netačnim, što je vrlo fer u diskusiji.
Citat: holononi: Da li se neko seća "Makedonskog algoritma" za odredjivanje korena, kako su autori tvrdili "nerešivih jednačina" i to za samo nekoliko minuta olovkom. Članci o dvojici matematičara su izašli u časopisu "Računari u vašoj kući" pre 20 i kusur godina. Zanim me kako se završila ta priča.
Hilbert je kao deseti problem postavio pronalaženje opšteg algoritma za rešavanje diofantovskih jednačina, da bi Matijaševiš dokazao da čak ni utvrživanje da li data diofantovska jednačina ima ili nema rešenje nije algoritamski rešivo.
Konkretno, to znači da nije moguće sastaviti algoritam koji na ulazi prihvata proizvoljan konačan izraz u kome učestvuju operacije sabiranja oduzimanja i množenja, proizvoljan broj promenljivih i celobrojne konstante, a na izlazu daje odgovor da/ne na pitanje da li se te promenljive mogu zameniti celim brojevima, tako da vrednost izraza bude 0.
Makedonci su sa druge strane sastavili algoritam koji za proizvoljan takav izraz na ulazu i datu ograničenu oblast računali realna rešenja, za šta su odavno postojali numerički algoritmi. Skrenuo im je na to pažnju neki akademik JAZU, ali su oni nastavili sa svojim ("nećemo odati formulu" itd. Jedino se nisu izjasnili šta hoće i na osnovu čega.). Pre možda tri godine su dolazili kod profesora Slaviše Prešića (i verovatno drugih matematičara) sa željom da budu predloženi za Abelovu nagradu. Kada je profesor Prešić pitao gosta kako algoritam radi na primeru jednačine x 2-2=0, dobio je odgovor "nisam se spremio". Kasnije su nešto i demonstrirali, ali to nije odgovaralo formulaciji onoga za šta je Matijaševič dokazao da je algoritamski nerešivo.
[ holononi @ 06.05.2009. 13:20 ] @
Termin "zakrivljenost" se koristi u starijoj literaturi. Pogledati na primer
Apsen, "Repetitorij više matematike", II dio, Tehnička knjiga, Zagreb, 1964., str. 34.
Tu je dato da je zakrivljenost kružnice polumjera r data kao 1/r i naglašeno je da je zakrivljenost konstanta. U novijoj literaturi se koristi termin krivina krive i definiše se nešto strože pomoću limesa ili izvoda. Ali se suštinski svodi na 1/r. Pogledati na primer
Adnadjević, Kadelburg, "Matematička analiza II" treće izdanje, Nauka, Beograd, 1999., str 100.
ili
Lazarević, "Višedimenzionalna matematička analiza 1", Orion art, Beograd 2003., str. 314.
ili dato nešto jednostavnije u
Mihailović, Janić, "Elementi matematičke analize I", Naučna knjiga, Beograd, 1990., str. 308.
Problem dužine krive se rešava aproksimacijom pomoću upisanih i opisanih mnogouglova, što je već napomenulo više diskutanata na ovom forumu. Razlika je samo u tome što se u prvom slučaju govori o supremumu a u drugom slučaju o infimumu. Kako je LIMES jedini ispravan aparat u matematici za rukovanje beskonačno malim i beskonačno velikim veličinama to se isti primenjuje i u ovakvim slučajevima. Limes i njegovi sledbenici, izvod i integral su omogućili izvodjenje stavova o objektima koji se ne mogu predstaviti "opipljivim" sredstvima. Da su tako izvedeni zaključci ispravni pokazuje se u praksi svakodnevno,
Na primer, pri odredjivanju broja binarnih sudara molekula gasa, odgovarajućim transformacijama na polarne koordinate, dobije se da je  . Ovde je element zapremine predstavljen proizvodom dve beskonačno male veličine, gde su dx i dy priraštaji vektora brzine c.
Za detalje pogledati
Yeremin, "The Foundations of Chemical Kinetics", Mir publishers, Moscow, 1979., str. 158.
Rešenje pomenutog problema ima svoj ekvivalent poznat svakom srednješkolcu kao uticaj temperature na brzinu hemijske reakcije. Pogledati na primer
Rakočević, Horvat, "Opšta hemija za I razred srednje škole", Zavod za izdavanje udžbenika i nastavna sredstva, Beograd, 2006., str. 86.
Takodje, u istom udžbeniku su navedeni praktični ogledi kojima učenik može da proveri ponešto od opisanih pojava. Ovim je pokazan primer "svodjenja apstraktnog na konkretno". Neopipljivi pojmovi beskonačno malih veličina su našli svoju potvrdu u materijalnim eksperimenima, dostupnim svima na proveru. Ovo je takodje i osvrt na primedbu "ne može ni da kaže ništa drugo osim onog što je naučio i to bez razumevanja". Jer, pod razumevanjem se smatra da učenik ume da povezuje različite oblasti iste discipline a ovde je učinjeno više pa su povezane oblasti iz različitih disciplina.
Prema tome, svaka nova teorija, koja treba da pobije nešto od postojećih, moraće da dobro pripazi da ne dodje u koliziju sa raznim pojavnim oblicima danas važećih terija (koje nisu proizvod pukog maštanja, već rezultat rada velikog broja istraživača ne samo kroz prostor već i tokom vremena). Sve te teorije se dopunjuju i doradjuju u skladu sa novospoznatim istinama. U tom smislu "rušenje" postojećih definicija u matematici predstavlja "borbu sa vetrenjačama".
[ galet@world @ 06.05.2009. 13:22 ] @
Citat: Nedeljko: Zanimljivo je da fer raspravu traži neko čije je "diskutovanje" na granici drskosti i bezobrazluka.
Samo i isključivo kao odgovor na drskost i bezobrazluk. [ galet@world @ 06.05.2009. 13:53 ] @
Citat: holononi:U tom smislu "rušenje" postojećih definicija u matematici predstavlja "borbu sa vetrenjačama".
Nije rušenje nego dodatak.
[ holononi @ 06.05.2009. 19:40 ] @
Citat: Pre možda tri godine su dolazili kod profesora Slaviše Prešića (i verovatno drugih matematičara) sa željom da budu predloženi za Abelovu nagradu.
Interesantno.
Pomenuti autori su navodno očas rešili x4 + 7x3 - 2x2 + F*x + 2F - 344 = 0. Ovaj primer se može rešiti raznim metodama tako što se F prikaže kao kompleksni polinom. Medjutim da li je poznat primer jednačine koji je rešen "makedonskim algoritmom" a nije rešen drugim metodama. Takodje, interesantno je pitanje da li se "makedonskim algoritmom" brže stiže do rešenja ili se samo radi o veštini autora. Ko je uopšte, osim autora, video taj algoritam ?
[ Nedeljko @ 06.05.2009. 20:48 ] @
Citat: galet@world: Samo i isključivo kao odgovor na drskost i bezobrazluk.
Jok vala. Tu spada i tvrdoglavo i uporno tumačenje iskaza van konteksta u kome su formulisani.
Što se krivine tiče:
Ono što si napisao za obim kruga jeste primena definicije dužine krive na slučaj kada je ta kriva luk. To je jednostavno definicija dužine svidela se tebi ili ne. Ta definicija je korektna jer svakoj krivoj pridružuje tačno jednu vrednost iz intervala  . Iz tog razloga možemo uvesti i koristiti taj pojam.
Ako takav pojam dužine ne odgovara tvojim potrebama, onda uvedeš drugu definiciju i uvedenom pojmu daš neko novo ime, recimo G-dužina (od Galet), i uvedeš novu oznaku za nju (recimo  ). No, ako tvoj pojam bude imao različite osobine od standardnog pojma dužine, to ne potkopava nijedan od ta dva pojma. To su jednostavno različiti pojmovi za koje je normalno da imaju različite osobine. Takođe, ne možeš koristiti osobine jednog pojma za drugi pojam, niti tumačiti iskaze u kojima učestvuje standardan pojam dužine van konteksta u kome su formulisani, a koji je određen definicijama koje prethode tom stavu, što inače stalno radiš ovde sa nulom.
Što se borbe sa vertrenjačama tiče, ovo bi pre nazvao drugim imenima. [ galet@world @ 06.05.2009. 21:39 ] @
Citat: Nedeljko: Jok vala. Tu spada i tvrdoglavo i uporno tumačenje iskaza van konteksta u kome su formulisani.
Ovo su bila samo pitanja:
Citat: galet@world: Ali mi ipak kažemo da možemo "ispeglati" kružnicu da bude duž
koja nema zakrivljenost. Kako to možemo učiniti kad takve težnje nema ma koliko usitnjavali lukove? Kad
rezimiramo ispada sledeće: Imamo dve jednake duži od kojih jedna nema zakrivljenost a druga u svakoj
tački ima konstantnu zakrivljenost?
Ako nisi razumeo onda te podsećam da sam lukove stavio u kolonu na pravu liniju tako da im tetive leže na njoj
Nauči se da odgovaraš na pitanja - ako znaš - u protivnom tvoji tekstovi spadaju pod već datu kvalifikaciju.
[Ovu poruku je menjao galet@world dana 06.05.2009. u 22:55 GMT+1][ Fitopatolog @ 06.05.2009. 21:54 ] @
Dane, koliko je široka tvoja dnevna soba?
a) Mereno kao dužina duži
b) Mereno kao dužina luka (dela kružnice Zemljinog obima)
Kolika je širina pločice na podu u tvom kupatilu:
a) Kao duži
b) Kao luka
?
Kolika je dužina mrava koji šeta po podu tvoje kuhinje:
a) kao duži
b) kao luka
?
Da li možeš da proceniš kolika dužina štapa ti treba da bi izmerio sa njim obim Zemlje a da greška bude najviše 1%? Koliki treba da je štap da greška buda najviše 5%?
[Ovu poruku je menjao Fitopatolog dana 06.05.2009. u 23:34 GMT+1]
[ holononi @ 06.05.2009. 22:23 ] @
Kad baš teramo mak na konac, neka nam autor sledećeg citata objasni
Citat: Ja tvrdim da je 0 + 0 + 0 = 3•0
kako je dobio 3 od sve samih nula?
Citat: Ali mi ipak kažemo da možemo "ispeglati" kružnicu da bude duž koja nema zakrivljenost.
Autor ovog citata kaže "mi". Neka se jave svi ti "mi".
Ovde se može primetiti oblik onog što se naziva "zamena teza". Naime, diskutant povremeno zamenjuju objekat sa njegovom osobinom. Svaki objekat može da ima više osobina, kao i što odredjenu osobinu mogu da poseduju različiti objekti. U ovom slučaju objekti su kružnica i duž koja nema zakrivljenost. Oba ova objekta imaju više osobina. Jedna od osobina oba ova objekta je dužina. Medjutim, čak i kad imaju istu dužinu ovi objekti nisu isti. Time što smo na neki način odredili dužinu kružnice nismo je pretvorili u nešto drugo. Kružnica je i dalje kružnica a duž duž.
[ mokelet @ 06.05.2009. 22:56 ] @
Citat: holononi: Kad baš teramo mak na konac, neka nam autor sledećeg citata objasni
Citat: Ja tvrdim da je 0 + 0 + 0 = 3•0
kako je dobio 3 od sve samih nula?
Možda je mislio na konstrukciju skupa prirodnih brojeva:
0 = {}
1 = {0} = {{}}
2 = {0, 1} = {0, {0}} = {{}, {{}}}
3 = {0, 1, 2} = {0, {0}, {0, {0}}} = {{}, {{}}, {{}, {{}}}}
itd.
:-)
[ holononi @ 07.05.2009. 00:25 ] @
Citat: Možda je mislio na konstrukciju skupa prirodnih brojeva:
Jasno mi je šta ti misliš, ali s tobom se ništa ne sporimo.
[ mokelet @ 07.05.2009. 02:19 ] @
Citat: holononi: Jasno mi je šta ti misliš, ali s tobom se ništa ne sporimo.
Ma znam, nego pomažem da shvatiš šta je galet@world (nehotice) hteo da kaže. :-) [ galet@world @ 07.05.2009. 07:56 ] @
@ Fitopatolog
Sve te dužine ja merim kao tetive, a lukove možeš i sam da izračunaš
Citat: holononi: kako je dobio 3 od sve samih nula?
Evo ovako:
Računao sam odnose između tetiva kružnica od kojih jedna ima radijus 1 m a druga 3 m pa sam dobio
(gle čuda) za ugao od 30 0, (isti u obe kružnice) nasuprot tetiva da je odnos između tih
tetiva 1 : 3 - a ovo znači da je tetiva veće kružnice triput veća od tetive manje kružnice. Posle
toga nisam više računao tetive u većim kružnicama nego samo u manjim (koja drskost!) pa sam, da bi
dobio dužine većih tetiva, množio manje tetive sa 3. I, na kraju, drznuo sam se da to uradim čak i sa
graničnim tetivama koje imaju dužinu 0 ali ne 0 bez dimenzije pošto te tetive postoje
Što se tiče teranja maka na konac - čudi me kako to može neko da kaže - pa matematika je, valjda,
upravo takva nauka.
Citat: mokelet: Ma znam, nego pomažem da shvatiš šta je galet@world (nehotice) hteo da kaže. :-)
To nisam hteo da kažem ni hotimično ni nehotice jer ti govoriš o nepostojanju. Da ne bi bilo zabune
od sada ću nulu koja je definisana t. j. koja se dobija oduzimanjem dveju jednakih veličina, koja nema
dimenziju i koja označava nepostojanje zvati apsolutna nula jer ona to i jeste pošto
nema predznak, a nulu koja ima dimenziju t. j. koja postoji (egzistira) zvaću eg zistencijalna nula[ holononi @ 07.05.2009. 09:18 ] @
Citat: Evo ovako: Računao sam ...
Ovako opisan račun nije zasnovan na pravilima važećim u matematici budući da sadrži problematične konstrukcije. Jer kad bi čak i pronašli dve susedne tačke u skupu realnih brojeva, rastojanje izmedju njih ne bi bilo jednako 0. To sledi iz pravila d(x,y)=0 <=> x=y. Kako d(x,y)≥0 tada za d(x,y)>0 mora važiti x<>y. A ako x=y tada se ne radi ni o kakvoj novokomponovanoj "graničnoj tetivi" već o tangenti za koju znaju svi srednješkolci.
Ukoliko autor spornog citata i dalje tvrdi da je 0 + 0 + 0 = 3•0 <> 0, neka navede pravila za računanje u takvom sistemu. Na primer, bilo bi interesantno videti da li navedena struktura zadovoljava asocijativnost, komutativnost, distributivnost i slične osobine koje se ispituju pri oceni konzistentnosti algebrske strukture. Moguće je da je takva struktura izomorfna sa nekom od ranije poznatom strukturom a da mi to nismo uočili.
[ zzzz @ 07.05.2009. 10:28 ] @
Dane: Da ne bi bilo zabune
od sada ću nulu koja je definisana t. j. koja se dobija oduzimanjem dveju jednakih veličina, koja nema
dimenziju i koja označava nepostojanje zvati apsolutna nula jer ona to i jeste pošto
nema predznak, a nulu koja ima dimenziju t. j. koja postoji (egzistira) zvaću egzistencijalna nula.
Broj koji ima dimenziju???Zar broj nije apstraktan pojam, nekakav omjer istih
dimenzija, ako već voliš spomenuti dimenzije.
Znači li da po tvojoj teoriji 5 metara ili recimo 8 eura su "egzistencijalni" prirodni brojevi, dok su 5 i 8 apsolutni prirodni brojevi "jer
oni to i jesu pošto nemaju predznak".
Može li se teorija koju zastupaš nazvati Teorija o egzistencijalnim brojevima koji su bitno drukčijih i neobičnijih osobina od ovih apstraktnih?Naprimjer tu bi imali pravilo
da 2+2 nije uvijek 4.Operacija + vrijedi samo u rijetkim slučajevima, jer se ne mogu sabirati babe i žabe.
Možeš li ovo malo pojasniti jer možda sam krivo ukapirao.
[ Nedeljko @ 07.05.2009. 10:55 ] @
Citat: galet@world: Da ne bi bilo zabune od sada ću nulu koja je definisana t. j. koja se dobija oduzimanjem dveju jednakih veličina, koja nema dimenziju i koja označava nepostojanje zvati apsolutna nula jer ona to i jeste pošto nema predznak, a nulu koja ima dimenziju t. j. koja postoji (egzistira) zvaću eg zistencijalna nula
Ovo je već bolje. Međutim, nema nikakve potrebe izmišljati novu terminlogiju za pojmove koji odavno imaju imena. Neutral za sabiranje se zove nula, a ono na šta pretenduješ sa "egzistencijalnom nulom" se već zove infinitezimala. No, pojam polja realnih brojeva takođe ima precizno definisano značenje i u tom polju nema infinitezimala. Da bi radio sa beskonačno bliskim vrednostima, moraš odustati od polja realnih brojeva. Račun sa infinitezimalam već postoji, ali u drugim poljima. Nije nikakav problem da definišeš neku svoju strukturu i nazoveš je G-struktura. No, ta struktura nećs "oboriti" strukturu polja realnih brojeva. [ realan @ 07.05.2009. 14:55 ] @
Znači kružnica je ustvari jedan trapez...
[ holononi @ 07.05.2009. 15:26 ] @
Mathematica s zalut de
Def: Korpa je mreža koja nema dno.
Def: Mreža koja nema dno je pacov bez rogova.
Def: Pacov bez rogova je oblak medju kukuruzima.
Def: Oblak medju kukuruzima je parcijalno rekurzivan tramvaj.
Def: Parcijalno rekurzivan tramvaj je avion koji zadovoljava sledeće uslove:
- tramvaj je
- ne pliva
- nema brkova.
Def: Avion koji nema brkova je sova.
T:  Sova je na staklenim nogama.
Dokaz: Dokaz ne sledi iz toga što je pao avion, već u koliko sati doručkuju krokodili. Tačan odgovor je pacov i samo pacov pod rogovima.
Srdačno, Vaš
Kapriciozo
PS. 21 * 31 = 651 jer je 1 * 1 = 1 QED
[ Nedeljko @ 07.05.2009. 17:32 ] @
Citat: galet@world: Računao sam odnose između tetiva kružnica od kojih jedna ima radijus 1 m a druga 3 m pa sam dobio (gle čuda) za ugao od 300, (isti u obe kružnice) nasuprot tetiva da je odnos između tih tetiva 1 : 3 - a ovo znači da je tetiva veće kružnice triput veća od tetive manje kružnice. Posle toga nisam više računao tetive u većim kružnicama nego samo u manjim (koja drskost!) pa sam, da bi dobio dužine većih tetiva, množio manje tetive sa 3. I, na kraju, drznuo sam se da to uradim čak i sa
graničnim tetivama koje imaju dužinu 0 ali ne 0 bez dimenzije pošto te tetive postoje
I šta je na kraju definicija granične tetive? Nemoj samo da mi pominješ "poslednji trenutak pre..." jer takav trenutak ne postoji - između svaka dva trenutka postoji beskonačno mnogo trenutaka. [ Cabo @ 07.05.2009. 17:35 ] @
Čini mi se da je galet već postavljao slične teme, kao što reče neko u ovoj temi. Moja poruka za njega, kao i tamo, je da prouči pojam beskonačnosti i njegov odnos sa konačnim veličinama. To je osnova oblasti koja se zove Račun ( Calculus) a sastoji se od Matematičke analize, Diferencijalnog računa, itd.
galet, kada budeš stvarno shvatio pojam, recimo, skupa mere nula, kao i to da je ceo skup  svih racionalnih brojeva mere nula, svih racionalnih brojeva mere nula, ili značenje reči „prebrojivo“ i „neprebrojivo“, kao i, recimo, zašto je  , onda se javi pa da pričamo.
P.S.: Našao sam temu i moju poruku u njoj: http://www.elitesecurity.org/p2179442
Sve se u suštini vrti oko fundamentalnog nerazumevanja pojma tačke (koja je nedeljivi, ali istovremeno i postojeći, apstraktni objekat) i broja (koji je konačna veličina), kao i toga da ne postoji „broj  “, već je to samo poštapalica za kraći zapis formula.
[Ovu poruku je menjao Cabo dana 07.05.2009. u 22:33 GMT+1][ galet@world @ 07.05.2009. 22:42 ] @
Citat: holononi: A ako x=y tada se ne radi ni o kakvoj novokomponovanoj "graničnoj tetivi" već o tangenti za koju znaju svi srednješkolci.
Svi srednjoškolci znaju da tetiva nije tangenta, ali što da uznemiravamo tako visoko obrazovan kadar kad svaka
nepismena baba zna da njiva i međa nisu isto.
Citat: zzzz:Možeš li ovo malo pojasniti jer možda sam krivo ukapirao.
Ide jedan čovek jednom stranom ulice i viče: "Koliko". Svi ćute, ali se ipak našao jedan na drugoj strani ulice
koji mu odgovori: "Pet", a onda onaj što je vikao upita: " Šta pet", o onaj drugi mu odgovori pitanjem:
"A šta koliko"
Citat: Nedeljko: Ovo je već bolje. Međutim, nema nikakve potrebe izmišljati novu terminlogiju za pojmove koji odavno imaju imena. Neutral za sabiranje se zove nula, a ono na šta pretenduješ sa "egzistencijalnom nulom" se već zove infinitezimala. .... No, ta struktura nećs "oboriti" strukturu polja realnih brojeva.
To mi nije ni bila namera. A ti bi mogao da baš u tom smislu koriguješ ovaj svoj biser: 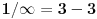
Kad bi morao da odgovoriš gde je infinitezimala, šta bi rekao na kojoj strani se nalazi - levoj ili desnoj ovog izraza.
Citat: Nedeljko: I šta je na kraju definicija granične tetive? Nemoj samo da mi pominješ "poslednji trenutak pre..." jer takav trenutak ne postoji - između svaka dva trenutka postoji beskonačno mnogo trenutaka.
Ona nepismena baba zna da je njiva u kontaktu sa međom.
Citat: Nemoj samo da mi pominješ "poslednji trenutak pre..." jer takav trenutak ....
I neću za apsolutnu nulu, ali za egzistencijalnu moram.
Citat: Cabo: Moja poruka za njega, kao i tamo, je da prouči pojam beskonačnosti ...
Bolje i lakše bi mi bilo da mi ti to ispričaš ukratko. Usput da te pitam kad si već tu za tvoje mišljenje o ovoj ideji:
Zamislimo neku kružnicu kao jedinicu mere za sve ostale kružnice - dakle neku mernu jediničnu kružnicu i
onda da ostale kružnice izražavamo pomoću nje - ne bi nam trebao ni broj pi ni pretvaranje kružnice u ono što nije.
Ne bi morali meriti jednu pojavu pomoću druge jer to ne ide baš lako. [ holononi @ 07.05.2009. 23:01 ] @
Citat: dakle neku mernu jediničnu kružnicu i onda da ostale kružnice izražavamo pomoću nje - ne bi nam trebao ni broj pi ni pretvaranje kružnice u ono što nije
Naravno da smo mogli, samo onda bi tumarali za jedinicom k'o ćorave koke.
Citat: Kad bi morao da odgovoriš gde je infinitezimala, šta bi rekao na kojoj strani se nalazi - levoj ili desnoj ovog izraza.
Na ovo pitanje je dat odgovor više puta.
[ Farenhajt @ 07.05.2009. 23:19 ] @
Ja ću opet ponoviti svoje pitanje od pre neki dan, ali bih ovog puta voleo da čujem nekoga od "potrošača" ove teme:
U čemu je čar preganjanja s Gaćešom? Opšta zaludnost? Ili možda iluzorna nada da se tu IPAK može iščačkati neka teorija? (LOL^2\cdot ROFL^3)
Zbilja mi je teško da poverujem da ovde redovni diskutanti nemaju pametnije da utroše 10-15 minuta, koliko im treba da pročitaju nove poruke i sroče odgovor. Kad bi neko došao i uzeo da dokazuje da je 2+2=4 loše definisano i da tu treba temeljna prerada u 2+2 & 4, gde znak "&" označava novu matematičku relaciju "mož' da bidne al' ne mora da znači, zavisi jel' egzistencijalno il' apsolutno", da li biste trošili ikakvo vreme i reči na njega? Jeste, ovde se barata poljem realnih brojeva, koje je daleko "ozbiljnije" od računice za prvi osnovne, ali je princip, gospodo, zbilja isti.
Dakle, zanima me da čujem ZAŠTO gostujete ovde. Iz dana u dan.
[ holononi @ 08.05.2009. 00:46 ] @
Citat: Dakle, zanima me da čujem ZAŠTO gostujete ovde. Iz dana u dan.
Iz prostog razloga jer je ovo čisto teorijska tema, Rešavanje praktičnog zadatka se završava onda kad neko reši zadatak i takav forum se ugasi. Ovde, pak možete sebe preslišavati kakve odgovore bi uputili učenicima koji izbegavaju da uče a ipak tu i tamo po nešto znaju. Jer, iskreno govoreći uvek može da se otvori polmika "šta je to tačka", "šta je prava", "šta je ravan". Kako ćete odgovoriti na to? Hilbertovski "to nećemo ni definisati"? Kao što je već napomenuto ove postove će čitati i neko drugi osim nas. Možda mu zatreba osvrt na to kako se pristupa matematici. U tom cilju smo na neki način i primorani da odgovorimo na izjave koje su za matematičare "obična nebuloza". Ako niko ne bi reagovao, neko ko se tek uči mogao bi izvući pogrešan zaključak. Pokušaj usmeravanja diskusije u drugim pravcima nije davao trajnijeg efekta.
[ Farenhajt @ 08.05.2009. 01:21 ] @
Citat: holononi: Iz prostog razloga jer je ovo čisto teorijska tema, Rešavanje praktičnog zadatka se završava onda kad neko reši zadatak i takav forum se ugasi. Ovde, pak možete sebe preslišavati kakve odgovore bi uputili učenicima koji izbegavaju da uče a ipak tu i tamo po nešto znaju. Jer, iskreno govoreći uvek može da se otvori polmika "šta je to tačka", "šta je prava", "šta je ravan". Kako ćete odgovoriti na to? Hilbertovski "to nećemo ni definisati"? Kao što je već napomenuto ove postove će čitati i neko drugi osim nas. Možda mu zatreba osvrt na to kako se pristupa matematici. U tom cilju smo na neki način i primorani da odgovorimo na izjave koje su za matematičare "obična nebuloza". Ako niko ne bi reagovao, neko ko se tek uči mogao bi izvući pogrešan zaključak. Pokušaj usmeravanja diskusije u drugim pravcima nije davao trajnijeg efekta.
Hm... Ako je cilj predočiti neke elementarne pojmove - a ako ti se ne sviđa Hilbertova granica, slobodno možeš postaviti neku svoju, ali na kraju ćeš završiti s ovim ili onim skupom pojmova koje NE MOŽEŠ definisati nego ih moraš aksiomatski uzeti (npr. ako definišeš prirodni broj, onda aksiomatiziraš skup), te na pitanje "šta je tačka" ionako nikad nećeš imati sasvim dobar odgovor - onda je daleko delotvornije otvarati "priručničke" teme, sa sažecima aksiomatike pojedinih grana matematike, nego očekivati da će iko naći "zrnce zlata" u temi koja se bavi ISKLJUČIVO akanjem s jednim jedinim korisnikom foruma. A što se tiče mogućnosti sticanja "pogrešnog utiska", nešto ne vidim da bi se to moglo desiti u temi gde pomenuti korisnik stalno postavlja pitanja, ali mu niko ne odgovara. Ili mu odgovara moderator porukom kojom ga upućuje na odgovarajuću temu iz aksiomatike, a potom zaključa temu.
Inače, kad te neko pita "šta je prava", "šta je ravan", najbolje je reći mu "prava je ravan"... (pa ga pošalješ da dokaže postojanje bijekcije između prave i ravni). [ galet@world @ 08.05.2009. 08:03 ] @
Citat: holononi:Naravno da smo mogli, samo onda bi tumarali za jedinicom k'o ćorave koke.
Da, tako je. Na primer za svaku elipsu drugog ekscentriciteta morali bi imati jediničnu elipsu - ideja ne dolazi u obzir.
Citat: Na ovo pitanje je dat odgovor više puta.
Ali nije dat odgovor šta tu radi znak jednakosti.
Citat: Farenhajt: U čemu je čar preganjanja s Gaćešom?
Neko nalazi čar u razmišljanju, a neko u već pomenutom primitivizmu. [ holononi @ 08.05.2009. 08:57 ] @
Citat: Ali nije dat odgovor šta tu radi znak jednakosti.
Ukoliko je kontekst diskutabilan, uvek se mogu koristiti strelice.
Citat: kad te neko pita "šta je prava", "šta je ravan", najbolje je reći mu "prava je ravan"...
Da li baš? A šta ako on nakon što uspostavi bijekciju izmedju prave i ravni doda još jednu ravan pa dokaže da i tu postoji bijekcija, pa sledeću ravan, pa sledeću i tako pokupi ceo prostor? Da li bi tu upali u zamku da dokazujemo sve i svašta svim i svačim?
[ Farenhajt @ 08.05.2009. 09:12 ] @
Citat: holononi: Da li baš? A šta ako on nakon što uspostavi bijekciju izmedju prave i ravni doda još jednu ravan pa dokaže da i tu postoji bijekcija, pa sledeću ravan, pa sledeću i tako pokupi ceo prostor? Da li bi tu upali u zamku da dokazujemo sve i svašta svim i svačim?
Zapravo bi tu bilo zanimljivo videti u šta se npr. kompletna geometrija trougla pretvara ako ravan bijektivno preslikaš na pravu. (A pod "u šta" podrazumevam "u poređenju sa 'zdravorazumskom' geometrijom prave". Da li tom operacijom prava postaje "svuda prekidna i svuda neuređena"?)
(Što se onog gore tiče: što bi toliko komplikovao? Dosta mu je da direktno bijektivno preslika čitav prostor na pravu...) A u zamku ne možemo upasti jer, koliko znam, u višedimenzionalnim skupovima tačaka ne možeš ostvariti potpuno uređenje, kakvo možeš u jednodimenzionalnom skupu, tako da problem "sve i svašta svim i svačim" ne postoji.
Dakle, prava bi se kao skup tačaka mogla dovesti u tesnu vezu s potpuno uređenim poljem realnih brojeva. Ravan bi se takođe povezala s realnim brojevima, ali bez uređenosti. Kako bi se onda okarakterisao prostor?
Ima tu još (bar meni) zanimljivih pitanja:
1. Može li se uspostaviti bijekcija između tačaka jedne prave i pravih jedne ravni?
2. Ako može, da li se tom bijekcijom može očuvati uređenost? Tj. da li je skup pravih jedne ravni izomorfan polju realnih brojeva?
[Ovu poruku je menjao Farenhajt dana 08.05.2009. u 10:28 GMT+1][ holononi @ 08.05.2009. 09:56 ] @
Citat: Dakle, prava bi se kao skup tačaka mogla dovesti u tesnu vezu s potpuno uređenim poljem realnih brojeva.
Ideja izgleda dosta dobro. Tačka u ravni bi se mogla definisati kao uredjen par (x,y) iz R 2, tačka u prostoru bi bila uredjena trojka (x,y,z) iz R 3 itd.
Citat: Tj. da li je skup pravih jedne ravni izomorfan polju realnih brojeva?
Ako bi se vratili na prethodno diskutovana pitanja u vezi rastojanja, tada bi se moglo postaviti pitanje šta je rastojanje dve prave? U skupu realnih brojeva smo to odredili, ali takve operacije nisu bijektivne. Odnosno, može se uspostaviti bijekcija ali samo na jednom delu realne prave.
[Ovu poruku je menjao holononi dana 08.05.2009. u 14:15 GMT+1][ Nedeljko @ 08.05.2009. 10:57 ] @
Citat: galet@world: To mi nije ni bila namera. A ti bi mogao da baš u tom smislu koriguješ ovaj svoj biser: 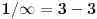
Šta da ti kažem, ta jednakost je posledica definicije oduzimanja realnih brojeva i definicije deljenja u proširenom skupu realnih brojeva, tako da nije "biser", već teorema.
Što se tiče infinitezimala, u toj strukturi ih nema. Kada se radi u nearhimedovskom poljima, onda ne postoji jedna oznaka za infinitezimalu, niti jedna za beskonačno veliku veličinu iz prostog razloga što ih ima beskonačno mnogo i ravnopravne su među sobom. Stoga ovaj zapis koji si upotrebio ne pripada tom računu, već računu u proširenom skupu realnih brojeva gde su operacije definisane tako kako su definisane. U nearhimedovskim poljima, bilo beskonačno malu, bilo beskonačno veliku veličinu možeš označiti bilo kojim slovom, s tim da u tekstu naglasiš kakva je koja veličina. [ galet@world @ 08.05.2009. 13:29 ] @
Citat: Nedeljko: Šta da ti kažem, ta jednakost je posledica definicije oduzimanja realnih brojeva i definicije deljenja u proširenom skupu realnih brojeva, tako da nije "biser", već teorema.
Ako je to teorema onda se izvinjavam što sam je pripisao tebi, ali čija god da je ona ne valja pa ne valja.
Kako da "prevedem" podvučene reči u citatu? [ miki069 @ 08.05.2009. 13:30 ] @
"Ako kružnicu posmatramo iznutra onda je ona konkavna, a ako je posmatramo spolja ona je konveksna..."
Za f(x) konveksnost/konkavnost je precizno definisana i skroz je obrnuto.
Ovo je napisano u otvaranju teme.
Što neko već napisa čitaće ovo i neka deca i smejaće se.
Predlažem Bojanu da klikne na LOCK
[ mokelet @ 08.05.2009. 13:50 ] @
Citat: galet@world: Ako je to teorema onda se izvinjavam što sam je pripisao tebi, ali čija god da je ona ne valja pa ne valja.
Ne znaš osnovne stvari u matematici? OK, niko se nije rodio sa znanjem.
Ne želiš da znaš osnovne stvari o matematici? OK, nije matematika centar sveta.
Sumnjaš u nešto, a pritom ne poseduješ dovoljno znanja? OK, sve može da se nauči.
Sumnjaš u nešto o čemu ne želiš da naučiš? Nije OK.
[ Nedeljko @ 08.05.2009. 13:52 ] @
Citat: galet@world: Ako je to teorema onda se izvinjavam što sam je pripisao tebi, ali čija god da je ona ne valja pa ne valja.
Kako to misliš da teorema može da ne valja? Ako je teorema, onda valja.
Po definiciji delenja u proširenom skupu realnih brojeva (dvema konstantama 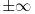 ) je 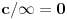 za ma koji realan broj  , a po definiciji oduzimanja u skupu realnih brojeva je 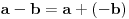 , gde je 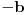 takav realan broj za koji je 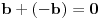 . Dakle, 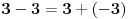 , a 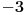 je po definiciji takav realan boj za koji je 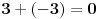 , pa je samim tim 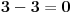 . Obzirom da je 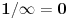 i 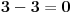 , važi 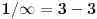 . Kraj dokaza.
Dakle, taj iskaz je itekako tačan u kontekstu u kome je formulisan, a tumačenja postojećih iskaza van konteksta u kome su formulisani neću da prihvatim i tačka. Novi iskazi su druga stvar. [ Cabo @ 08.05.2009. 15:00 ] @
Citat: galet@world: Bolje i lakše bi mi bilo da mi ti to ispričaš ukratko. Usput da te pitam kad si već tu za tvoje mišljenje o ovoj ideji:
Zamislimo neku kružnicu kao jedinicu mere za sve ostale kružnice - dakle neku mernu jediničnu kružnicu i
onda da ostale kružnice izražavamo pomoću nje - ne bi nam trebao ni broj pi ni pretvaranje kružnice u ono što nije.
Ne bi morali meriti jednu pojavu pomoću druge jer to ne ide baš lako. 
Slažem se sa predlogom za zaključavanje teme. +1.
(Uzgred, nije da ne bih mogao da uradim to što galet hoće, ali mislim da je posredi očigledna provokacija.) [ galet@world @ 08.05.2009. 20:08 ] @
Alal vera na dokazu!
Jedna prava dugačka je beskonačno mnogo kilometara. Ta ista prava dugačka je beskonačno mnogo metara.
Druga beskonačnost veća je od prve hiljadu puta. Kako se može govoriti o beskonačnosti kao o konstanti kad
pod pojmom beskonačnosti treba podrazumevati beskonačan skup različitih beskonačnosti?
Ako imaš 100 kg pšenice pa ti neko uzme tih 100 kg pšenice onda nemaš ništa, a to ništa je takvo
nepostojanje da se čak ne zna ni šta si imao.
Ako 100 kg pšenice podeliš na beskonačno dobićeš isto ništa, ali to ništa nije nepostojanje kao u prethodnom
slučaju jer se obrnutim postupkom t. j. množenjem tog ništa sa beskonačno opet dobija 100 kg pšenice.
U prvom slučaju od nepostojanja se ne može dobiti ništa bez obzira čime to ništa pomnožiš jer se ne zna ni
šta nemaš. To ništa je apsolutno jednako bez obzira na to šta si imao. Prema tome ni proizvod tog ništa i
beskonačnog broja ne može imati dimenziju, pogotovo zato što to ništa nije ni nastalo deljenjem.
Citat: mokelet: Ne znaš osnovne stvari u matematici?
Ti znaš pa odgovori, ali bez okolišanja i izvlačenja na tuđe neznanje.
Citat: miki069:Predlažem Bojanu da klikne na LOCK
Pa ustvari taj LOCK postoji od početka ove teme, jer jednako toliko sam dobio pravih i direktnih odgovora
na moja pitanja kao da je tema zaključana. To ne bi bila neka velika promena. [ Farenhajt @ 08.05.2009. 20:19 ] @
Citat: holononi: Ako bi se vratili na prethodno diskutovana pitanja u vezi rastojanja, tada bi se moglo postaviti pitanje šta je rastojanje dve prave? U skupu realnih brojeva smo to odredili, ali takve operacije nisu bijektivne. Odnosno, može se uspostaviti bijekcija ali samo na jednom delu realne prave.
Pa dakle, "zdravorazumsko" odstojanje dve prave (onakvo kakvo se definiše za, recimo, paralelne prave) ne bi funkcionisalo u svrhu izomorfizma. Ali da li se može SROČITI formula za računanje odstojanja koja bi bila saglasna s izomorfizmom? [ Nedeljko @ 09.05.2009. 12:52 ] @
Citat: galet@world: Alal vera na dokazu!
Jedna prava dugačka je beskonačno mnogo kilometara. Ta ista prava dugačka je beskonačno mnogo metara.
Druga beskonačnost veća je od prve hiljadu puta. Kako se može govoriti o beskonačnosti kao o konstanti kad
pod pojmom beskonačnosti treba podrazumevati beskonačan skup različitih beskonačnosti?
Ako imaš 100 kg pšenice pa ti neko uzme tih 100 kg pšenice onda nemaš ništa, a to ništa je takvo
nepostojanje da se čak ne zna ni šta si imao.
Ako 100 kg pšenice podeliš na beskonačno dobićeš isto ništa, ali to ništa nije nepostojanje kao u prethodnom
slučaju jer se obrnutim postupkom t. j. množenjem tog ništa sa beskonačno opet dobija 100 kg pšenice.
U prvom slučaju od nepostojanja se ne može dobiti ništa bez obzira čime to ništa pomnožiš jer se ne zna ni
šta nemaš. To ništa je apsolutno jednako bez obzira na to šta si imao. Prema tome ni proizvod tog ništa i
beskonačnog broja ne može imati dimenziju, pogotovo zato što to ništa nije ni nastalo deljenjem.
Dužina prave je ista konstanta, merio je u metrima ili milimetrima. Međutim, delenje beskonačnosti beskonačnošću nije definisano. Množenje bilo kojom vrednošžu osi nule je definisano i daje beskonačnost. U proširenom skupu realnih brojeva imaš tačno dve beskonačnosti, jednu pozitivnu i jednu negativnu.
Znači,
1000*dućina prave u metrima = dužina prave u milimetrima je tačno.
167*dućina prave u metrima = dužina prave u milimetrima je tačno.
10*dućina prave u metrima = dužina prave u metrima je tačno.
Dužina prave u metrima podeljena sa dužinom prave u metrima je nedefinisano.
Dužina prave u metrima podeljena sa dužinom prave u milimetrima je nedefinisano.
U ravni nad nearhimedovskim poljem postoji duž beskonačne dužine, koja je sadržana u nekoj još široj duži. Tamo je dužina takve duži beskonačno velika veličina i dobižeš da je dužina duži u milimetrima tačno 1000 puta veća od dužine duži u metrima - ni manje, ni više. E, to je sasvim drugi kontekst.
Što se pšenice tiče, zavisi kakva je raspodela pčenice u prostoru i kako se vrši delenje. Primera radi, ja mogu da izdvojim polovinu pšenice kao prvi deo. Drugi deo će mi biti polovina od preostale polovine. Treći deo će mi biti polovina od preostale četvrtine i tako dalje. n-ti deo će imati masu 100kg/2 n. I to je jedan od načina delenja pšenice na beskonačno mnogo delova, ali kod njega svaki deo ima veću masu od nule. [ holononi @ 09.05.2009. 15:11 ] @
Citat: Ali da li se može SROČITI formula za računanje odstojanja koja bi bila saglasna s izomorfizmom?
Ako sam te dobro razumeo, slažemo se da to ne može u opštem slučaju. Pa da se vratimo na polazni problem. Kako definisati osnovne pojmove tačke, prave i ravni a da ne dolazimo do kontraverzi. U terminima analitičke geometrije možda se i možemo pomoći uredjenim n-torkama. No, matematički aparat analitičke geometrije se ne koristi pri izvodjenju zaključaka u opštoj geometriji. Opšta geometrija se svodi na klasifikciju objekata u terminima poretka, odnosno pripadanja i rasporeda, i podudarnosti i neprekidnosi. Kako u takvim kategorijama pronaći osnov za valjano definisanje osnovnih geometrijskih pojmova?
Postoje u matematičkim krugovima oni koji smatraju da bi proučavanje matematike trebalo početi teorijom mere. Ako bi se takav stav prihvatio, tada bi se iznova morali definisati novi (stari) pojmovi. Tačka bi mogla da bude skup u prostoru R 1 Lebegove mere nula i kardinalnosti 1. Jel' to previše komplikovano?
Proveravam aksiome pripadanja:
1) Svaka prava sadrži najmanje dve RAZNE tačke.
Znam šta je tačka, ne moraju biti susedne. Ovo nije problem, ne postoji ni jedno epsilon > 0 tako da mogu izdvojiti prebrojiv skup intervala pa nema Lebegovu meru nula u prostoru R 1 a kardinalnosti je kontinuum. Sad znam i šta je prava.
2) Postoji najmanje jedna prava koja sadrži dve tačke.
Uh, dosta za danas.
[ Farenhajt @ 09.05.2009. 19:02 ] @
Citat: holononi: Ako sam te dobro razumeo, slažemo se da to ne može u opštem slučaju.
Nisam siguran da si me dobro razumeo. Tražim alternativnu definiciju.
Uostalom, kako Lobačevski definiše "odstojanje paralelnih pravih"?
A što se tiče ovog drugog dela tvoje poruke: Ne koristi se ni aparat polja realnih brojeva pri dokazivanju stvari u aritmetici (celih brojeva), pa to opet ne znači da celi brojevi nisu realni. Samo što to "prećutkuješ" mlađim uzrastima, a saopštiš starijima. [ galet@world @ 09.05.2009. 20:49 ] @
Citat: Nedeljko:
Dužina prave u metrima podeljena sa dužinom prave u metrima je nedefinisano.
Dužina prave u metrima podeljena sa dužinom prave u milimetrima je nedefinisano.
E sad se postavlja pitanje šta je deljenje. Ima vic. Pitali su jednog bezazlenog učenika koliko je pet podeljeno
na pet, a on je odgovorio - pet. Posle su ga da bi ga "urazumili" pitali - ako imaš pet jabuka pa ih podeliš na
pet drugara - koliko je to onda? On je opet odgovorio - pet. I zaista on realno razmišlja - sve su jabuke tu
negde i ima ih zaista pet. Niko ga nije pitao koliko jabuka dobija jedan drugar pa su njegovi odgovori
ustvari tačni. Pod deljenjem se takođe podrazumeva i usitnjavanje, ali podjednako. Naravno, podela nečega
se može izvršiti na razne načine i nejednako, ali ipak to se ne podrazumeva kod deljenja.
Ja ovde hoću da naglasim jednu izuzetno važnu osobinu brojeva - a to je održanje odnosa. Možda
to treba da se drukčije kaže, ali nadam se da je jasno o čemu se radi. Održanje odnosa je fantastično svojstvo
zato što nam ono daje informaciju o tome šta se dešava između beskonačno velikih i beskonačno malih
brojeva odnosno veličina ili kako se to već u matematici kaže. Svaka pojava je okarakterisana skupom
određenih odnosa koji je ustvari definišu - izostanak nekog od tih definišućih odnosa menja jednu pojavu u
drugu.
Problem kod beskonačno velikih i beskonačno malih veličina sastoji se u tome što bi trebalo odrediti
neku "jediničnu" egzistencijalnu nulu i neku "jediničnu" beskonačnost s kojima bi se druge takve veličine
upoređivale ako je to uopšte moguće. [ Nedeljko @ 10.05.2009. 13:21 ] @
Beskonačnost nije broj. To je samo pomoćno sredstvo u računanju limesa. Smisao jednakosti 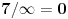 je da ako imaš dva realna niza, od kojih prvi teži ka 7, a drugi beskonačnosti, da onda njihov količnik teži nuli. Računanjem u proširenom skupu realnih brojeva se računaju neki limesi (kaže se još i limesi koji se računaju neposredno), kao na primer
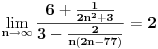 . [ holononi @ 10.05.2009. 15:12 ] @
Ovde se priča vic na račun matematičara (nemam ništa proiv toga i ja to ponekad radim) a onda se dodaje
"Možda to treba da se drukčije kaže, ali nadam se da je jasno o čemu se radi. "
Ne nije jasno o čemu se radi, jer meni ovo liči na MANIPULACIJE. Matematičari to ne rade. Kod matematičara se može čuti nešto poput "vidi se iz konteksta". Ali tu nema prevare. Ako nekom nije jasno to je njegov problem, tim pre ako ignoriše sva pozitivno data uputstva i sugestije a hoće da se upusti u tešku raspravu. Koristimo simbol R da označimo skup realnih BROJEVA. Kao što je već napisano u postu pre ovog, BESKONAČNO NIJE BROJ. Medjutim to beskonačno je potrebno pa se u matematici kaže "proširujemo skup realnih brojeva SIMBOLIMA  i  ". Tada je PROŠIREN skup realnih brojeva, 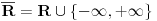 . U nastavku koristim istu oznaku za oba skupa bez opasnosti od zabune ako se vidi kontekst. Matemtičari jasno vide kontekst kad se predje na limes. I matematičarima je to potpuno jasno. Ako neko misli da treba da se rita sa potkovanima moraće i sam da se potkuje ili da "broji čvoruge". Kako je na ovom forumu dato dovoljno materijala za uvod onima koji se tek uče, sledi da diskusiju možemo podići na nivo kako matematičari diskutuju u ovakvim situacijama. U medjuvremenu, zainteresovani se mogu preslišati iz citiranih referenci, a ne da svoje neznanje pravdaju tobožnjim propustima nauke.
[ Cabo @ 10.05.2009. 16:23 ] @
Ova tema je još uvek otključana?! O_o
Citat: holononi:
Koristimo simbol R da označimo skup realnih BROJEVA. Kao što je već napisano u postu pre ovog, BESKONAČNO NIJE BROJ. Medjutim to beskonačno je potrebno pa se u matematici kaže "proširujemo skup realnih brojeva SIMBOLIMA  i 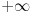 ". Tada je PROŠIREN skup realnih brojeva, 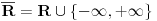 .
Kao što rekoh,  je samo način da se manje piše, to nije strogo formalno korektno definisan matematički objekat, jer treba dodefinisati operacije polja  kao što su  , a verovatno i još ponešto, što mi nije ovako „na prvu loptu“ palo na pamet.
Dodatak:
Da demonstriram: važi 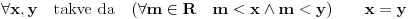 , jer je u suprotnom 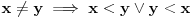 , što je u suprotnosti sa njihovom definicijom. Dakle,  je jedinstven „broj“ za svoju definiciju 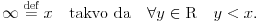
Takođe, 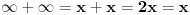 , jer bi inače 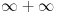 bio veći „broj“ od  , što je kontradikcija. To dalje znači da je „broj“  neka vrsta neutrala za sabiranje, koji je različit od nule, pa je 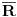 malkice malkice drugačija struktura od polja.
[Ovu poruku je menjao Cabo dana 10.05.2009. u 19:26 GMT+1][ galet@world @ 10.05.2009. 17:33 ] @
Neko traži spas u zaključavanju teme, a neko trabunja kao i da je doslovno potkovan.
Samo neko kom je više stalo do pukog formalizma a ne do istine može da kaže da se
100 kg pšenice može uništiti deljenjem.
[ Cabo @ 10.05.2009. 17:49 ] @
Citat: galet@world: Neko traži spas u zaključavanju teme, a neko trabunja kao i da je doslovno potkovan.
Samo neko kom je više stalo do pukog formalizma a ne do istine može da kaže da se
100 kg pšenice može uništiti deljenjem.
Da, upravo to je poenta „broja“  . On „jede“ konačne brojeve. Na sličan način na koji ih „jede“ neutral za sabiranje kada se na njega i konačan broj (100 kg pšenice) primeni množenje:  .
Po meni je naučna istina nešto što se može formalno dokazati aparatom matematičke logike. Sve ostalo je religija zasnovana na nekim delovima nauke („ja verujem/mislim/smatram uprkos formalnim dokazima“). [ holononi @ 10.05.2009. 18:52 ] @
Citat: Samo neko kom je više stalo do pukog formalizma
Do istine u matematici se dolazi strogim formalizamom. A od inventivnog matematičara se često zahteva da ono što postoji pronadje u nečem drugom što ne postoji. Ova osobina se redje razvija u drugim disciplinama pa se ponekad takve diskusije završe "razgovorom gluvih". Ne, definitivno se ne može sve objasniti, jedini lek je knjiga u šake uz poveće injekcije razmišljanja.
[ galet@world @ 10.05.2009. 19:30 ] @
Ne može se nešto stvoriti niti postojeće uništiti. Klepetanja o knjigama i u knjigama koje ovo
poriču mogu uvažavati samo oni koji ne razmišljaju nego veruju u nemoguće.
[ Cabo @ 10.05.2009. 19:34 ] @
Hm, izgleda da imam grešku u rezonovanju, jer sam pisao u brzini. Prvo,  nije neutral za sabiranje, već upravo suprotno, svi konačni brojevi su neutrali za sabiranje za  . Drugo,  nije jedinstven po ovoj definiciji, jer  , pa ne mora da bude kontradikcija 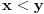 (  može da bude beskonačnost „višeg reda“ u odnosu na  ). Pre bi se „broj“  mogao shvatiti kao klasa ekvivalencije, nešto što se slično ponaša kao operacija „malo o“, 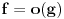 . A 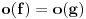 ne mora da znači da je 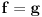 , već samo da te dve funkcije pripadaju istoj klasi ekvivalencije.
Imajući to u vidu, da,  se formalno predstavlja ili nizovima ili funkcijama, a Hajne (ako se ne varam) je dokazao da je limes niza ekvivalentan limesu funkcije.
U suštini, u Analizi 1 se i ne proučava „broj  “, već ili „beskonačan interval“ ili „beskonačan limes“.
Prva godina MATF-a, ej!  Da me vidi neki profan sada...  [ Cabo @ 10.05.2009. 19:45 ] @
Citat: galet@world: Ne može se nešto stvoriti niti postojeće uništiti. Klepetanja o knjigama i u knjigama koje ovo
poriču mogu uvažavati samo oni koji ne razmišljaju nego veruju u nemoguće.
Priroda je konačna, beskonačnost je apstraktan pojam (pa su neki filozofirali da su konačni brojevi ljudski, a da je beskonačnost „božanska“). Matematika je apstraktna nauka koja barata sa apstraktnim, zamišljenim, objektima. Nije to biologija pa da se kaže: evo deco, ovo je šargarepa a tamo možete da vidite žabu.
U suštini, ni tvojih 100 kg pšenice nije baš tačno 100 kg, jer se samo može izmeriti sa ograničenom tačnošću. E, time se bavi numerička matematika.
Šta ti misliš, da si pametniji od svih matematičara od Euklida pa naovamo? Svi oni greše, samo si ti u pravu? Da, naravno. [ holononi @ 10.05.2009. 22:06 ] @
Trebao si definisati a + ∞ = ∞ + a = ∞ i a·∞ = ∞·a = ∞ za a < ∞ i 0·∞ = 0. Za ovako datu definiciju važe komutativnost, asocijtivnost i distributivnost na skupu [0,∞]. Onda si mogao preći na dokazivanje. Medjutim pošto sam iz konteksta pretpostavio da misliš na ovo nema potrebe. Uz napomenu da je RU{∞} kompaktan topološki prostor a R nije.
Eh moj mali epsilone, gde je tvoja draga delta ?
[ galet@world @ 11.05.2009. 08:08 ] @
Po mojoj računici vrednost ove funkcije 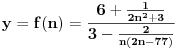
je veća od 2 čak i ako kažemo da je n = ∞, ali se ne može reći za koliko je veća. [ holononi @ 11.05.2009. 09:18 ] @
je nepostojanje pa je takav stav netačan. Dokaz
Citat: Ne može se nešto stvoriti niti postojeće uništiti. Klepetanja o knjigama i u knjigama koje ovo
poriču mogu uvažavati samo oni koji ne razmišljaju nego veruju u nemoguće.
jer je
postojanje. QED
[ Nedeljko @ 11.05.2009. 11:04 ] @
Citat: galet@world: Ne može se nešto stvoriti niti postojeće uništiti. Klepetanja o knjigama i u knjigama koje ovo
poriču mogu uvažavati samo oni koji ne razmišljaju nego veruju u nemoguće.
Tebi je definitivno mesto na forumu za magiju, alhemiju i slične discipline. U matematici se vrdo dobro zna šta je realan broj. šta limes, šta beskonačna suma, šta prebrojiv, a šta neprebrojiv skup itd. [ Nedeljko @ 11.05.2009. 13:43 ] @
Je li Galet, ko je ovde osim tebe pominjao "stvaranje i uništavanje ex nihilis" i sličnu tematiku?
[ galet@world @ 11.05.2009. 15:24 ] @
Egzinstencijalna nula je rezultat deljenja, a apsolutna nula je rezultat oduzimanja.
Prethodne primedbe ne stoje jer su rezultat nepoimanja ovih pojmova i nerazumevanja razlike među njma.
Citat: Nedeljko: Je li Galet, ko je ovde osim tebe pominjao "stvaranje i uništavanje ex nihilis" i sličnu tematiku?
Potraži - svi su postovi tu! [ Cabo @ 11.05.2009. 17:13 ] @
Citat: galet@world: Egzinstencijalna nula je rezultat deljenja, a apsolutna nula je rezultat oduzimanja.
Prethodne primedbe ne stoje jer su rezultat nepoimanja ovih pojmova i nerazumevanja razlike među njma.
Potraži - svi su postovi tu!
Kada odgovoriš na pitanje da li možeš da napišeš beskonačan broj jedinica, odgovoriću kako je moguće „uništiti“ 100 kg pšenice. [ Nedeljko @ 11.05.2009. 17:14 ] @
Zanimljivo je videti kako neko komentariše nešto u šta nije upućen. Hteo bi umesto strogo i korektno ivedenih realnih brojeva, limesa i teorije mere da nam prodaš neku praznu priču u kojoj osim magle nigde nema konkretnog modela.
[ Cabo @ 11.05.2009. 17:30 ] @
A i ovo:
Citat: galet@world: Po mojoj računici vrednost ove funkcije 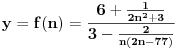
je veća od 2 čak i ako kažemo da je n = ∞, ali se ne može reći za koliko je veća.
Niko tu ne kaže da je  , već 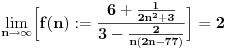 ( primeti limes, 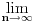 ! !), a to po definiciji znači da je 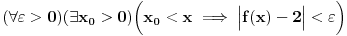 .
To znači, rečima: ma koliko da izabereš mali broj, recimo: 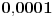 ili čak 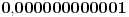 itd., ja ću uvek naći toliko veliki broj  da će za sve  koji su strogo veći od tog mog broja razlika između vrednosti funkcije od tog mog broja i broja 2 biti manja od tvog broja.
Može se, dalje, oceniti u koju klasu ekvivalencije beskonačno malih funkcija spada taj „ostatak“ koji „fali“ do dvojke u zavisnosti od „mog broja“. U ovom konkretnom slučaju, recimo, radi se o 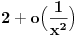 kad 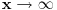 . Kaže se i: kojom brzinom funkcija  konvergira ka dvojci.
[Ovu poruku je menjao Cabo dana 11.05.2009. u 18:50 GMT+1][ igorpet @ 11.05.2009. 17:51 ] @
Citat: Ja tvrdim da je 0 + 0 + 0 = 3•0
Pratim temu od pocetka, ali nisam bas uspeo da shvatim oko cega se sporite!!!
Jel se sporite oko CRVA? 
Teorema:
Dva puta nista jednako nista, cista matematika.
Sinko, crva nije ni bilo!
Dokaz (vizuelni):   http://www.netbioskop.com/crta...onije-crv-video_82cef5482.html
http://www.netbioskop.com/crta...onije-crv-video_82cef5482.html
narocitu paznju obratiti od 5:37
Ako jos nesto nije jasno obratite se Sofroniju  [ Nedeljko @ 11.05.2009. 18:09 ] @
[ Nedeljko @ 11.05.2009. 18:30 ] @
@Cabo,
Da je njega zanimalo to o čemu pišeš, odavno bi to negde pročitao. Dobijao je i linkove, ali džaba, tera svoje, pa tera. Bitno je "da je on u pravu, ali da cela matematika ne valja", mada je ne poznaje i ne želi da je nauči (jer kako bi onda bio "u pravu"). Ali zato, prosipa i drvlje i kamenje.
[ Cabo @ 11.05.2009. 18:42 ] @
Citat: Nedeljko: @Cabo,
Da je njega zanimalo to o čemu pišeš, odavno bi to negde pročitao. Dobijao je i linkove, ali džaba, tera svoje, pa tera. Bitno je "da je on u pravu, ali da cela matematika ne valja", mada je ne poznaje i ne želi da je nauči (jer kako bi onda bio "u pravu"). Ali zato, prosipa i drvlje i kamenje.
Zato sam rekao da je tema zrela za zaključavanje, i to nije nikakvo „skrivanje“ mene i ostalih. Stvari treba nazvati pravim imenom. Galet očito neće da vodi dijalog, već monolog. [ galet@world @ 11.05.2009. 18:44 ] @
Citat: Nedeljko: Zanimljivo je videti kako neko komentariše nešto u šta nije upućen. Hteo bi umesto strogo i korektno ivedenih realnih brojeva, limesa i teorije mere da nam prodaš neku praznu priču u kojoj osim magle nigde nema konkretnog modela.
Ima, ima samo treba videti, ali kad ljudima zbog sujete padne mrak (magla) na oči onda ništa ne vide - jedino da pokušam, kad već ne vide,
da im pružim model koji se može napipati. [ Fitopatolog @ 11.05.2009. 18:57 ] @
Dane - Dane... MATEMATIČARE jedan...!!!
[ Nedeljko @ 11.05.2009. 19:22 ] @
Citat: galet@world: Ima, ima samo treba videti, ali kad ljudima zbog sujete padne mrak (magla) na oči onda ništa ne vide - jedino da pokušam, kad već ne vide, da im pružim model koji se može napipati.
Ne znam Galet, kompletno uređeno polje ima vrlo konkretan i precizno definisan model. Uvedeš relaciju ekvivalencije između Košijevih nizova racionalnih brojeva kao "razlika im teži nuli", pa su realni brojevi odgovarajuće klase ekvivalencije, pa se lepo uvedu operacije nad tim klasama itd.
Kod tebe nigde nema ni aksioma ni modela. Kao i na temi o teoriji relativnosti, očekuješ da ti neko drugi formuliše tvoje ideje (ono sa "stvarnom brzinom tela nezavisnom od koordinatnog sistema"). [ galet@world @ 11.05.2009. 20:07 ] @
Ma možete vi da pričate šta hoćete, ali pojam egzistencijalne nule je tu i ne može se odbaciti, a i opis
koji sam dao o jednoj i drugoj nuli nesumnjivo pokazuje razliku među njima. Nisam dao preciznu definiciju,
ali me ne možete ubediti da niste razumeli šta je jedna a šta druga nula. Zašto da ja dajem preciznu
definiciju kad verujem da ćete vi, ako sam uspeo da kažem šta mislim i ako ste me razumeli, to bolje
učiniti.
[ Cabo @ 11.05.2009. 20:26 ] @
Citat: galet@world: Ma možete vi da pričate šta hoćete, ali pojam egzistencijalne nule je tu i ne može se odbaciti, a i opis
koji sam dao o jednoj i drugoj nuli nesumnjivo pokazuje razliku među njima. Nisam dao preciznu definiciju,
ali me ne možete ubediti da niste razumeli šta je jedna a šta druga nula. Zašto da ja dajem preciznu
definiciju kad verujem da ćete vi, ako sam uspeo da kažem šta mislim i ako ste me razumeli, to bolje
učiniti.
Čekaj da vidim da li sam dobro razumeo: hoćeš da polemišeš, ali da mi pišemo i tvoj i naš tekst? o_O
Duhovit si, nema šta.
Da si dovoljno matematički obrazovan da formalno formulišeš svoje stavove, ne bi ih imao. [ galet@world @ 12.05.2009. 07:29 ] @
Citat: Cabo: Da si dovoljno matematički obrazovan da formalno formulišeš svoje stavove, ne bi ih imao.
Imao bih, ali sigurno ne poput tvojih. [ Nedeljko @ 12.05.2009. 07:38 ] @
Citat: Cabo: Čekaj da vidim da li sam dobro razumeo: hoćeš da polemišeš, ali da mi pišemo i tvoj i naš tekst? o_O
Duhovit si, nema šta.
Kao i na temi o teoriji relativnosti, gde je od mene očekivao da mu definišem njegov pojam "stvarne brzine tela" (nezavisan od koordinatnog sistema), kome sam se protivio.
Ne, Galet, svoje stavove moraš sam da braniš. Zasnivanje realnih brojeva i teorije mere je tu, bez obzira da li ti želiš to da čitaš ili ne. Ne možeš ga oboriti, pogotovu ne metodom neznanja. Možeš da pokušaš da ponudiš neko drugo zasnivanje, ali to je onda tvoj posao. [ Cabo @ 12.05.2009. 16:48 ] @
Citat: galet@world: Imao bih, ali sigurno ne poput tvojih.
Ne, i dalje sam ubeđen da tvoji stavovi počivaju isključivo na odbijanju da upoznaš matematiku. Imao sam i ja svakakve stavove dok sam bio brucoš, ali se vremenom sve to izbrusi.
Jedan od osnovnih preduslova da neko postigne uspeh u shvatanju matematike jeste spremnost na priznavanje sopstvenih grešaka i kritički odnos prema sopstvenim stavovima. Ja smatram da posedujem te osobine. Vremenom neke stvari zaboravim, ali su zato tu drugi učesnici koji me isprave, kao i ja njih po potrebi. Sem toga, još čuvam sve udžbenike i sveske, pa sam se tako, na primer, lako podsetio definicije limesa u mojih nekoliko poslednjih poruka u ovoj temi, iako sam Analizu 1 davno položio. [ galet@world @ 12.05.2009. 19:29 ] @
Citat: Nedeljko: Kao i na temi o teoriji relativnosti, ...
Bolje bi bilo da tu temu zaboraviš - tamo si mnnogo više grešio - stalno sam morao da te korigujem.
[ Nedeljko @ 12.05.2009. 19:33 ] @
Moraću da te razočaram - sve je dokumentovano i sve se lepo vidi.
[ Kolins Balaban @ 12.05.2009. 22:28 ] @
nekad mi drago sto nisam matematicar, pogotovo teoreticar. umjesto da se ovdje svadjate i ponavljate jedno te isto, i ono sto je u mnogim knjigama napisano, korisnije bi bilo da ste nekoj babi otisli i oprali tepihe :P:P :) hehehe iskreno, od ovog NEMA HAJRA NI KORISTI COVJECANSTVU! ne mogu shvatiti ljude, koji su godine svog zivota proveli na dokazivanju npr. posljednje Ferma-ove teoreme. bolje da su grobove kopali djabe, makar bi nekom pomogli (snizili cijenu sahrane koja danas nije mala).
[ galet@world @ 13.05.2009. 06:27 ] @
Citat: Nedeljko: Moraću da te razočaram - ...
To si odavno počeo da činiš - izuzev ponekog prećutnog priznanja grešaka -("sve se lepo vidi") [ Nedeljko @ 13.05.2009. 10:35 ] @
Citat: galet@world: To si odavno počeo da činiš - izuzev ponekog prećutnog priznanja grešaka -("sve se lepo vidi")
Isti autor, iste metode. Pre toga si u nemogućnosti da sam dokažeš svoje stavove očekivao od protivnika tih stavova da ih oni dokazuju, a sad meni imputiraš šta sam hteo da kažem. Što se grešaka tiče, samo prepusti posetiocima da procenjuju ko je lupao i koliko.
Citat: Kolins Balaban: nekad mi drago sto nisam matematicar, pogotovo teoreticar. umjesto da se ovdje svadjate i ponavljate jedno te isto, i ono sto je u mnogim knjigama napisano, korisnije bi bilo da ste nekoj babi otisli i oprali tepihe :P:P :) hehehe iskreno, od ovog NEMA HAJRA NI KORISTI COVJECANSTVU! ne mogu shvatiti ljude, koji su godine svog zivota proveli na dokazivanju npr. posljednje Ferma-ove teoreme. bolje da su grobove kopali djabe, makar bi nekom pomogli (snizili cijenu sahrane koja danas nije mala).
Od ove teme nema nikakve koristi čovečanstvu. Sa tim se slažem, ali tvrditi tako nešto za veliku Fermaovu teoremu... Reklo bi se da smo razvojem nauke dobili mnogo štošta što nismo imali, a da je ono što smo imali itekako pojeftinilo. [ galet@world @ 13.05.2009. 14:55 ] @
Citat: Nedeljko:Što se grešaka tiče, samo prepusti posetiocima da procenjuju ko je lupao i koliko.
To je već prepušteno posetiocima. Možda se uzdaš se u princip većine iliti izglasavanja, ali uzalud. To ne podleže tom principu. [ Nedeljko @ 13.05.2009. 17:22 ] @
Mora da podleže tvojim principima - što ti kažeš, to je tako i drugi ima da misle ono što im ti imputiraš kao meni danas.
Citat: galet@world: To si odavno počeo da činiš - izuzev ponekog prećutnog priznanja grešaka -("sve se lepo vidi")
Samo ti pusti posetioce i njihove principe, jer si inače čuven po svojim principima:
1. Izneseš neki stav sa kojim se drugi ne slažu, pa u nemogućnosti da ga dokažeš, pozivaš protivnike tog stava da ga dokažu, pa ako ga ne dokažu, onda nemaju pojma.
2. Kritikuješ stavove koje ne razumeš i ne pokušavaš da saznaš kontekst u kojem su formulisani, već im lepiš svoje interpretacije i tako ih "obaraš".
Da se popravim, princip 2 nije tvoj i ima ime - vađenje iz konteksta, ali princip 1 je verovatno originalno tvoj. Za njega ti svaka čast. [ Cabo @ 13.05.2009. 17:32 ] @
Ponavljam apel za zaključavanje teme.
-- ZAKLjUČ --
I rešen problem. Ako se trolovanje nastavi - ban.
[ igorpet @ 13.05.2009. 18:43 ] @
Citat: Cabo: Ponavljam apel za zaključavanje teme.
-- ZAKLjUČ --
I rešen problem. Ako se trolovanje nastavi - ban.
Tema se jeste malo rasplinula, i krenula sa blagim licnim "peckanjima", ali neka je bre ... (sve dok je u okviru domaceg vaspitanja).
I ja ne kapiram bas sta Galet zeli da dokaze, i nacin na koji to radi ali OK ...
Nekad su neke koji su razmisljali drugacije spaljivali na lomaci, ali valjda smo malo evoluirali od tada ... [ galet@world @ 13.05.2009. 18:48 ] @
Citat: Nedeljko:
1. Izneseš neki stav sa kojim se drugi ne slažu, pa u nemogućnosti da ga dokažeš, pozivaš protivnike tog stava da ga dokažu, pa ako ga ne dokažu, onda nemaju pojma.
Na primeru sa graničnim tetivama stav je i pokazan i dokazan u suštini - stroga verbalna definicija je nužna,
ali njen izostanak je formalne prirode i ne eliminiše istinitost tog stava. Kao i obično - nisi dokazao suprotno.
Citat: 2. Kritikuješ stavove koje ne razumeš i ne pokušavaš da saznaš kontekst u kojem su formulisani...
Kontekst u kom je formulisana glupost: a/∞ = a - a zaista ne razumem niti pokušavam jer to mogu samo
moderni relativistički vernici i njima slični. Istina ne zavisi od konteksta. [ Nedeljko @ 13.05.2009. 19:39 ] @
Citat: galet@world: Na primeru sa graničnim tetivama stav je i pokazan i dokazan u suštini - stroga verbalna definicija je nužna, ali njen izostanak je formalne prirode i ne eliminiše istinitost tog stava. Kao i obično - nisi dokazao suprotno.
"Dokazao si" tako što si jednostavno ignorisao protivargumente koji su ti predočeni. A to što zoveš formalnom prirodom je esencijalnog karaktera. To je kao da neko tvrdi da je ažbakar bele boje, a da se ne zna šta je ažbakar.
Šta tebi vredi dokazivati bilo šta, kad samo teraš monolog i ne interesuje te šta druga strana piše.
Citat: galet@world: Kontekst u kom je formulisana glupost: a/∞ = a - a zaista ne razumem niti pokušavam jer to mogu samo
moderni relativistički vernici i njima slični. Istina ne zavisi od konteksta.
Ne znaš šta znači neki iskaz, ali znaš da je glupost! Zanimljivo. A ovo sa nezavisnošću istine od konteksta je čuveni "biser" (nisi ga ti izmislio). [ Nedeljko @ 14.05.2009. 13:45 ] @
Predlažem prelazak na temu o teoriji relativnosti.
http://www.elitesecurity.org/p2219871
Nije ništa manje zanimljivo nego ovde. [ galet@world @ 14.05.2009. 22:58 ] @
Citat: Nedeljko:
"Dokazao si" tako što si jednostavno ignorisao protivargumente koji su ti predočeni.
Evo „protivargumenata“
- prava je kružnica s beskonačnim radijusom –
koliko centara ima ova prava, koliko zajedničkih tačaka ima sa tangentom, što prava ne bi bila sinusoida sa nultom amplitudom
y = rsinx gde je r = 0 i slične proizvoljne izmišljotine.
- interval je skup tačaka –
interval ima dimenziju – tačka nema, interval je poseban entitet i može se objašnjavati samo samim sobom, a ne nečim što
on nije
- e ovo je sad zavrzlama –
u ovom postu autoru se omaklo pa je rekao – tu je dužina nula – ali nije rekao – tu nema dužine
- nerazlikovanje postojanja pozajmice od vrednosti pozajmice –
i ovo je jedan od „kontraargumenata“
- nisam tvrdio da je 0 + 0 = 0 glupost ako je nula apsolutna –
izmišljate nešto što nisam rekao pa tu izmišljotinu kritikujete
- pojam granične tetive nije definisan –
kako ovo može biti kontraargument?
- tetiva prelazi u tačku –
tetiva ne prelazi ni u šta – ona nestaje
- sin x/sin x nije definisano ako je x = 0 –
tendenciozno podmetanje nedefinisanog deljenja sa nulom tamo gde to nije slučaj
- "dokaz" –
Šta se dokazuje pisanjem oduzimanja na drugi način t. j. kao sabiranje sa negativnim brojevima
uz upotrebu izraza 1/ ∞ = 0 za koji tvrdiš čas da je 0 čas da nije 0:
„Što se pšenice tiče, zavisi kakva je raspodela pčenice u prostoru i kako se vrši delenje. Primera radi, ja mogu da izdvojim polovinu pšenice kao prvi deo. Drugi deo će mi biti polovina od preostale polovine. Treći deo će mi biti polovina od preostale četvrtine i tako dalje. n-ti deo će imati masu 100kg/2n. I to je jedan od načina delenja pšenice na beskonačno mnogo delova, ali kod njega svaki deo ima veću masu od nule.“
Ne bi se trebalo brukati tvrdeći čas jedno čas drugo nalazeći spas „u kontekstu“.
- beskonačnost „jede realne brojeve“ – i t. d. i t. d.
Posle ovakvih "kontraargumenata" ne treba se čuditi monologu.
Citat: Ne znaš šta znači neki iskaz, ali znaš da je glupost! Zanimljivo.
Znam šta znači i znam da ga tumačiš uglavnom pogrešno, ako ti se slučajno ne omakne da ga ponekad i
ispravno protumačiš
Citat: A ovo sa nezavisnošću istine od konteksta je čuveni "biser" (nisi ga ti izmislio).
Opet relativistička opsednutost.
Citat: Nedeljko: Predlažem prelazak na temu o teoriji relativnosti.
Čemu? Već znam šta znaš. Tamo je još veći izbor "kontraargumenata" [ axx420 @ 15.05.2009. 00:28 ] @
Citat: galet@world: Nadam se, pošto je ovo forum za matematiku, da i nematematičari mogu postaviti poneko principijelno pitanje.
Evo šta mene muči:
Ako kružnicu posmatramo iznutra onda je ona konkavna, a ako je posmatramo spolja ona je konveksna što bi
trebalo da znači da je konveksna strana duža od konkavne.
Ako pak smatramo da su obe strane jednako dugačke onda bi dobili pravu jer to je svojstvo prave.
Ako je odgovor da kružnica nema dve strane nego da je to uvek samo jedna strana - odakle onda potiče
zakrivljenost i kako se ona objašnjava kod bilo kakve krive?
Ovo verovatno ne spada u ovu temu pa ako moderator smatra da je interesantno neka ovom nađe neko drugo
mesto.
Za neku proizvoljnu kružnicu sa poluprečnikom r važi:
- Dužina kružnice "iznutra" je 2rPI
- Dužina kružnice "spolja" je 2rPI
Sasvim je svejedno šta je konkavno a šta konveksno, dužina kružnice je ista "iznutra" i "spolja" jer je rastojanje od centra kružnice isto: r.
Citat: galet@world: Pade mi napamet sledeći "eksperiment":
Ako iz ravni po nekoj kružnici isečemo i izvadimo krug šta dobijamo:
1. rupu ograničenu kružnicom
2. krug ograničen kružnicom
Dakle imamo dve kružnice. Kako da vratimo krug u ravan?
1. Ako su kružnice jednake onda se tačke kružnica poklapaju, zar ne?
2. Ako se tačke kružnica ne poklapaju onda kružnice nisu jednake.
Tačke kružnica se ne poklapaju jer je presecajuća kružnica bila između njih.
Ovo mi liči na paradoks koji je možda već neko pre mene postavio.
Na kojoj udaljenosti od centra kružnice su:
1. rupa ograničena kružnicom
2. krug ograničen kružnicom
3. "ono između njih"
"Ako te već zanima koliko konj ima zuba što jednostavno ne otvoriš konju usta i prebrojiš ih?"
Pozdrav svima i svako dobro. [ galet@world @ 15.05.2009. 09:30 ] @
Citat: axx420: "Ako te već zanima koliko konj ima zuba što jednostavno ne otvoriš konju usta i prebrojiš ih?"
Mogao bih da ti odgovorim u istom stilu i jednom jedinom rečju, ali to bi bila šala koja ovde nije dozvoljena.
Citat: Pozdrav svima i svako dobro.
Živ bio i veselio se! Ako si pogodio koja je to reč - nemoj da se ljutiš. Šala je šala [ Nedeljko @ 15.05.2009. 11:14 ] @
Zaboravio si na protivargumente kao
Citat: Nedeljko: I šta je na kraju definicija granične tetive? Nemoj samo da mi pominješ "poslednji trenutak pre..." jer takav trenutak ne postoji - između svaka dva trenutka postoji beskonačno mnogo trenutaka.
Ako ti to nije jasno, probaj da iz  izvedeš  .
Citat: galet@world: - interval je skup tačaka –
interval ima dimenziju – tačka nema, interval je poseban entitet i može se objašnjavati samo samim sobom, a ne nečim što on nije
Interval jeste skup tačaka. To ne znači da se pojam intervača "objašnjava" pojmom tačke, već da je definisan preko njega, kao što krug možeš definisati preko pojmova tačke, ravni i podudarnosti parova tačaka. Ne znam odakle ti ideja da zbog toga krug mora imati zajedničke osobine sa tim pojmovima. Da, ima sličnosti sa skupovima tačaka - jer je uži pojam od tog.
Što se nule tiče, ona nije ništa, već je nešto - element skupa realnih brojeva. Skup {0} ima jedan element (nulu), a ne nijedan (nije prazan skup).
{to se mere tiče, mera intervala kao skupa tačaka jednaka je širini tog intervala, a mera tačke (ili preciznije jednočlanog skupa koji sadrži samo jednu tačku) je nula. Da bi iz toga izveo protivrečnost, treba ti stav da ako je 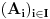 familija merljivih disjunktnih skupova da je onda 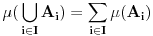 . Međutim, taj stav bi morao da dokažeš - u teoriji mere ga nema (tj. ima samo za najviše prebrojive familije, a interval je neprebrojiv skup tačaka).
Citat: galet@world: - pojam granične tetive nije definisan –
kako ovo može biti kontraargument?
A kako se možeš pozivati na pojam čije značenje nije definisano?
Citat: galet@world: - "dokaz" –
Šta se dokazuje pisanjem oduzimanja na drugi način t. j. kao sabiranje sa negativnim brojevima
uz upotrebu izraza 1/ ∞ = 0 za koji tvrdiš čas da je 0 čas da nije 0:
„Što se pšenice tiče, zavisi kakva je raspodela pčenice u prostoru i kako se vrši delenje. Primera radi, ja mogu da izdvojim polovinu pšenice kao prvi deo. Drugi deo će mi biti polovina od preostale polovine. Treći deo će mi biti polovina od preostale četvrtine i tako dalje. n-ti deo će imati masu 100kg/2n. I to je jedan od načina delenja pšenice na beskonačno mnogo delova, ali kod njega svaki deo ima veću masu od nule.“
A kada sam tvrdio da  nije nula? To što pokušavaš da sipaš pšenicu u formulu je plod tvoje bolesne mašte. Na pšenični argument sam odgovorio, ali nisam dobio nikakav odgovor. Da, ja mogu interval širine 1 pdeliti na beskonačno mnogo intervala od kojih nijedan nema dužinu nula, kao što ga mogu podeliti i na dva dela, a da nijedan nema dužinu 1/2. U čemu je problem?
[ miki069 @ 15.05.2009. 12:48 ] @
CITAT:
"Evo šta mene muči:
Ako kružnicu posmatramo iznutra onda je ona konkavna, a ako je posmatramo spolja ona je konveksna što bi
trebalo da znači da je konveksna strana duža od konkavne.
Ako pak smatramo da su obe strane jednako dugačke onda bi dobili pravu jer to je svojstvo prave."
- Smatramo da su obe strane jednako dugačke O = 2*r*pi.
- Iz toga se ne može zaključiti da je kružnica isto što i prava.
"broj 15 ima svojstvo da je deljiv sa 3 onda zaključujemo da je on jednak broju 21 jer je to je svojstvo broja 21."
Ako ti je jasno šta mene "muči" u ovom "dokazu" da je 15=21 onda si rešio šta tebe muči u dokazu kružnica = prava.
"Zaboravljam" da broj 21 ima i svojstvo da je deljiv sa 7 a broj 15 ga nema.
Imao sam samo potreban ali ne i dovoljan uslov.
[ galet@world @ 15.05.2009. 14:05 ] @
Citat: Nedeljko: Da, ja mogu interval širine 1 pdeliti na beskonačno mnogo intervala od kojih nijedan nema dužinu nula, kao što ga mogu podeliti i na dva dela, a da nijedan nema dužinu 1/2. U čemu je problem?
U tome što si rekao da je 1/ ∞ = 0,
U tome što smatraš da je interval koji ima dimenziju skup tačaka koje nemaju dimenziju
što je jednako tvrdnji da se iz ničega može dobiti nešto, a to je plod tvog bolesnog razuma.
Sad će gospoda koja te štite da opomenu mene jer sam ti odgovorio istom merom, a ne tebe
koji uvek prvi startuješ sa bezobrazlukom. [ Nedeljko @ 15.05.2009. 14:17 ] @
Citat: galet@world: Znam šta znači i znam da ga tumačiš uglavnom pogrešno, ako ti se slučajno ne omakne da ga ponekad i ispravno protumačiš
I šta znači iskaz  ? Prosvetli me!
A što se tiče "nezavisnosti istine od konteksta", taj princip se primenjuje samo na tebe - ti možeš da nalupavaš kontekste kako hoćeš. Sa druge se primenjuje sasvim drugi princip po kome tuđa tumačenja kvalifikuješ kao pogrešna i ispravna. [ Nedeljko @ 15.05.2009. 14:25 ] @
Kakve to veze ima jedno sa drugim? Dakle, podelimo interval širine 1 na jedan interval širine 1/2, još jedan širine 1/4, još jedan širine 1/8 itd. i odatle sledi da je 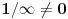 . Ili, podelimo interval širine 1 na jedan interval širine 1/3 i jedan interval širine 2/3 i odatle sledi da je 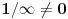 . O čemu ti to leba ti?
Citat: galet@world: U tome što smatraš da je interval koji ima dimenziju skup tačaka koje nemaju dimenziju što je jednako tvrdnji da se iz ničega može dobiti nešto, a to je plod tvog bolesnog razuma.
Stvaranje, uništavanje i ostale nematematičke kategorije samo ti ovde pominješ i to je tvoj lični problem. Rekoh ja da ti je mesto očigledno na forumu za alhemiju, magiju i slične discipline. Takođe, tačka nije ništa, već nešto.
Što se tiče izraza "plod bolesne mašte" i sličnih, možeš slobodno da ga koristiš koliko hoćeš.
[ Cabo @ 15.05.2009. 15:50 ] @
[ Bojan Basic @ 15.05.2009. 16:03 ] @
Citat: Cabo:
Zato sam rekao da je tema zrela za zaključavanje, i to nije nikakvo „skrivanje“ mene i ostalih. Stvari treba nazvati pravim imenom. Galet očito neće da vodi dijalog, već monolog.
U poslednjoj rečenici leži suština onoga što me je odvraćalo od zaključavanja ove teme. Nije tačno da galet@world vodi monolog, upravo suprotno — s njim nadugačko i naširoko komunicira broj učesnika koji je znatno iznad proseka diskutanata po temi u ovom forumu. Ukoliko i svi oni imaju nešto da kažu, ispada da ne bi bilo u redu zaključati je tek tako.
Jasno je da njegove ideje, iako možda imaju smisla uz neke druge postulate (kao što su postulat o nepismenoj babi i postulat o pšenici), ne odgovaraju važećim matematičkim aksiomima, i samim tim nisu iznete na pravom mestu — i sam naziv ovog foruma, Matematika, kazuje da se ovde govori o matematici kakva jeste, a ne o nekoj kakva bi mogla biti ukoliko bi se usvojile ispravke ili „ispravke“ koje galet@world predlaže. Ujedno se usuđujem reći da niko od članova ovog foruma nema dovoljno matematičkoj uticaja da za njegovo ideje lobira bilo na kom relevantnom mestu (u pokušaju da se one usvoje, tj. da se postojeće zasnivanje skupa realnih brojeva eventualno izmeni/dopuni), pa je zato bolje, što i predlažem, da galet@world pokuša s obraćanjem nekome od vodećih svetskih matematičara, ko bi možda i mogao da napravi nešto od toga (ukoliko proceni da to ima smisla).
Razlog zašto se konačno javljam jeste to što je diskusija prešla sa teorijskog nivoa (kakav god on bio) na lični, tj. na pominjanje „bolesnog razuma“ (što s jedne, što s druge strane). Svako, naravno, ima pravo na svoje mišljenje i bez diplome neuropsihijatra, ali to što na ES-u ne postoji forum za medicinu (mada verujem da bi se i tamo dozvoljavali samo stručniji nalazi) ne znači da medicinske teme prebacujemo na matematički kutak. Galet@world bi eventualno mogao prihvatiti da, ukoliko već teoriju na koju mu ostali članovi skreću pažnju smatra produktom bolesnog razuma, to svakako nije Nedeljkov razum, već razum nekih čika koje su to smislile, a što Nedeljko i ostali samo prenose — te ga tom prilikom upućujem da još jednom pročita prethodni pasus (onaj o pravoj adresi za obraćanje).
Temu bih završio citatom Farenhajtove poruke:
Citat: Farenhajt:
Pa, do đavola, okačite neki zanimljiv i dobar problem koji ste našli u literaturi, sreli u praksi ili pak sami smislili, ili uzmite pa rešite neki od objavljenih zadataka. To će mnogo više doprineti svačijem matematičkom čulu i znanju nego insistiranje na apsolutno somnambulnim diskusijama,
uz predlog da počnete odavde.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|