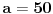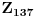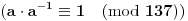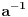[ plotter @ 26.04.2009. 14:10 ] @
|
[ Bojan Basic @ 26.04.2009. 15:17 ] @
U rešenju je greška.
[ plotter @ 26.04.2009. 15:50 ] @
OK. Da li neko moze da napise kako "na papiru" doci do tacnog resenja za ovaj primer, kompajler ne smem da nosim na ispit :)?
Deo sa pronalazenjem GCD mi je jasan, posle je potrebno odraditi neki reverzan proces, ali taj deo nije bas najbolje objasnjen. [ Cabo @ 04.05.2009. 22:08 ] @
Citat: plotter: OK. Da li neko moze da napise kako "na papiru" doci do tacnog resenja za ovaj primer, kompajler ne smem da nosim na ispit :)? Deo sa pronalazenjem GCD mi je jasan, posle je potrebno odraditi neki reverzan proces, ali taj deo nije bas najbolje objasnjen. 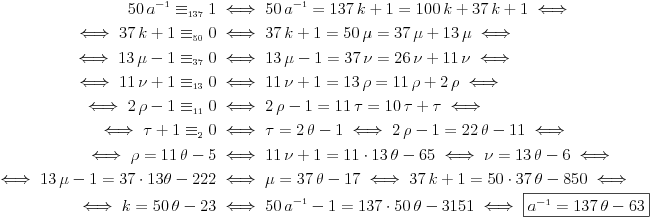 Dakle, sva celobrojna rešenja su oblika 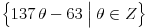 , pa se za, recimo, , pa se za, recimo, 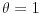 lako dobija lako dobija 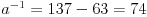 . Inače, i . Inače, i 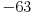 se smatra inverzom od se smatra inverzom od 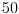 , jer je , jer je 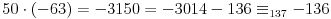 , pa je , pa je  za za 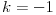 , i na kraju , i na kraju 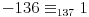 . .[Ovu poruku je menjao Cabo dana 04.05.2009. u 23:24 GMT+1] [ plotter @ 31.05.2009. 15:05 ] @
Malo kasnim sa odgovorom ali ne zameri, hvala, ovo je bilo od velike pomoci.
Pozdrav [ Cabo @ 31.05.2009. 21:25 ] @
Nema problema, zašto bih zamerio?
I ja sam razbijao glavu sa ovim dok nisam provalio. Niko od profesora i asistenata nije hteo (ili nije umeo) da mi ovo lepo, natenane, objasni. Kao što rekoh, sindrom „ispod časti“ na delu. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|