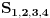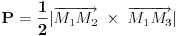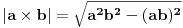Kako su površi tetraedra trouglovi, može se izračunati površina stranica po obrazcu za izračunavanje površine trougla datom vektorom položaja temena u prostoru



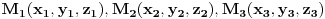a površina se računa po obrascu: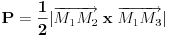



Iste te tačke temena tetraedra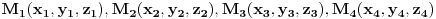



se koriste za izračunavanje zapremine tatraedra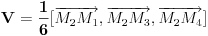



Ostalo je da se vidi kako to iskombinovati.

Misliš

[tex]P=\frac{1}{2}|\overrightarrow{M_{1}M_{2}} \; \times \; \overrightarrow{M_{1}M_{3}}|[/tex]

?

Upravo tako, vektorski proizvod, pa intenzitet pa pola od toga.

U vektorskoj algebri važi identitet .

Obzirom da je desna strana planarnog karaktera, podesna je za računanje površine trougla u prostoru bilo koje dimenzije. Uopštenje ovoga je Gramova determinanta.

Još samo ostaje da se uspostavi bijekcija izmedju zapremine tetraedra i površine njegovih strana. Treba neko da bude vredan pa da bar probije led. Posle će se to pojaviti kao zadatak na nekom pismenom.

Evo nečeg vrlo sličnog, gde ne figuriraju površine strana, nego dužine ivica.

Šta mu je tu "right tetrahedrons", da li je to isto što "regular tetrahedrons"?