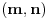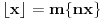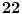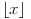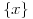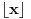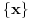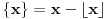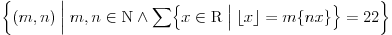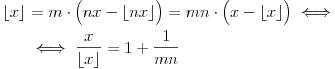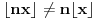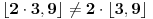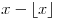[ Farenhajt @ 30.04.2009. 16:08 ] @
|
[ Cabo @ 04.05.2009. 20:44 ] @
[ Bojan Basic @ 04.05.2009. 21:37 ] @
[ Cabo @ 05.05.2009. 15:38 ] @
[ Farenhajt @ 05.05.2009. 17:06 ] @
[ Cabo @ 07.05.2009. 17:15 ] @
[ Farenhajt @ 09.05.2009. 23:48 ] @
Pošto ni ovde, izgleda, nema interesenata, okačiću svoje rešenje.
Stavimo 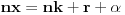 , gde je , gde je 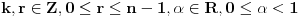 . .Tada je 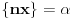 i i 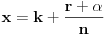 , ali pošto je , ali pošto je 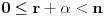 , dobijamo , dobijamo 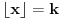 Stoga je, po početnoj jednačini, 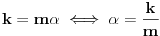 . Prema definiciji razlomljenog dela, ovo povlači . Prema definiciji razlomljenog dela, ovo povlači 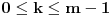 . .Sada dobijamo 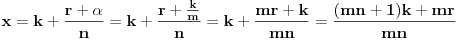 za za 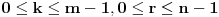 Proverimo sada jesu li neka dva rešenja jednaka: 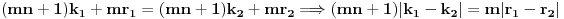 Ali 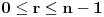 daje daje 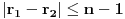 , stoga , stoga 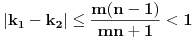 , pa je , pa je 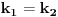 , što za uzvrat daje , što za uzvrat daje 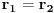 Prema tome, nijedna dva rešenja nisu jednaka, pa prosto možemo provući sume kroz izraz za  : :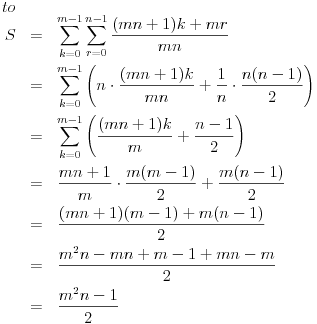 Dakle, moramo rešiti 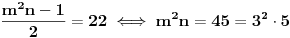 u prirodnim brojevima. Jedina rešenja očito su u prirodnim brojevima. Jedina rešenja očito su 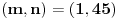 i i 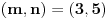 , a odgovarajuće jednačine glase , a odgovarajuće jednačine glase 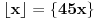 and and 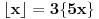 [ Cabo @ 10.05.2009. 16:15 ] @
Citat: Farenhajt: Pošto ni ovde, izgleda, nema interesenata, okačiću svoje rešenje. Ima interesenata, ali nema vremena. :) Pripremam Nacrtnu, kao što se da videti. Uzgred, da li bi možda ti mogao da mi odgovoriš da li dobro razmišljam u tom zadatku, ili se on može opštije rešiti? Niko mi nije odgovorio već neko vreme. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|