Evo ovako napamet, na prvu loptu.
Imaš sve njihove međusobne udaljenosti? Onda sortiraj sve te udaljenosti u rastućem nizu, od najmanjih ka najvećim. Onda lepo uzimaš prvu, pa prvu i drugu, pa prvu, drugu i treću, itd., tj. uzimaš n-torke tačaka i za svaku n-torku računaš prostor koje one ograničavaju. Onog trenutka kada taj prostor postane jednak datom (ili bar manji za datu n-torku ukoliko za (n+1)-orku premašuje), dobio si skup tačaka koje su najmanje udaljene jedna od drugih i ograničavaju zadati prostor, dakle gustinu (a koja je najveća jer smo uzeli tačke koje su najmanje udaljene jedne od drugih).

_{[Ovu poruku je menjao mokelet dana 02.05.2009. u 12:28 GMT+1]}

Ne znam jesam li ja pogrešno shvatio ili si ti loše objasnio šta ti treba, ali odmah mi je palo na pamet da opišeš sitan krug oko jedne jedine tačke. Time možeš da postigneš gustinu koliku god veliku hoćeš — što je krug sitniji, veća je gustina na njegovom području. E sad, kako ovo očito nije ono što si tražio, možeš li da objasniš šta se u ovom primeru ne uklapa?

OK, ocigledno sam pogresno objasnio... hajmo ovako:

- imam sve koordinate tacaka u prostoru, te sam na osnovu njih izracunao sve njihove uzajamne udaljenosti (konkretno preko 200 tacaka izadje preko 25.000 kombinacija odnosno uzajamnih udaljenosti)
- cilj je da pronadjem i ogranicim podrucje koje ima najvecu koncentraciju tacaka u datom prostoru. Evo jedan logican primjer npr. ako imam prostor 10 km^2 i unutar njega 100 razlicito rasporedjenih tacaka (stambeni objekti), trebam da omedjim prostor (unutar tih 10 km^2) koji iima najvecu naseljenost (gledajuci po broju stambenih objekata). Problem je sto taj prostor ne mora da bude pravilnog geometrijskog oblika poput kvadrata ili kruga. Ovo moram izracunati u Excelu, a ono sto imam su 3 kolone sa koordinatama (plus sto sam izracunao sve njihove uzajamne udaljenosti - ako nam ovo uopste treba!?)

- ono sto mi pada na pamet je da nadjem tacke gomilanja sva 3 niza podataka (x,y,z) i da ih onda ukrstim da bih nasao gomiliste u prostoru (sto ne znam uraditi u Excelu), pa da onda racunam udaljenosti ostalih tacaka od tog gomilista u prostoru i onda samo sortiram podatke i eliminisem sve one gdje udaljenost znacajno odstupa od neke uobicajene (kako da procjenim/izracunam tu uobicajenu udaljenost?), tako da na kraju ostanu samo relevantne tacke u prostoru koje bi omedjivale taj prostor sa najvecom koncentracijom/gustinom tacaka... Moze se reci da tema spada i pod matematiku i pod Excel...

_{[Ovu poruku je menjao nh11 dana 02.05.2009. u 14:57 GMT+1]}

Izleda se i dalje ne razumemo. Postoje li neki dodatni uslovi koje taj omeđeni prostor mora da ispunjava (tipa: da obuhvata bar određeni broj tačaka, da bude određene površine i sl.)? Ako ne postoje, važi ono što sam rekao u prošloj poruci. Pogledaj: gustina se računa kao broj tačaka na određenom prostoru podeljen s površinom tog prostora, je li tako? Ako uzmeš samo jednu tačku, i opišeš oko nje vrlo mali krug (proglasiš taj krug za omeđeni prostor), gustina će ti biti 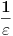, gde je površina tog kruga. E sad, kako je površina veoma mala, ispada da će gustina, 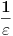, biti veoma velika. Kako planiraš da isključiš ovakve slučajeve?

Pa valjda moras dobiti konveksan poligon, jer u suprotnom ceo zadatak nema smisla.
Mada, čak i u slučaju konveksnog poligona može se desiti da imamo, recimo, tri tačke koje nisu kolinearne i koje su veoma blizu postavljene i onda one zadovoljavaju uslov najveće "gustoće".

@Marko: naravno da mora biti konveksan, ali ne mora biti pravi idealni krug, lopta sta vec...

@Bojan: naravno da mora postojati uslov, ali taj uslov treba da bude automatski generisan na osnovu vec postojecih i izracunatih medjusobnih udaljenosti - cilj je da se dobije najoptimalniji uslov, udaljenost od centra koja je najoptimalnija, koja nece uzimati ni previse ni premalo tacaka, uslov koji ce optimalno omedjiti to podrucje sa najvecom koncentracijom tacaka - da bih to dobio, onako cisto logikom moram da izracunam druge relativne udaljenosti pojedinih tacaka, a zato sam ih zapravo i racunao... gledaj to ovako: ako imas 2 sela sa po 100 kuca gusto razmjestenih, a izmedju njih imas 30 kuca, ali malo su udaljenije medjusobno nego sto je to slucaj unutar sela, optimalni postor ce obuhvatiti selo, ali bez tih rijetko razmjestenih kuca... spomenuti uslov je pola problema ovdje ako dobro vidim...

O kakvom "centru" govorimo onda?
Mnogo si uopšteno postavio problem. Moraćeš da fiksiraš neki uslov, inače se bojim da će problem biti teško rešiti u razumnom vremenu (slično problemu trgovačkog putnika). Možda grešim, nadam se da će me neko demantovati.

_{[Ovu poruku je menjao mokelet dana 02.05.2009. u 18:51 GMT+1]}

Problem je cisto prakticne prirode, naime imam zadatak da proracunam koji dio grada ima najvecu koncentraciju stambenih objekata, a sve sto imam je geo. duzina i sirina uz nadmorsku visinu svakog od objekata.
Moja ideja je bila da nadjem tacku gomilanja niza (nesto kao limes, samo sto ima konacno mnogo tacaka) za svaki od parametara (duzina, sirina i visina) te da ta gomilista ukrstim i da to predstavlja centar, dakle tacku oko koje se objekti gomilaju. Ako je ta tacka gomiliste u sve 3 dimenzije onda to znaci da je vecina stambenih objekata rasporedjena oko te tacke. Tad bih samo trebao da odredim udaljenosti od tog centra i nekom analizom tih vrijednosti da odredim koja od jnih predstavlja najoptimalniju udaljenost, te da odaberem sve tacke koje su unutar tog radiusa... Ako ova ideja ne valja u korijenu, dajte nesto drugo...

To ti je vrlo prosto. Izabereš neki neboder i plac na kome on stoji je najgušće naseljen. U tvom primeru sa selom, najgušće je naseljen prostor koji zauzima jedna kuća, a ne celo selo.

Imas dakle skup od n tacaka i njihove koordinate.
Racunas za svaku trojku, cetvorku, ..., n-torku tacaka da li grade konveksan poligon. Ako grade, onda racunas povrsinu koju te tacke omedjuju i zatim racunas gustinu (broj tacaka/povrsina). Na kraju izaberes najvecu gustinu i pripadajuci poligon koji ga omedjuje.
Ali kao sto rece Nedeljko, moras da postavis neki uslov koji je minimalan broj tacaka skupa koji trazimo. On ti je naveo primer kada jedna kuca na prostoru koji zauzima cini i najvecu gustinu. Ista je situacija i sa dve kuce, jer kako cemo onda racunai povrsinu izmedju njih? Zato sam ja krenuo od 3 tacke, ali i to je manjkavo jer se moze desiti da su tri kuce recimo jedna pored druge, i eto ti najvece gustine naseljenosti. Dakle, potreban ti je i taj uslov.

Ako imaš selo sa razbacanim kućama u kojima živi podjednako stanovnika, a ne
znaš gdje da gradiš crkvu ili školu, onda napravi ovakav kriterij:
Za svaku kuću nađi prosječnu udaljenost do svih preostalih kuća.Ona koja ima najmanju srednju udaljenost od ostalih je kandidat da se nađe odmah pored novosagrađene crkve.
Nevolja je ako su kuće razbacane kružno oko nekog polja.Tada bi morao napraviti
jednu fiktivnu kuću sa varijabilnim koordinatama.Pa onda u excelu mijenjaš te koordinate po nekoj odabranoj stopi i tražiš onaj optimum i dobiješ da je najbolje
napraviti crkvu i školu u centru onog kruga gdje ne živi niko.

Hm, možda da nađeš težište svih tačaka?

@nedeljko: dragi nedeljko pa necu valjda reci shefu da je najgusce naseljeno podrucje koje zauzima jedna kuca :)
@marko: ja ne znam ovo uraditi!
@milan: nisam siguran da li je to ovo sto meni treba? De neki primjer u Excelu sa npr. 10ak brojeva po sve 3 dimenzije...
@dusan: zasto? kako?

Hval aVam svima na trudu i vremenu, ali ja pojma nemam kako da ovo sve u Excelu odradim, ne znam sa VBA raditi, ima li funkcija? Dajte ljudi uzmite neku seriju od 10ak brojeva sta bilo, samo da skontam kako ovo cudo vise rijesiti, slomih se...

Tu bi mozda mogao pomoci Voronoi diagram.Ne znam pogledaj malo vidi da li se odatle moze nesto dobiti

Umesto težišta možda je bolje da napraviš nešto kao prostornu funkciju gustine raspodele verovatnoće, za slučaj da je grupisanje tačaka raspoređeno na više mesta.

OK ali kako? Dajte bar neki excelov fajl sa manjom serijom, npr. nekim uzorkom od 20 elemanata...

nh11:...pa necu valjda reci shefu da je najgusce naseljeno podrucje koje zauzima jedna kuca

Ovo je izgleda realan problem vezan za urbanizaciju nekog naselja?Ako je tako
onda bi ipak trebalo napraviti neki kriterij za određivanje granica najstrožije
urbane zone.Zasad imamo samo uslov da to bude najgušće naseljeni dio.
Usvojimo još nešto, naprimjer neka taj dio naselja sadrži minimalno 10% kuća,
ali ne više od 50%.(Ovi procenti neka budu varijabilni i ovisni o političkoj volji.)

Sada krenemo odabirati za svaku kuću onik 10 % najbližih kuća.I izračunavamo
površinu poligona (trokut po trokut pa sve saberemo).Nađemo omjere broja kuća i površina.Kandidat za "najgušći" je onaj poligon gdje je ovaj omjer najveći.

Nastavimo isti posao za broj kuća uvećan za jedan.
A onda za 2, 3 itd sve do 50% kuća.

Naći ćemo neki maksimum svih maksimuma za dati raspon i to je onda jedinstven poligon sa tačno definisanim kućama, i granicama kvarta.

Nije problem ni ako neke kuće imaju više stanova ili ako treba ubaciti u igru
i broj stanovnika za svaku kuću.

Može ovo sve ići u excelu, ali ipak bi morao ubaciti malo VB.Teško je računati
površinu poligona bez tog.

Jednostavno. Da li si familijaran sa jednodimenzionalnom funkcijom raspodele? Npr., ako ti je dato 1000 merenja neke slučajne promenljive tada tih 1000 rezultata rasporediš u nekih 10 ili 20 intervala širine dX i izračunaš frekvencije pojavljivanja u svakom od intervala. U tvom (trodimenzionalnom) slučaju interval ti je ustvari elementarna kocka dimezija dx*dy*dz. Dalje (nadam se) možeš sam?

Kada dobiješ funkciju gustine, lako ti je postaviti kriterijum: Zadaš neku vrednost (npr. 10 kuća po km kubnom) a rezultat će biti zatvorena površ u prostoru sa tom i većom gustinom.

Nisam hteo da te zavitlavam, već sam ti dao tačno rešenje one formulacije koju si dao, da bi shvatio zašto ti formulacija nije dobra. Matematika ti ne može dati ono što želiš, već samo rešenja uslova koje joj daš. Zato je matematičko modeliranje realnog problema bitno.

Ako bi nam izložio realan problem (to je ono zbog čega ti ova gustina treba, tj. tvoj urbanistički problem), možda bismo ga mi bolje modelirali i onda rešili.

Milan: koordinate urbane zone su zadate, i upravo treba da nadjem podrucja sa najvecom koncentracijom objekata unutar te zone... ipak s VBA nemam nikakvog iskustva... nisam programer niti matematicar... ali sta je tu je...

Dusane, kad pogledom na GIS kartu (ili na Google Earth) upravo vidim da je vecina objekata koncentrisana oko 3 tacke, dakle postoji 3 podrucja gdje su najvece koncentracije objekata. Sad ono sto ne znam je odrediti te tacke i koliko objekata ukljuciti u te 3 zone... Funkcija raspodjele, funkcija gustine - ne znam mnogo o tome :(
Raspored u grupe - da li trebam da ih prvo sortiram po redu pa onda rasporedjujem ili slucajnim izorkom, po mjestima gdje se trenutno nalaze? Takodje sve vrijednosti po sve 3 dimenzije su jedinstvene pa nema frekvencije pojavljivanja - radi se o geografskim koordinatama, ne mogu napraviti 2 kuce na istom mjestu!

Celo područje koje je od interesa ograničiš kvadrom:
(x1,x2) znači da gledaš samo opseg od x1 do x2 (širina)
(y1,y2) opseg od y1 do y2 (dužina)
(z1,z2) opseg od z1 do z2 (visina)

sva tri opsega podeliš na N delova i tako dobiješ N*N*N elementarnih kvadrova čije su ivice

(x2-x1)/N
(y2-y2)/N
(z2-z1)/N

Za svaki elementarni kvadar prebrojiš koliko ima kuća u njemu. Ako ti je važan i broj (o)soba (ili kvadaratura kuće) umesto broja kuća sabiraš odgovarajući ponder (npr. broj osoba). Ovaj zbir podeliš sa ukupnim brojem kuća (ili ukupnim ponderom). Dobijena vrednost ti je tražena gustina u tački koja je centar datog elementarnog kvadra. Ponavljajući ovu operaciju dobićeš funkciju F(x,y,z) (histogram) u N*N*N tačaka koju si tražio. Dalje ti je sve jednostavno.

To je zato što u toj razmeri ne vidiš jedan neboder, pa dodaješ uslov minimalne površine koju ta teritorija treba da ima.

Kažem ti, izloži nam taj urbanistički problem, pa da ga modeliramo i rešimo.