[ Janinka @ 03.05.2009. 22:35 ] @
|
| Ovako:Dat je integral (x*e^arctg[x])/sqrt[(1+x^2)^3](valjda sam tacno napisala).Resavala sam ga supstitucijom
arctg[x]=t pa je x=tg[x] i onda duplom parcijalnom integracijom dobila da je resenje
(e^t(sin[t]-cos[t])/2.Znam da je ovo tacno resenje,ali sada imam problem oko vracanja supstitucije-mozda je prosto,ali meni ne ide.Kako da dobijem tacno resenje? |
[ Farenhajt @ 03.05.2009. 23:20 ] @
Dakle, trebaju ti formule kojima se sinus i kosinus izražavaju preko tangensa.
Izvedi ih sama: počni od
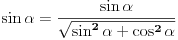
, pa i brojilac i imenilac podeli sa

.
Slično i za kosinus.
[ Janinka @ 03.05.2009. 23:49 ] @
Hvala,znam ja te formule,cudim se kako to nisam odmah shvatila,ali valjda me je umor "oborio" u ove kasne sate...
Sad se mucim sa jednim drugim integralom, int(e^(2x)*sin^2[x])dx) ostao mi je jos ovaj i ne ide...Probacu sutra,valjda cu se setiti.
Jos jednom,hvala...
Uspela sam da ga resim,nema potrebe da odgovarate...Ipak hvala Farenhajt-u...
[Ovu poruku je menjao Janinka dana 04.05.2009. u 01:36 GMT+1]
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.