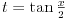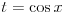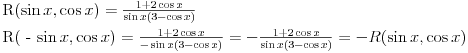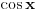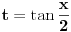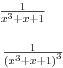Smena je „teška artiljerija“ koja skoro sigurno uvek „radi“; ona se koristi onda kada smena ne daje rezultate. Možeš pogledati, recimo, ovu datoteku (ignoriši deo o krivolinijskim integralima i sfernim koordinatama).

@igorpet:hvala, iako imam ove formule
@Cabo:znači iako teoretski po formuli mogu uvrstiti t=cosx, ako zapinjem znači koristim smjenu tgx/2=t.

Zaključak: Ako mi zapinje sa ovim specijalnim smjenama koristim smjenu tgx/2=t?

Da, smenu možeš uvek da koristiš, samo je problem što se njom dolazi do relativno komplikovanih izraza. Ako imaš određeni integral, onda moraš da paziš na monotonost. Sve to piše u teoriji. Recimo, ovo što je napisao igorpet piše kod Kadelburga u knjizi „Matematička analiza I“.

Ako su ti ove formule poznate onda bi trebalo da zakljucis da je smena t=cosx moguca u ovom konkretnom slucaju

Ova smena t=cosx je bolja zato sto t=tg(x/2) daje mnogo slozeniji integral za resavanje.

Da isprobamo ovo čudo ...

Da, kod neodređenih integrala se može primeniti svaka smena. Ali, iz toga što je pokretač teme postavio pitanje upotrebljivosti smene, može se zaključiti da je prvobitni problem bio određeni integral, u kom slučaju se smena ne može primeniti na svakom intervalu, već samo na onom na kom je monotona (a koliko se sećam tu je bilo još nekih dodatnih uslova diferencijabilnosti i neprekidnosti smene i/ili njenog prvog izvoda).

Smena se kao strogo monotona uvek može primeniti, jer se interval uvek može „iseckati“ na više podintervala, tako da se zaobiđe singularitet, pa se u slučaju nesvojstvenog integrala traži granična vrednost.

Cabo, nemam ja primedbi na tvoje opaske (mada ne moze se upotrebiti bas svaka smena), ja sam se samo drzao konkretno ovog primera i neodredjenih integrala. Iz postavke zadatka zakljucio sam da su u pitanju neodredjeni integrali. I dobro je sto si me dopunio i osvrnuo se i na odredjene integrale.

Izlazim malo iz konteksta ovog posta, ali Djoks jel mozes da testiras WolframAlpha (posto imas pristup) i za ove integrale:


Bas me interesuje da li su sada i oni resivi na Wolfram-u.
Nadam se da ti nece biti problem.
Gore navedeno resenje nije bas nesto optimizovano, pa me interesuje kakav postupak predlaze kad su "ozbiljniji" problemi u pitanju.

Daleko od toga - zadovoljstvo mi je da isprobavam ovu "mašineriju"...

Evo prvog integrala:



Drugog:



Sadržaj u skrolujućem dijelu nažalost nisam mogao uhvatiti u istoj slici, pa ga navodim u produžetku:



Nadam se da nećete zamjeriti zbog oblika izraza koji je morao proširiti tabelu van ekrana... :(

Hvala Djoks.
Ima napretka kod WolframAlpha, mada vrlo slabooooo (barem za ove komplikovanije probleme).
Od postupka nista, a i krajnje resenje je dato u vrlo diskutabilnom i neoptimizovanom obliku, mada malo je pribliznije nego do sada.
Ocekivao sam ja da ce malo vise unaprediti algoritam ... ali ... slabo.
Evo, npr. uradjen prvi primer "rucno":

Izgleda da jos jedno vreme necemo moci da se oslonimo na masine za komplikovanije probleme.
I necu vise da ovu temu skrecem, izvinite.

Jasno, hvala, poslao sam im kod primjera prvog integrala tvoj postupak (sliku) uz pitanje da li rezultat može biti jasniji i optimizovaniji. Ako i kada dobijem odgovor - poslaću ga na PM. :)

Zahvaljujem se na odgovorima i svima koji sudjeluju, prvotno me je zanimalo korištenje smjene, zadatak je zadan kao što je prikazan (neodređeni integral), al sad vidim koliko treba bit znanje da se uđe u malo dublju analizu problema, a još nisam toliko matematički pismen.:-)