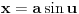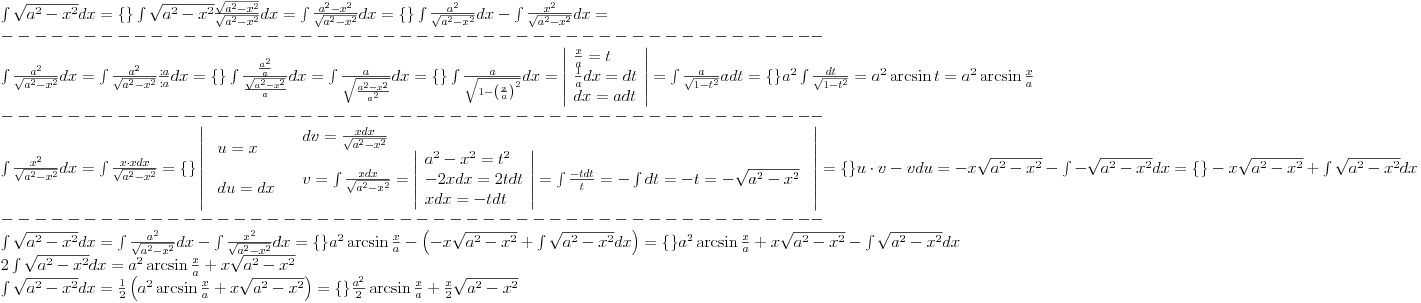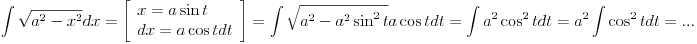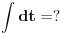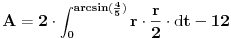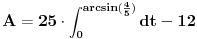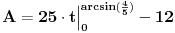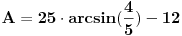[ gama-ray @ 11.05.2009. 14:52 ] @
| Naime imam sljedeći zadatak u bilježnici koji mi nije završen do kraja, a k tome ima mi jedna nejasnoća koju mi treba pojasnit nakon integracije dobija se sljedeći rezultat pa mi nije jasno kako,zadatak je na slj. slici: http://yfrog.com/6cdsc001382j |