[ boro1984 @ 13.05.2009. 11:15 ] @
| Da li neko mozda zna nacin na koji bi ovaj integral mogao da se resi? E da integral je od 0 do beskonacno. |
|
[ boro1984 @ 13.05.2009. 11:15 ] @
[ miki069 @ 13.05.2009. 12:14 ] @
X^4 + 1 = (X^2 + 1)^2 - 2*X^2 = razlika kvadrata....
[ boro1984 @ 13.05.2009. 12:33 ] @
Sve je to ok, resio sam ja integral kao neodredjeni i imam resenje u koje ne mogu da se ubace granice od 0 do beskonacno, jer dobijam +besk. i -besk.
[ NicholasMetropolis @ 13.05.2009. 12:58 ] @
Nešto si pogrešio. Diferenciraj tvoje rešenje i vidi da li dobijaš početni integral.
[ Nedeljko @ 13.05.2009. 13:09 ] @
Izraunaj određeni integral od a do b, pa onda pisti da a i be teže -oo i +oo tim redom.
[ Cabo @ 13.05.2009. 14:38 ] @
U principu (ne udubljujući se u ovaj konkretan problem) ne možeš da rešavaš određene integrale tako što rešiš neodređeni i onda samo „ubaciš“ granice. Može se desiti da smena nije monotona na intervalu integracije, i ne može da se primeni direktno, već se interval integracije mora podeliti na podintervale na kojima je smena monotona. Takođe, smena mora biti diferencijabilna na intervalu integracije.
Kod Merklea ima par primera kako se dobija pogrešno rešenje ako se ne pazi na monotonost. Možda ću kad dođem kući prekucati neki radi demonstracije, trenutno sam na fakultetu. [ NicholasMetropolis @ 13.05.2009. 16:28 ] @
[ igorpet @ 13.05.2009. 18:20 ] @
Citat: boro1984: Da li neko mozda zna nacin na koji bi ovaj integral mogao da se resi? E da integral je od 0 do beskonacno. Neprave integrale resavas kao odredjene integrale, pa zatim trazis limes. U principu to je napisano i u prethodnim postovima a ja samo da dodam: 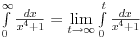 [ Cabo @ 13.05.2009. 22:11 ] @
Evo jednog lepog primera da ne može baš uvek da se radi
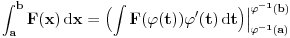 : :792. Da li je ispravan sledeći postupak: smenom 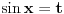 , , 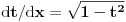 , dobijamo , dobijamo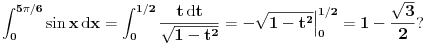 Rešenje. Postupak nije ispravan, jer se uzima da je 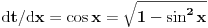 na celom domenu integracije, što nije tačno u ovom slučaju. Osnovna greška je u tome što funkcija na celom domenu integracije, što nije tačno u ovom slučaju. Osnovna greška je u tome što funkcija 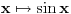 nije monotona na nije monotona na 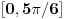 , pa se smena , pa se smena 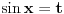 ne može upotrebiti. ne može upotrebiti.[Ovo je označeno „obrnutim uzvičnikom“, što predstavlja „klizav teren“ kod Merklea. Navedena smena može se uvesti na sledeći način: 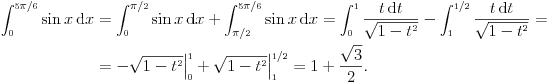 [ boro1984 @ 14.05.2009. 09:59 ] @
Ovo je konacno resenje neodredjenog integrala:
 znaci ovde ne mogu uvrstiti granice od 0 do besk.? [ Nedeljko @ 14.05.2009. 10:44 ] @
Citat: Cabo: Evo jednog lepog primera da ne može baš uvek da se radi 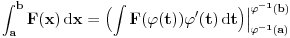 Upotrebio si oznaku 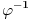 , odakle sledi da je , odakle sledi da je  inverzibilna funkcija, tako da nikakav primer sa neinverzibilnom funkcijom zapravo nije kontraprimer. inverzibilna funkcija, tako da nikakav primer sa neinverzibilnom funkcijom zapravo nije kontraprimer.U primeru koji si naveo se koristi arkus sinus, koji jednostavno nije inverzna funkcija sinusu, jer sinus zapravo i nema inverznu funkciju. Inverzna funkcija arkus sinusu je restrikcija sinusa na interval 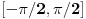 , a to nije podintegralna funkcija, jer se integracija vrši van tog domena. Smatram da je ovo najispravnije tumačenje tog primera. , a to nije podintegralna funkcija, jer se integracija vrši van tog domena. Smatram da je ovo najispravnije tumačenje tog primera.[ miki069 @ 14.05.2009. 13:14 ] @
Može + beskonačno pod limesom. Pre toga spoji ovu razliku logaritama u logaritam količnika. arctg od +beskonačno teži ka pi/2.
[ miki069 @ 14.05.2009. 13:19 ] @
Što smena mora da bude monotona na intervalu integracije?
Da bi imala inverznu f-ju. Nedeljkovo objašnjenje je maximalno korektno. [ Cabo @ 14.05.2009. 17:12 ] @
Citat: Nedeljko: Upotrebio si oznaku 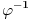 , odakle sledi da je , odakle sledi da je  inverzibilna funkcija, tako da nikakav primer sa neinverzibilnom funkcijom zapravo nije kontraprimer. inverzibilna funkcija, tako da nikakav primer sa neinverzibilnom funkcijom zapravo nije kontraprimer.Dobro. Onda 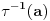 , gde je , gde je 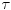 restrikcija od restrikcija od  na neki interval na neki interval 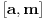 , i , i 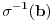 , gde je , gde je 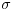 restrikcija od restrikcija od  na interval na interval 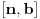 , gde je , gde je  , i , i 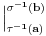 . Na to sam mislio. To je pogrešno. U redu? . Na to sam mislio. To je pogrešno. U redu?Citat: Nedeljko: U primeru koji si naveo se koristi arkus sinus, koji jednostavno nije inverzna funkcija sinusu, jer sinus zapravo i nema inverznu funkciju. Inverzna funkcija arkus sinusu je restrikcija sinusa na interval 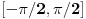 , a to nije podintegralna funkcija, jer se integracija vrši van tog domena. Smatram da je ovo najispravnije tumačenje tog primera. , a to nije podintegralna funkcija, jer se integracija vrši van tog domena. Smatram da je ovo najispravnije tumačenje tog primera.Sinus ima inverznu funkciju na poddomenu na kom je monoton, na primer na 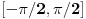 . Upravo i jeste poenta u tome da se uoči da podintegralna funkcija „šeta“, da nije monotona, pa se za dve vrednosti . Upravo i jeste poenta u tome da se uoči da podintegralna funkcija „šeta“, da nije monotona, pa se za dve vrednosti  -a može dobiti ista vrednost -a može dobiti ista vrednost  -a. -a.[Ovu poruku je menjao Cabo dana 14.05.2009. u 18:34 GMT+1] [ NicholasMetropolis @ 14.05.2009. 18:37 ] @
Citat: boro1984: znaci ovde ne mogu uvrstiti granice od 0 do besk.? Prepiši razliku logaritama kao logaritam količnika i videćeš da taj član u  postaje 0 tako da ti ostaju samo arkustangensi koji će ti dati po postaje 0 tako da ti ostaju samo arkustangensi koji će ti dati po 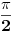 . .[ boro1984 @ 15.05.2009. 09:16 ] @
Hvala svima, integral je resen! :-)
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|