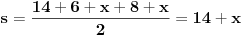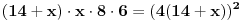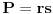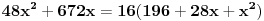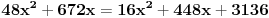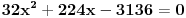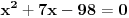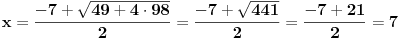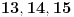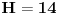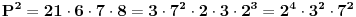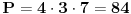[ semaaa @ 13.05.2009. 17:33 ] @
| evo zadatak: 'Osnova pravilne prizme je trougao poluprečnika upisane kružnice r=4 ,stranica a je dodirnom tačkom(sa kružnicom) podijeljena na odsječke dužine 6 i 8. Izračunati zapreminu V te prizme ako je visina prizme H jednaka srednjoj po veličini stranici trougla!' Pokušavao sam sa Heronovim obrazcem i povrsinom trougla preko poluobima...ali ono sto mi nije bas jasno jesu ustvari ti odsječci,imam neke predpostavke ali nisam siguran... Moze li neko uraditi pa objasniti??? (3 sam razred gimnazije) |