Puno hvala! :)

Evo mene opet...
Probao sam i ovako A = Table[Random[Integer, {-150, 150}], {j, 101}, {i, 101}] i napravi mi matricu, pa me zanima ima li kakve razlike između ta dva načina?

Izračunao sam trag, determinantu i svojstvene vrijednosti matrice, ima ih i kompleksnih i realnih, a sada bih pomoću funkcije Select trebao izdvojiti samo realne svojstvene vrijednosti.
Probao sam sa Select[Eigenvalues[N[A]], Reals], ali dobijem jedino

{}

:(

Nema razlike (osim u dužini zapisa), a još je i najprirodnije Table[Random[Integer, {-150, 150}], {101}, {101}] (tj. bez imenovanja brojačâ). Prošli put sam ponudio onu varijantu zato što na kompjuteru s kog sam pisao nije bilo Mathematice, a meni se sve nešto činilo da varijanta bez brojača nije radila u nekim starim verzijama — pa sam napisao ono što je bilo sigurno.

Reč Reals u Mathematici označava skup realnih brojeva, što znači da tvojom komandom proveravaš postoji li među sopstvenim vrednostima skup 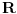— i logično je što dobiješ odgovor da ga nema tamo. Tebi u stvari treba selektovanje elemenata koji pripadaju dotičnom skupu, što postižeš komandom Select[Eigenvalues[N[A]], # ∊ Reals &].

Istina, baš :)

Nego, da pitam ja dalje :)
Nakon što sam našao svojstvene vektore sa Eigenvectors[N[A]], sad bih trebao izdvojiti samo svojstvene vektore pridružene realnim svojstvenim vrijednostima, koristeći Select, Map i Apply funkcije.

Gledao sam help file, i dok mi je Select više-manje jasan, Map i Apply mi uopće nisu jasni što rade oni zapravo :S

U tom slučaju je zgodnije da koristiš funkciju Eigensystem, čiji su rezultat parovi sopstvena vrednost — sopstveni vektor. Da bi izdvojio samo realne, upiši Select[Eigensystem[N[A]], #[[1]] ∊ Reals &].

uh, sudeći po naslovu, lagano ulazim u neki mathematica help topic :)

Tamo kada sam odredio sve svojstvene vrijednosti matrice...sada ih trebam prikazati kao točke u kompleksnoj ravnini.
Pretpostavljam da će to izgledati dosta... raspršeno, dok će na x-osi (osi realnog dijela kompleksnog broja) biti samo par točaka, jer od svih svojstvenih vrijednosti samo njih par je realno.

Koristim funkciju: ListPlot[Eigenvalues[N[A]], PlotRange -> All, PlotStyle -> PointSize[Large]], ali mi dobiveni graf i nije baš "neki" :/
Dobijem tek 9 točaka, a trebao bi ih imati daleko više. Zanimljivo mi je to da baš imam 9 realnih svojstvenih vrijednosti :)

Pa je pitanje - kako dobiti kompleksnu ravninu, odnosno kompleksni koordinatni sustav?

Možeš umesto kompleksnih brojeva posmatrati uređene parove koji se sastoje od realnog i imaginarnog dela zasebno, pa ih tako ucrtati. Komanda bi bila ListPlot[{Re[#], Im[#]} & /@ Eigenvalues[N[A]], PlotRange -> All, PlotStyle -> PointSize[Large]].

Odlično radi :)

Još par pitanja ;)

Crtanje kvadratne matrice, reda 20, koja ima sve elemente 0, osim glavne dijagonale koja ima random cjelobrojne elemente iz [-5,5], i dijagonale iznad nje koja ima bilo šta (osim samih nula).
Na tragu sam rješenja (barem mislim) sa:

DiagonalMatrix[{Table[Random[Integer, {-5, 5}]]}, 0, 20]
dobijem matricu reda 20, samo što mi se samo prvi element generira, ne i cijela glavna dijagonala.

Pretpostavljam da ću za popunjavanje ove dijagonale iznad glavne morati ovu 0 promijeniti u 1, što je kao neki offset?

Uh, polako. Ne znam šta će ti one vitičaste zagrade, to je prvi problem. A drugo, dvadesetica treba da ti bude brojač za Table, a ne za DiagonalMatrix.

Dobro si pretpostavio kako se popunjava dijagonala iznad glavne.

Vitičaste zagrade sam stavio jer sam iz Helpa skužio da DiagonalMatrix ide u obliku DiagonalMatrix[list,k], a list se unosi pomoću vitičastih zagrada :)
I onda mi je išla logika generiranja tablice unutar tih zagrada, pa da ti elementi zapravo budu članovi liste, ali sam previdio brojač :)

Ali uz tvoje savjete sad imam matricu koja na glavnoj dijagonali ima random [-5,5] - DiagonalMatrix[Table[Random[Integer, {-5, 5}], {20}], 0, 20] // MatrixForm

Inače, dijagonalu iznad glavne sam dobio sa DiagonalMatrix[Table[Random[Integer, {-5, 5}], {20}], 1, 20]+DiagonalMatrix[Table[Random[Integer, {-5, 5}], {19}], 1, 20], znači, smanjio sam brojač za 1, jer je 19 elemenata na toj dijagonali, ostavio isti raspon brojeva i sve to pomaknuo za 1.

Moćno :)

Dobro veče, evo mene još malo :)

Sad moram napraviti dvije matrice, A i B, prema slijedćim pravilima:
A matrica mora biti oblika (30,20) i ima random elemente iz skupa {-1,0,1}
B matrica je kvadratna matrica reda 20, koja na glavnoj dijagonali i dijagonali iznad nje ima random elemente iz [-5,5]

To sam izveo ovako:
A = Table[Random[Integer, {-1, 1}], {30}, {20}]
B = DiagonalMatrix[Table[Random[Integer, {-5, 5}], {20}], 0, 20] + DiagonalMatrix[Table[Random[Integer, {-5, 5}], {19}], 1, 20]

E sad, trebam generirati random matrice oblika AB i napraviti 70 iteracija, te ispisati te matrice i odrediti im rang.
To sam riješio pomoću While petlje - odnosno, u svakoj iteraciji generiram A matricu koju množim sa B matricom i ispisujem rezultat i rang te nove matrice
n = 1; While[n < 71, Print[MatrixForm[c = (Table[Random[Integer, {-1, 1}], {30}, {20}]).(DiagonalMatrix[Table[Random[Integer, {-5, 5}], {20}], 0, 20] + DiagonalMatrix[Table[Random[Integer, {-5, 5}], {19}], 1, 20])], " je rang matrice :)" MatrixRank[c]]; n++]

Nisam stavljao Print[MatrixForm[c=A.B]] jer sam skužio da mi onda izbaci iste matrice, jel...koje su već izgenerirane. Ovako im generira baš u petlji, u svakoj iteraciji po novu matricu.

I sad mi je zadatak od tih 70 matrica odabrati onu sa najmanjim rangom i odrediti joj jezgu i defekt. Za to dvoje ću se snaći, ali mene zanima jel postoji neka funkcija koja bi prošla kroz tih 70 matrica i odabrala onu sa najmanjim rangom, ili ja moram ručno skrolati i odabrati?

Napomenuo bih da se u zadatku kaže da ako ima više matrica sa najmanjim rangom (što je kod mene slučaj), onda nek se odabere po želji (naravno, od tih sa najmanjih rangom).

I još jedna stvar :)


Ovo mi vraća {}, prazni skup, što nebi smjelo bit :/